Skip to main content
\(\require{cancel}\newcommand\degree[0]{^{\circ}} \newcommand\Ccancel[2][black]{\renewcommand\CancelColor{\color{#1}}\cancel{#2}} \newcommand{\alert}[1]{\boldsymbol{\color{magenta}{#1}}} \newcommand{\blert}[1]{\boldsymbol{\color{blue}{#1}}} \newcommand{\bluetext}[1]{\color{blue}{#1}} \delimitershortfall-1sp \newcommand\abs[1]{\left|#1\right|} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

SectionCombining Transformations

Nearing the end of this chapter, we have now discussed several tranformations which can be performed on a function. Since we now have a solid grasp on each of these transformations, let's apply multiple transformations to a function and study the outcome.

SubsectionOrder Matters

Consider \(f(x)=(x-1)^2\text{.}\) We know from a previous section that the graph of \(f(x)\) is the graph of \(x^2\) shifted \(1\) unit to the right.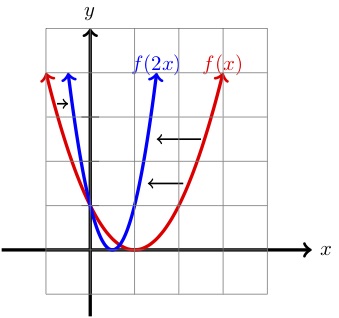

yHorizontal Compression
Figure275
As we know from the previous section, \(f(2x)\) is a horizontal compression by a factor of \(2 \text{.}\) However, here is where you need to be careful. When combining transformations, order matters.

The function \(f(2x)=(2x-1)^2\) should really be thought of as \(f(2x)=(2(x-\frac{1}{2}))^2\) and is the result of starting with \(x^2\) and applying

  1. horizontal compression by a factor of \(2 \)
  2. horizontal shift right by \(\frac{1}{2}\)

in this order.

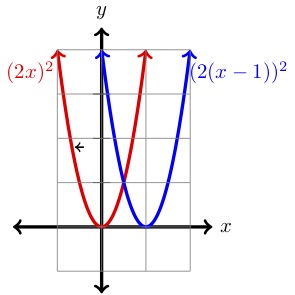
yHorizontal Compression
Figure276

SubsectionWhich Order to Use

As discussed thus far, in general, the order is important with transformations. However, if the transformations are vertical and horizontal changes then it does not matter whether the horizontal or vertical transformations are handled first. In general, we can follow the following guide:

Order of Transformations

Suppose that \(f(x)\) is our function we are applying transformations to. Once written in the form

\begin{equation*} a\cdot f\big(b\cdot (x+h)\big)+k \end{equation*}

the order of transformations is:

  1. horizontal stretch or compress by a factor of \(\abs{b}\) or \(\abs{\dfrac{1}{b}}\) (if \(b\lt 0\) then also reflect about \(y\)-axis)
  2. shift horizontally left/ right by \(\abs{h} \)
  3. vertically stretch or compress by a factor of \(\abs{a}\) or \(\abs{\dfrac{1}{a}}\) (if \(a\lt 0\) then also reflect about \(x\)-axis)
  4. shift vertically up/ down by \(\abs{k} \)
Example277

Describe the function

\begin{equation*} 5\cdot \Big(f(-3x-6)-1\Big) \end{equation*}

as a list of transformations done to \(f(x)\) in the appropriate order.

Solution

First, let's rewrite the function in the form given above: \begin{align*} 5\cdot \Big(f(-3x-6)-1\Big)\amp = 5f(-3x-6)-5 \ \ \text{we distributed in the 5}\\ \amp = 5f\big(-3(x+2)\big)-5 \ \ \text{we factored out the -3} \end{align*} Now that the function is written in the desired order, we may list off the transformations in the correct order using the order discussed above:

  1. horizontal compress by \(3\) and reflect about the \(y\)-axis
  2. shift horizontally left by \(2 \)
  3. vertically stretch by \(5\)
  4. shift vertically down by \(5 \)

SubsectionSupplemental Videos

SubsectionExercises