In this section, you will...
define polynomials and explore their characteristics
evaluate polynomials
perform the four basic operations on polynomials
SectionAlgebra of Polynomials
In the previous section, we defined functions and practiced using the compact function notation. In this section, we will explore a particularly useful kind of function.
Supplemental Videos
The main topics of this section are also presented in the following videos:
A polynomial is an expression made up of a single term or sum of terms with only one variable in which each exponent is a positive whole number. For example,
\begin{equation*}
2x^3, \hspace{.5cm} 8x^4-x^2+9, \hspace{.5cm} x^9, \hspace{.5cm} x+4
\end{equation*}
are all polynomials, while
\begin{equation*}
x^{-3}, \hspace{.5cm} 4x^{0.5}+2, \hspace{.5cm} \dfrac{1}{x^4}
\end{equation*}
are not polynomials. Polynomials define functions of the form
\begin{gather*}
f(x)=a_n x^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0.
\end{gather*}
Here \(a_n\) represents any real number and \(n\) represents any whole number. The degree of a polynomial with one variable is the largest exponent of all the terms. Typically, we arrange terms of polynomials in descending order based on their degree and classify them as follows:
\begin{align*}
\begin{aligned}
f(x)\amp =2 \ \alert{\text{ Constant function (degree }0\text{)}}\\
g(x)\amp = 3x+2 \ \alert{\text{ Linear function (degree }1\text{)}}\\
h(x)\amp = 4x^2+3x+2 \ \alert{\text{ Quadratic function (degree }2\text{)}}\\
p(x)\amp = 5x^3+4x^2+3x+2 \ \alert{\text{ Cubic function (degree }3\text{)}}
\end{aligned}
\end{align*}
In this course, we call any polynomial with degree higher than 3 an \(n\)th-degree polynomial. For example, if the degree is 4, we call it a fourth-degree polynomial; if the degree is 5, we call it a fifth-degree polynomial, and so on.
When a polynomial is arranged in descending order based on their degree, we call the first term of the sum the leading term, and the coefficient part of this term is called the leading coefficient.
Example132
Given \(f(x)=3x^2+5x+17\text{,}\) \(g(x)=15x^{24}+36x^{22}+17x^4+31\text{,}\) \(h(x)=11x^2+17x^3+121x\text{,}\) \(j(x)=5x^3+2x+4x^3+3x+5\text{,}\) and \(k(x)=25\text{,}\) state the degree, leading term, and leading coefficient of each polynomial.
Solution
Looking at \(f(x)\text{,}\) we see that the highest power of \(x\) is \(2\text{,}\) so the degree is \(2\text{.}\) The term with the highest degree is \(3x^2\text{,}\) meaning this is our leading term, and the coefficient of this term is \(3\text{,}\) which means this is our leading coefficient.
Looking at \(g(x)\text{,}\) we see that the highest power of \(x\) is \(24\text{,}\) so the degree is \(24\text{.}\) The term with the highest degree is \(15x^{24}\text{,}\) meaning this is our leading term, and the coefficient of this term is \(15\text{,}\) which means this is our leading coefficient.
Looking at \(h(x)\text{,}\) we see that the polynomial is not arranged in descending order of degree, so we will rearrange first.
\begin{equation*}
h(x)=17x^3+11x^2+121x
\end{equation*}
Now we see that the highest power of \(x\) is \(3\text{,}\) so the degree is \(3\text{.}\) The term with the highest degree is \(17x^{3}\text{,}\) meaning this is our leading term, and the coefficient of this term is \(17\text{,}\) which means this is our leading coefficient.
Looking at \(j(x)\text{,}\) we see that the polynomial is not arranged in descending order of degree, so we will rearrange first.
\begin{equation*}
j(x)=5x^3+4x^3+2x+3x+5=9x^3+5x+5
\end{equation*}
Now we see that the highest power of \(x\) is \(3\text{,}\) so the degree is \(3\text{.}\) The term with the highest degree is \(9x^{3}\text{,}\) meaning this is our leading term, and the coefficient of this term is \(9\text{,}\) which means this is our leading coefficient.
Looking at \(k(x)\text{,}\) we have just a constant. This is the same as \(k(x)=25\cdot 1=25x^0\text{,}\) so we see that the highest power of \(x\) is \(0\text{,}\) so the degree is \(0\text{.}\) The term with the highest degree is \(25x^0=25\text{,}\) meaning this is our leading term, and the coefficient of this term is \(25\text{,}\) which means this is our leading coefficient.
Example133
Given \(f(x)=x^2-8x+17\text{,}\) find \(f(2)\) and \(f(4)\text{.}\)
Solution
Replace each instance of \(x\) with the value given inside the parentheses.
\begin{equation*}
\begin{aligned}
f(\alert{2})\amp = (\alert{2})^2-8(\alert{2})+17\\
\amp =4-16+17\\
\amp =4+1\\
\amp =5
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
f(\alert{4})\amp = (\alert{4})^2-8(\alert{4})+17\\
\amp =16-32+17\\
\amp =-16+17\\
\amp =1
\end{aligned}
\end{equation*}
We can write \(f(2)=5\) and \(f(4)=1\text{.}\) Remember that \(f(x)=y\) and so we can interpret these results on the graph as follows:
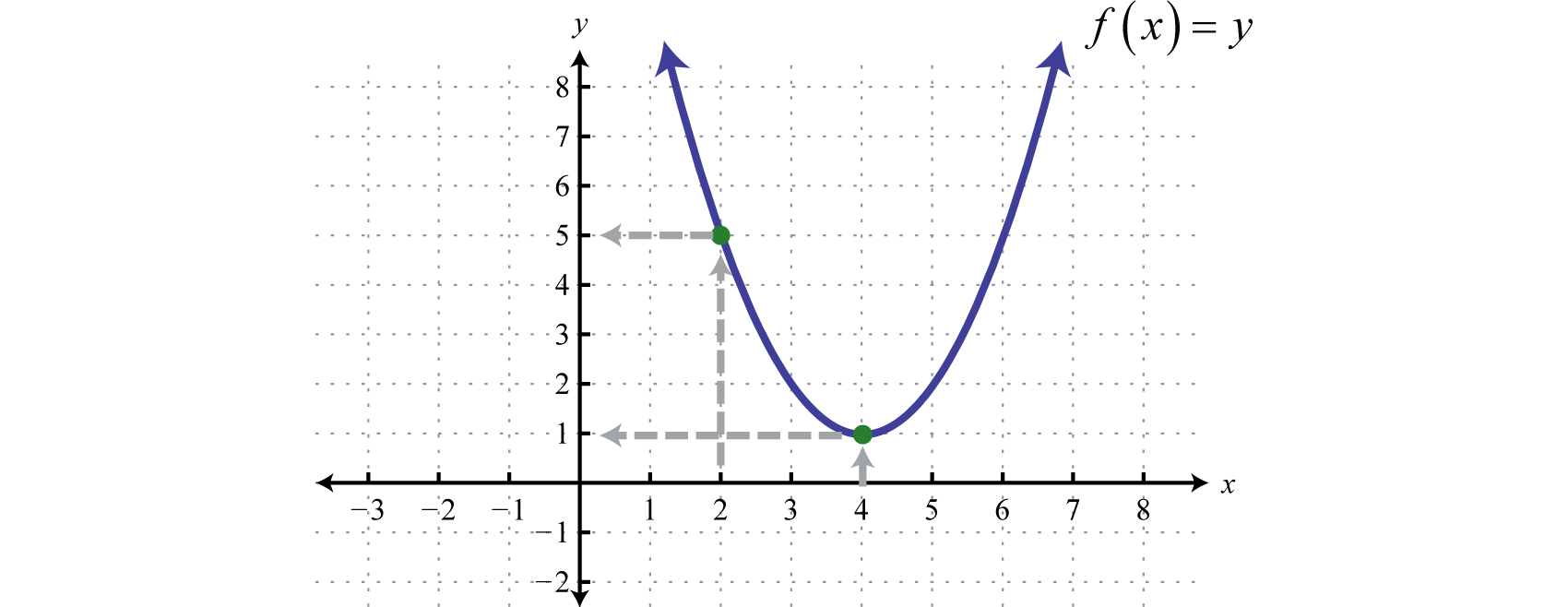
We find that \(f(2)=5\) and \(f(4)=1\text{.}\)
One useful application of polynomials appears in physics. The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following quadratic function:
\begin{gather*}
h(t)=-\frac{1}{2}gt^2+v_0t+s_0
\end{gather*}
With this formula, the height \(h(t)\) can be calculated at any given time \(t\) after the object is launched. The letter \(g\) represents acceleration due to gravity on the surface of the Earth, which is 32 feet per second squared (or, using metric units, \(g = 9.8\) meters per second squared). The parameter \(v_0\) pronounced v-naught, or sometimes v-zero, represents the initial velocity of the object. The parameter \(s_0\) represents the initial height from which the object was launched.
Example134
An object is launched from the ground at a speed of \(64\) feet per second. Write a function that models the height of the object and use it to calculate the object's height at \(1\) second and at \(3.5\) seconds.
Solution
We know that the acceleration due to gravity is \(g=32\) feet per second squared and we are given the initial velocity \(v_0=64\) feet per second. Since the object is launched from the ground, the initial height is \(s_0=0\) feet. Create the mathematical model by substituting these coefficients into the following formula:
\begin{equation*}
\begin{aligned}
h(t)\amp =-\frac{1}{2}gt^2+v_ot+s_0\\
h(t)\amp = -\frac{1}{2}(\alert{32})t^2+(\alert{64})t+\alert{0}\\
h(t)\amp = -16t^2+64t
\end{aligned}
\end{equation*}
Use this model to calculate the height of the object at \(1\) second and \(3.5\) seconds.
\begin{equation*}
\begin{aligned}
h(\alert{1})\amp = -16(\alert{1})^2+64(\alert{1})=-16+64=48\\
h(\alert{3.5})\amp = -16(\alert{3.5})^2+64(\alert{3.5})=-196+224=28
\end{aligned}
\end{equation*}
Our function is \(h(t)=-16t^2+64t\text{.}\) This tells us that at \(1\) second the object is at a height of \(48\) feet, and at \(3.5\) seconds it is at a height of \(28\) feet.
Example135
An object is dropped from a height of \(6\) meters. Write a function that models the height of the object and use it to calculate the object's height \(1\) second after it is dropped.
Solution
Our function is \(h(t)=-4.9t^2+6\text{.}\) Since
\begin{equation*}
\begin{aligned}
h(1) \amp= -4.9(1)^2+6 =1.1,
\end{aligned}
\end{equation*}
at \(1\) second the object is at a height of \(1.1\) meters.
SubsectionAdding and Subtracting Polynomials
On occasion a special notation is used to indicate addition and subtraction of functions. This mentioned here in the book so you have some exposure to the notation. The notation is as follows:
\begin{gather*}
\text{Addition of functions: }(f+g)(x)=f(x)+g(x)\\
\text{Subtraction of functions: }(f-g)(x)=f(x)-g(x).
\end{gather*}
When using function notation, be careful to group the entire function and add or subtract accordingly.
Example136
Given \(f(x)=x^3-5x-7\) and \(g(x)=3x^2+7x-2\text{,}\) find \(f(x)+g(x)\) and \(f(x)-g(x)\text{.}\)
Solution
The notation \(f(x)+g(x)\) indicates that we should add the given expressions.
\begin{equation*}
\begin{aligned}
f(x)+g(x)\amp = (x^3-5x-7)+(3x^2+7x-2)\\
\amp = x^3-5x-7+3x^2+7x-2\\
\amp = x^3+3x^2+2x-9
\end{aligned}
\end{equation*}
The notation \(f(x)-g(x)\) indicates that we should subtract the given expressions. When subtracting, the parentheses become very important. We can eliminate them after applying the distributive property.
\begin{equation*}
\begin{aligned}
f(x)-g(x) \amp = (x^3-5x-7)-(3x^2+7x-2)\\
\amp = x^3-5x-7-3x^2-7x+2\\
\amp = x^3-3x^2-12x-5
\end{aligned}
\end{equation*}
Our solutions are \(f(x)+g(x)=x^3+3x^2+2x-9\) and \(f(x)-g(x)= x^3-3x^2-12x-5\text{.}\)
We may be asked to evaluate the sum or difference of two functions. We have the option to first find the sum or difference in general and then use the resulting function to evaluate for the given variable, or evaluate each first and then find the sum or difference.
Example137
Evaluate \(f(3)-g(3)\) given \(f(x)=5x^2-x+4\) and \(g(x)=x^2+2x-3\text{.}\)
Solution
First, find \((f-g)(x)\text{.}\)
\begin{equation*}
\begin{aligned}
f(x)-g(x)\amp = (5x^2-x+4)-(x^2+2x-3)\\
\amp = 5x^2-x+4-x^2-2x+3\\
\amp = 4x^2-3x+7
\end{aligned}
\end{equation*}
Now we substitute \(3\) in for the variable \(x\text{.}\)
\begin{equation*}
\begin{aligned}
f(\alert{3})-g(\alert{3}) \amp = 4(\alert{3})^2-3(\alert{3})+7\\
\amp = 36-9+7\\
\amp = 34
\end{aligned}
\end{equation*}
Our solution is \(f(3)-g(3)=34\text{.}\)
Alternatively, we could have found \(f(3)\) and \(g(3)\) and then subtracted the results to obtain our answer.
Note: If multiple values are to be evaluated, it is best to find the sum or difference in general first and then use it to evaluate.
Example138
Given \(f(x)=x^3+x-8\) and \(g(x)=2x^2-x+9\text{,}\) evaluate \(f(2)+g(2)\) and \(f(-2)+g(-2)\text{.}\)
Solution
We will compute \(f(x)+g(x)\) on its own first.
\begin{equation*}
\begin{aligned}
f(x)+g(x) \amp= (x^3+x-8)+(2x^2-x+9)=x^3+2x^2+1
\end{aligned}
\end{equation*}
Using this, we see that
\begin{equation*}
\begin{aligned}
f(\alert{2})+g(\alert{2}) \amp= (\alert{2})^3+2(\alert{2})^2+1 \\
\amp= 8+2(4)+1 \\
\amp= 17
\end{aligned}
\end{equation*}
and
\begin{equation*}
\begin{aligned}
f(\alert{-2})+g(\alert{-2}) \amp= (\alert{-2})^3+2(\alert{-2})^2+1 \\
\amp= -8+2(4)+1 \\
\amp= 1
\end{aligned}
\end{equation*}
SubsectionMultiplying and Dividing Polynomials
The notation that is sometimes used to indicate multiplication and division of functions follows:
\begin{gather*}
\text{Multiplication of functions: }(f\cdot g)(x)=f(x)\cdot g(x)\\
\text{Division of functions: }\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}, \text{ where }g(x)\neq 0.
\end{gather*}
In this book we will simply consider multiplication notated by \(f(x)\cdot g(x)\) and division notated by \(\frac{f(x)}{g(x)}, \text{ where }g(x)\neq 0.\)
Example139
Given \(f(x)=15x^4-9x^3+6x^2\) and \(g(x)=3x^2\text{,}\) find \(f(x)\cdot g(x)\) and \(\frac{f(x)}{g(x)}\text{.}\)
Solution
Apply the distributive property and simplify.
\begin{equation*}
\begin{aligned}
f(x)\cdot g(x)\amp = (15x^4-9x^3+6x^2)(3x^2)\\
\amp = 15x^4\cdot\alert{3x^2}-9x^3\cdot \alert{3x^2}+6x^2\cdot\alert{3x^2}\\
\amp = 45x^6-27x^5+18x^4
\end{aligned}
\end{equation*}
For this quotient, assume \(x\neq 0\text{.}\)
\begin{equation*}
\begin{aligned}
\frac{f(x)}{g(x)}\amp = \frac{15x^4-9x^3+6x^2}{3x^2}\\
\amp = \frac{15x^4}{3x^2}-\frac{9x^3}{3x^2}+\frac{6x^2}{3x^2}\\
\amp = 5x^2-3x+2
\end{aligned}
\end{equation*}
Our solutions are \(f(x)\cdot g(x)=45x^6-27x^5+18x^4\) and \(\frac{f(x)}{g(x)}= 5x^2-3x+2\text{.}\)
Example140
Given \(f(x)=6x-5\) and \(g(x)=3x^2-2x-1\text{,}\) find \(f(0)\cdot g(0)\) and \(f(-1)\cdot g(-1)\text{.}\)
Solution
To find \(f(x)\cdot g(x)\text{,}\) we need to apply the distributive property multiple times. First, we distribute \(6x-5\) to each of the terms in \(g(x)\) and then distribute the terms to each of the \(6x-5\text{.}\)
\begin{equation*}
\begin{aligned}
f(x)\cdot g(x)\amp = (6x-5)(3x^2-2x-1) \\
\amp= (6x-5)(3x^2)-(6x-5)(2x)-(6x-5)(1) \\
\amp= (6x)(3x^2)-(5)(3x^2)-(6x)(2x)+(5)(2x)-(6x)(1)+(5)(1) \\
\amp= 18x^3-15x^2-12x^2+10x-6x+5 \\
\amp= 18x^3-27x^3+4x+5
\end{aligned}
\end{equation*}
Now we substitute \(0\) and \(-1\) in for the variable \(x\text{.}\)
\begin{equation*}
\begin{aligned}
f(0)\cdot g(0)\amp = 18(0)^3-27(0)^2+4(0)+5\\
\amp =5
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
f(-1)\cdot g(-1)\amp = 18(-1)^3-27(-1)^2+4(-1)+5\\
\amp = -18-27-4+5\\
\amp=-44
\end{aligned}
\end{equation*}
Our solutions are \(f(0)\cdot g(0)=5\) and \(f(-1)\cdot g(-1)=-44\text{.}\)
Example141
Given \(f(x)=x^3+x-8\) and \(g(x)=2x^2-x+9\text{,}\) find \(f(x)\cdot g(x)\text{.}\)
Solution
\begin{equation*}
\begin{aligned}
f(x)\cdot g(x) \amp= (x^3+x-8)(2x^2-x+9) \\
\amp= (x^3+x-8)(2x^2)-(x^3+x-8)(x)+(x^3+x-8)(9) \\
\amp= (x^3)(2x^2)+(x)(2x^2)-(8)(2x^2)-(x^3)(x)-(x)(x)\\
\amp \;\;\;\;\;\;\; +(8)(x)+(x^3)(9)+(x)(9)-(8)(9) \\
\amp= 2x^5+2x^3-16x^2-x^4-x^2+8x+9x^3+9x-72 \\
\amp= 2x^5-x^4+11x^3-17x^2+17x-72
\end{aligned}
\end{equation*}