In this section, you will...
review general factoring strategies
learn the zero factor principle
use the zero factor principle to solve polynomial equations
SectionSolving Polynomial Equations by Factoring
In the previous sections, we defined what it means to factor a polynomial and learned several factoring techniques. While factoring might seem like it's counterproductive to simplifying expressions, it does have useful applications. In this section, we will use factoring in order to solve polynomial equations.
Supplemental Videos
The main topics of this section are also presented in the following videos:
SubsectionReviewing General Factoring Strategies
We have learned various techniques for factoring polynomials with up to four terms. The challenge is to identify the type of polynomial and then decide which method to apply. The following outlines a general guideline for factoring polynomials:
Check for common factors. If the terms have common factors, then factor out the greatest common factor (GCF).
-
If there are no common factors, determine the number of terms in the polynomial.
If the polynomial has four terms, try to factor by grouping.
If it is a trinomial (3 terms), try using the \(ac\) method.
If it is a binomial (2 terms), check if it is a difference of squares.
Look for factors that can be factored further.
Check by multiplying.
If an expression has a GCF, then factor this out first. Doing so is often overlooked and typically results in factors that are easier to work with. Furthermore, look for the resulting factors to factor further; many factoring problems require more than one step. A polynomial is completely factored when none of the factors can be factored further.
If none of these techniques work, it might be the case that the polynomial is prime, or does not factor.
SubsectionSolving Polynomial Equations by Factoring
In this section, we will review a technique that can be used to solve certain polynomial equations. We begin with the zero factor principle:
\begin{gather*}
a\cdot b=0 \text{ if and only if }a=0\text{ or }b=0
\end{gather*}
The zero factor principle is true for any number of factors that make up an equation. In other words, if any product is equal to zero, then at least one of the variable factors must be equal to zero. If an expression is equal to zero and can be factored into linear factors, then we will be able to set each factor equal to zero and solve each equation.
Caution165
The zero factor principle is sometimes called the zero product property.
Example166
Solve \(2x(x-4)(5x+3)=0\text{.}\)
Solution
We set each variable factor equal to zero and solve.
\begin{equation*}
\begin{aligned}
2x\amp= 0\\
\frac{2x}{\alert{2}}\amp =\frac{0}{\alert{2}}\\
x\amp =0
\end{aligned}
\end{equation*}
OR
\begin{equation*}
\begin{aligned}
x-4\amp= 0\\
x\amp =4
\end{aligned}
\end{equation*}
OR
\begin{equation*}
\begin{aligned}
5x+3\amp= 0\\
5x\amp = -3\\
\frac{5x}{\alert{5}}\amp =\frac{-3}{\alert{5}}\\
x\amp = -\frac{3}{5}
\end{aligned}
\end{equation*}
To check that these are solutions we can substitute back into the original equation to see if we obtain a true statement. Note that each solution produces a zero factor.
The solutions are \(x=0,4,-\frac{3}{5}\text{.}\)
Of course, most equations will not be given in factored form.
Example167
Solve \(x^2-2x-35=0\text{.}\)
Solution
We will first factor \(x^2-2x-35\) using the \(ac\)-method.
Here \(a=1,\, b=-2\text{,}\) and \(c=-35\text{.}\)
\begin{equation*}
\begin{aligned}
ac=1(-35)=-35
\end{aligned}
\end{equation*}
Now we factor \(-35\text{,}\) and search for factors whose sum is \(-2\text{.}\)
\begin{equation*}
\begin{aligned}
-35\amp = -1(35)\\
\amp = -5(7)\\
\amp = \alert{-7(5)}\\
\end{aligned}
\end{equation*}
In this case, the sum of the factors \(-7\) and \(5\) equals the middle coefficient, \(-2\text{.}\) Therefore, \(-2x=5x-7x\text{,}\) and we can write
\begin{equation*}
\begin{aligned}
x^2-2x-35=x^2+5x-7x-35.
\end{aligned}
\end{equation*}
We factor the equivalent expression by grouping.
\begin{equation*}
\begin{aligned}
x^2-2x-35\amp =x^2+5x-7x-35\\
\amp = x(x+5)-7(x+5)\\
\amp = (x+5)(x-7)
\end{aligned}
\end{equation*}
Our factored form is \((x+5)(x-7)\text{.}\) Now we can use the zero factor principle to solve by setting each variable factor equal to zero.
\begin{equation*}
\begin{aligned}
x+5\amp= 0\\
x\amp =-5
\end{aligned}
\end{equation*}
OR
\begin{equation*}
\begin{aligned}
x-7\amp= 0\\
x\amp =7
\end{aligned}
\end{equation*}
To check that these are solutions we can substitute back into the original equation to see if we obtain a true statement. Note that each solution produces a zero factor.
The solutions are \(x=-5,7\text{.}\)
Example168
Solve \(x^2-8x-33=0\text{.}\)
Solution
We will first factor \(x^2-8x-33\) using the \(ac\)-method. We need two numbers that multiply to \(-33\) and add to \(-8\text{;}\) two such numbers are \(-11\) and \(3\text{,}\) we we can rewrite \(-8x\) as \(-11x+3x\text{.}\)
\begin{equation*}
\begin{aligned}
x^2-8x-33 \amp= x^2-11x+3x-33 \\
\amp= x(x-11)+3(x-11) \\
\amp= (x-11)(x+3)
\end{aligned}
\end{equation*}
Our factored form is \((x-11)(x+3)\text{.}\) Now we can use the zero factor principle to solve by setting each variable factor equal to zero.
\begin{equation*}
\begin{aligned}
x-11 \amp= 0 \\
x \amp= 11
\end{aligned}
\end{equation*}
OR
\begin{equation*}
\begin{aligned}
x+3 \amp= 0 \\
x \amp= -3
\end{aligned}
\end{equation*}
The solutions are \(x=11,-3\text{.}\)
Using the zero factor principle after factoring an expression that is equal to zero is the key to this technique. However, the expression may not be given equal to zero, and so there may be some preliminary steps before factoring. The steps required to solve by factoring are outlined in the following example.
Example169
Solve \(15x^2+3x-8=5x-7\text{.}\)
Solution
We will first express the equation in standard form, with zero on the right hand side.
\begin{equation*}
\begin{aligned}
15x^2+3x-8\amp =5x-7\\
15x^2-5x+3x-8+7\amp =0\\
15x^2-2x-1\amp =0
\end{aligned}
\end{equation*}
Now we can factor.
\begin{equation*}
\begin{aligned}
(3x-1)(5x+1)=0
\end{aligned}
\end{equation*}
Now we can use the zero factor principle to solve by setting each variable factor equal to zero.
\begin{equation*}
\begin{aligned}
3x-1\amp= 0\\
3x\amp =1\\
x\amp =\frac{1}{3}
\end{aligned}
\end{equation*}
OR
\begin{equation*}
\begin{aligned}
5x+1\amp= 0\\
5x\amp =-1\\
x\amp=-\frac{1}{5}
\end{aligned}
\end{equation*}
To check that these are solutions we can substitute back into the original equation to see if we obtain a true statement. Note that each solution produces a zero factor.
The solutions are \(x=\frac{1}{3},-\frac{1}{5}\text{.}\)
SubsectionFinding Roots of Functions
Any polynomial with one variable is a function and can be written in the form,
\begin{equation*}
f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0.
\end{equation*}
A root of a function is a value in the domain that results in zero. In other words, the roots occur when the function is equal to zero, \(f(x)=0\text{.}\)
Example170
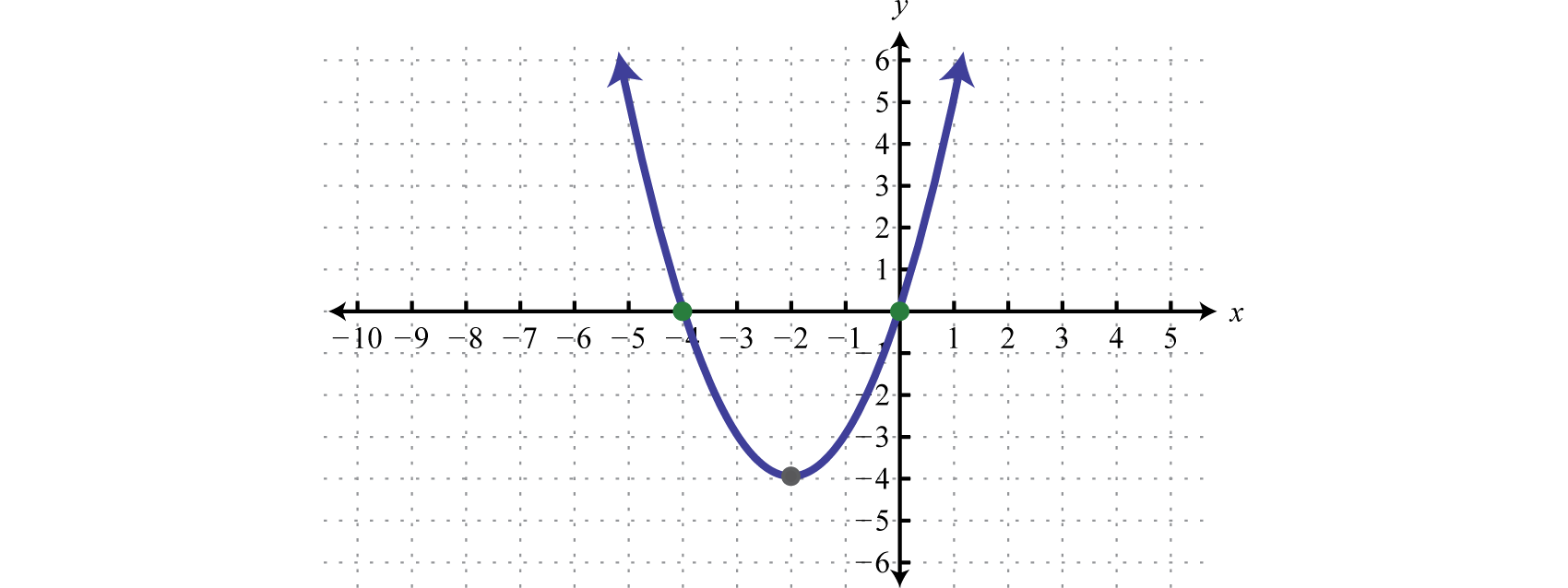
Find the roots of \(f(x)=(x+2)^2-4\text{.}\)
Solution
To find the roots we set the function equal to zero and solve.
\begin{equation*}
\begin{aligned}
f(x)\amp = 0\\
(x+2)^2-4\amp =0\\
x^2+4x+4-4\amp =0\\
x^2+4x\amp =0\\
x(x+4)\amp =0
\end{aligned}
\end{equation*}
Next, we set each factor equal to zero and solve.
\begin{equation*}
\begin{aligned}
x=0 \: \: \: \: \: \amp \text{ or }\amp x+4\amp =0\\
\amp\amp x\amp = -4
\end{aligned}
\end{equation*}
We can show that these \(x\)-values are roots by evaluating.
\begin{equation*}
\begin{aligned}
f(0)\amp = (0+2)^2-4\\
\amp =4-4\\
\amp =0
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
f(-4)\amp = (-4+2)^2-4\\
\amp =(-2)^2-4\\
\amp =4-4\\
\amp =0
\end{aligned}
\end{equation*}
The roots are \(0\) and \(-4\text{.}\)
If we graph the function in the previous example we will see that the roots correspond to the \(x\)-intercepts of the function. Here the function \(f\) is a basic parabola shifted 2 units to the left and 4 units down. Note: Shifts will be covered later but we include the description here so you can get used to the language.
Example171
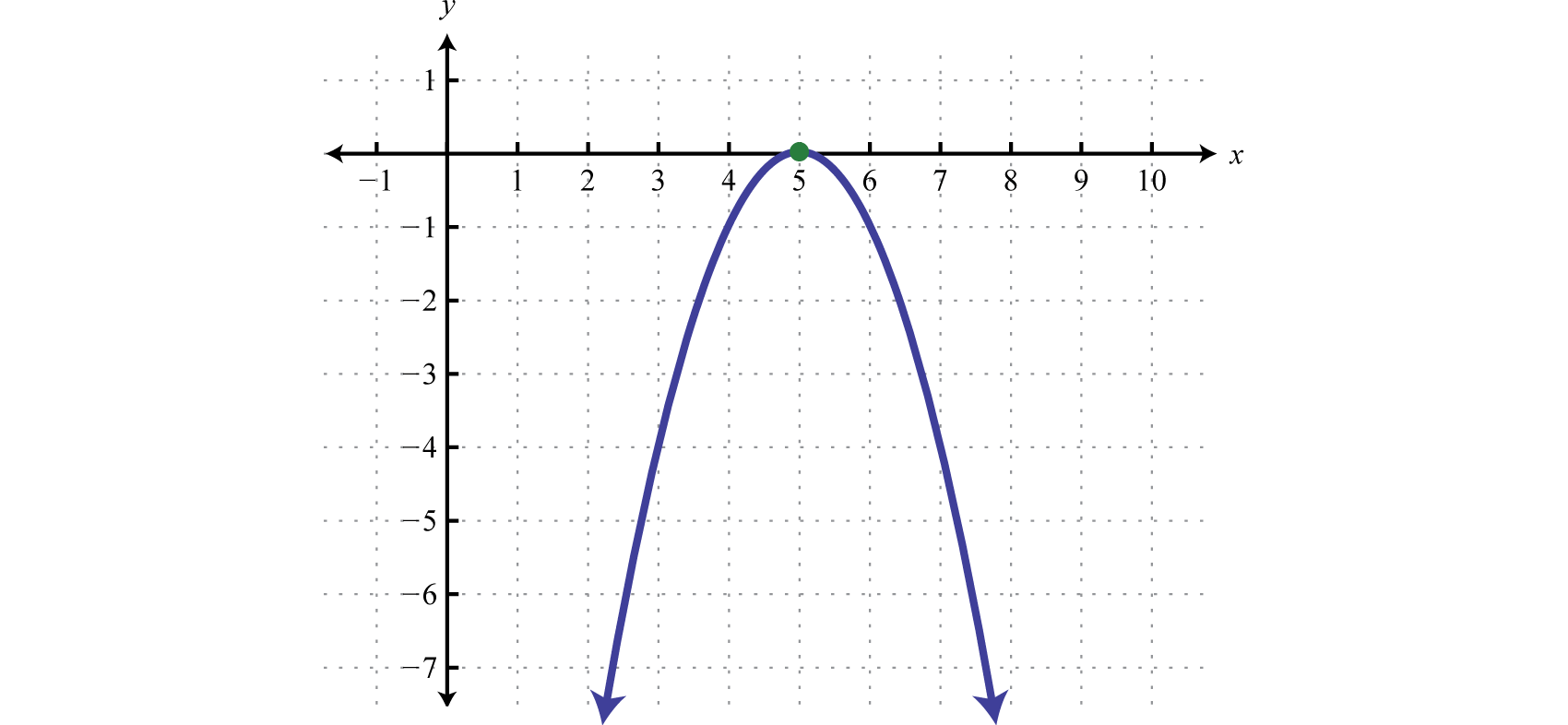
Find the roots of \(f(x)=-x^2+10x-25\text{.}\)
Solution
To find the roots we set the function equal to zero and solve.
\begin{equation*}
\begin{aligned}
f(x)\amp = 0\\
-x^2+10x-25\amp =0\\
-(x^2-10x+25)\amp =0\\
-(x-5)(x-5)\amp =0\\
\end{aligned}
\end{equation*}
Next, we set each variable factor equal to zero and solve.
\begin{equation*}
\begin{aligned}
x-5\amp=0\: \: \: \: \: \amp \text{ or }\: \: \: \: \: x-5\amp =0\\
x\amp =5\amp x\amp = 5.
\end{aligned}
\end{equation*}
A solution that is repeated twice is called a double root. The double root is \(5\text{.}\)
The previous example shows that a function of degree \(2\) can have one root. From the factoring step, we see that the function can be written
\begin{equation*}
f(x)=-(x-5)^2.
\end{equation*}
As we see below, the vertex on the graph is the \(x\)-intercept, illustrating the fact that there is only one root.
Exercise172
Solve \((6x-5)(x+7)=0\text{.}\)
Solution
The solutions are \(x=\frac{5}{6},/, -7\text{.}\)
Exercise173
Solve \((6x+1)(x+1)=6\text{.}\)
Solution
The solutions are \(x=-\frac{5}{3},/, \frac{1}{2}\text{.}\)
Exercise174
Solve \(4x^2+5x-5=15(3-2x)\text{.}\)
Solution
The solutions are \(x=\frac{5}{4},/, -10\text{.}\)
Example175
Assuming dry road conditions and average reaction times, the safe stopping distance in feet is given by \(d(x)=\frac{1}{20}x^2+x\text{,}\) where \(x\) represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in \(40\) feet.
Solution
We are asked to find the speed \(x\) where the safe stopping distance is \(d(x)=40\) feet.
\begin{equation*}
\begin{aligned}
d(x)\amp = 40\\
\frac{1}{20}x^2+x\amp =40
\end{aligned}
\end{equation*}
To solve for \(x\text{,}\) we rewrite the resulting equation in standard form. In this case, we will first multiply both sides by \(20\) to clear the fraction.
\begin{equation*}
\begin{aligned}
\alert{20}\left(\frac{1}{20}x^2+x\right)\amp =\alert{20}(40)\\
x^2+20x\amp = 800\\
x^2+20x-800\amp =0
\end{aligned}
\end{equation*}
Next, we factor and then set each factor equal to zero.
\begin{equation*}
\begin{aligned}
x^2+20x-800\amp =0\\
(x+40)(x-20)\amp =0
\end{aligned}
\end{equation*}
This means
\begin{equation*}
\begin{aligned}
x+40\amp =0 \: \: \: \: \: \amp \text{ or }\amp x-20\amp =0\\
x\amp =-40\amp\amp x\amp =20.
\end{aligned}
\end{equation*}
Since the negative answer does not make sense in the context of this problem, we consider \(x=20\) miles per hour to be the only solution.