Skip to main content
\(\require{cancel}\newcommand\degree[0]{^{\circ}} \newcommand\Ccancel[2][black]{\renewcommand\CancelColor{\color{#1}}\cancel{#2}} \newcommand{\alert}[1]{\boldsymbol{\color{magenta}{#1}}} \newcommand{\blert}[1]{\boldsymbol{\color{blue}{#1}}} \newcommand{\bluetext}[1]{\color{blue}{#1}} \delimitershortfall-1sp \newcommand\abs[1]{\left|#1\right|} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

SectionForms of a Line

Up to this point, we have explored several properties of linear equations and their graphs, such as how to graph lines, finding the intercepts of lines, and finding the slope. In this section, we will now work backwards and write equations of lines given certain properties.

In this section, you will...

  • learn two forms of linear equations: the slope-intercept form and the point-slope form

  • write an equation for a linear equation given

    • the slope of a line and its \(y\)-intercept

    • the slope of a line and any point on that line

    • any two points on the line

    • the graph of the equation

  • graph linear equations in point-slope and slope-intercept form

SubsectionSlope-Intercept Form

Slope-Intercept Form

The form of a linear equation that you're probably most famililar with is called the slope-intercept form, which looks like

\begin{equation*} y=mx+b. \end{equation*}

If a linear equation is in this form, then \(m\text{,}\) the coefficient in front of \(x\text{,}\) is the slope of the line, and \(b\text{,}\) the constant term, corresponds to the \(y\)-intercept of \((0,b)\text{.}\)

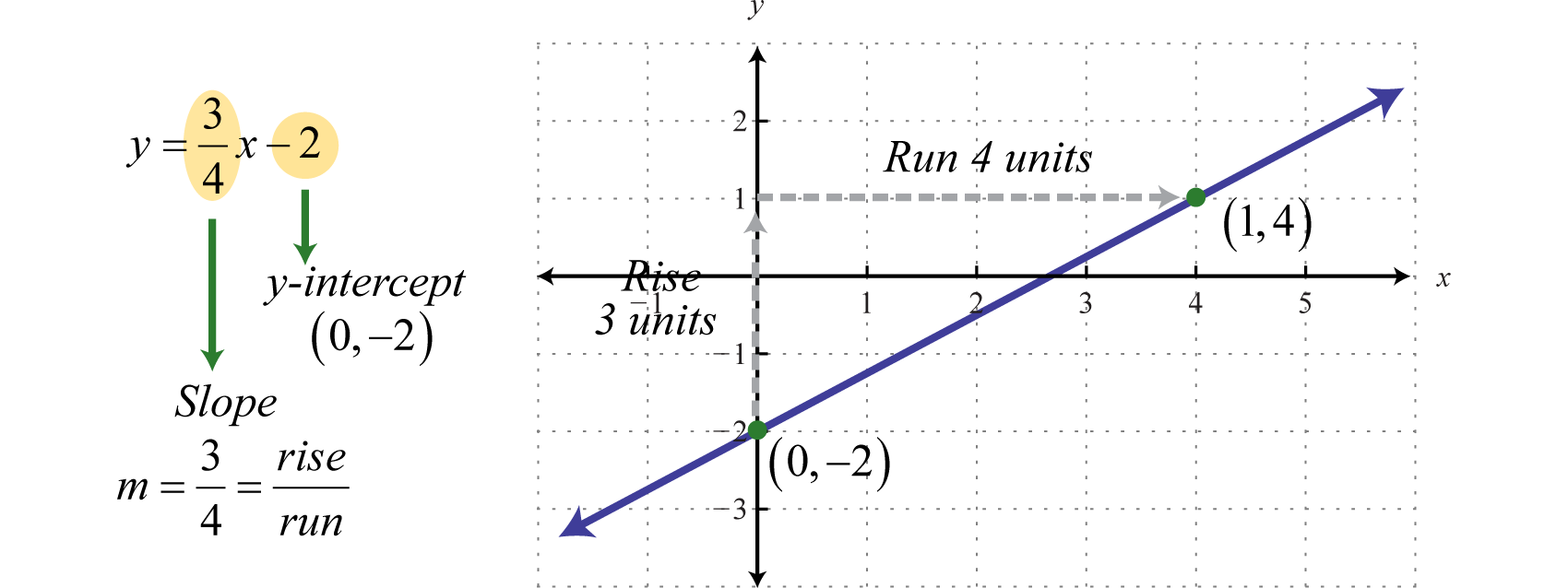
For example, suppose we're given the linear equation \(3x-4y=8\text{.}\) Solving for \(y\text{,}\) we have

\begin{align*} 3x-4y\amp =8\\ -4y\amp = -3x+8\\ y\amp =\frac{-3x+8}{-4}\\ y\amp = \frac{-3x}{-4}+\frac{8}{-4}\\ y\amp = \frac{3}{4}x-2\text{.} \end{align*}

From here, we can immediately see that the slope of this line is \(\frac{3}{4}\) and the \(y\)-intercept is at \((0,-2)\text{.}\) With this information, we can easily graph this line: we can first plot the \(y\)-intercept at \((0,-2)\text{,}\) and then use the slope to plot another point by going up \(3\) and over to the right \(4\text{.}\)

Quadrants of the Plane

Example85

Put the linear equation \(3y+5x=18\) into slope-intercept form. Graph this equation, and identify the \(x\)-intercept.

Solution

To put this equation into slope-intercept form, we need to solve for \(y\text{:}\)

\begin{equation*} \begin{aligned} 3y + 5x \amp= 18 \\ 3y \amp= -5x + 18 \\ y \amp= -\frac{5}{3}x + 6 \end{aligned} \end{equation*}

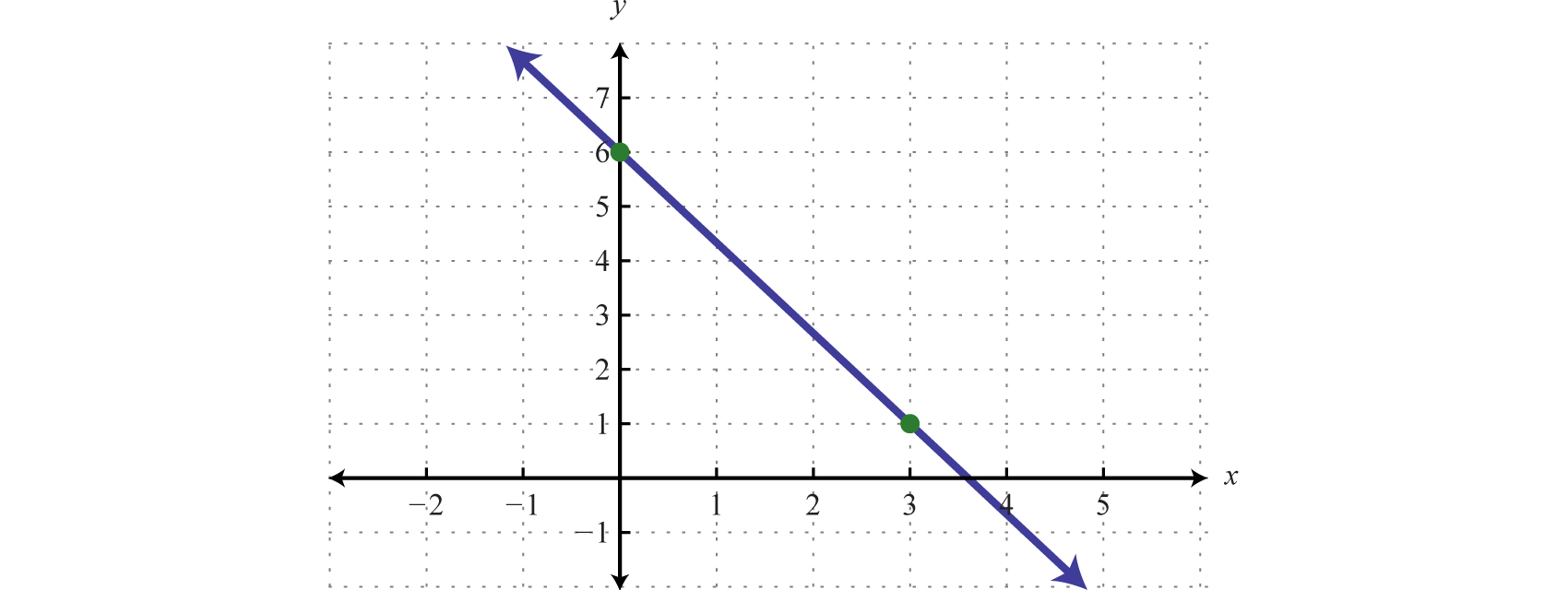
From here, we see that the slope is \(-\frac{5}{3}\) and the \(y\)-intercept is \((0,6)\text{.}\) To graph this equation, we first plot the \(y\)-intercept. Using the fact that

\begin{equation*} m=-\dfrac{5}{3}=\dfrac{-5}{3}=\dfrac{\text{rise}}{\text{run}}, \end{equation*}

we can find another point by starting from the \(y\)-intercept and moving down \(5\) units and right \(3\) units. Drawing the line passing through these two points, we get the line for this equation.

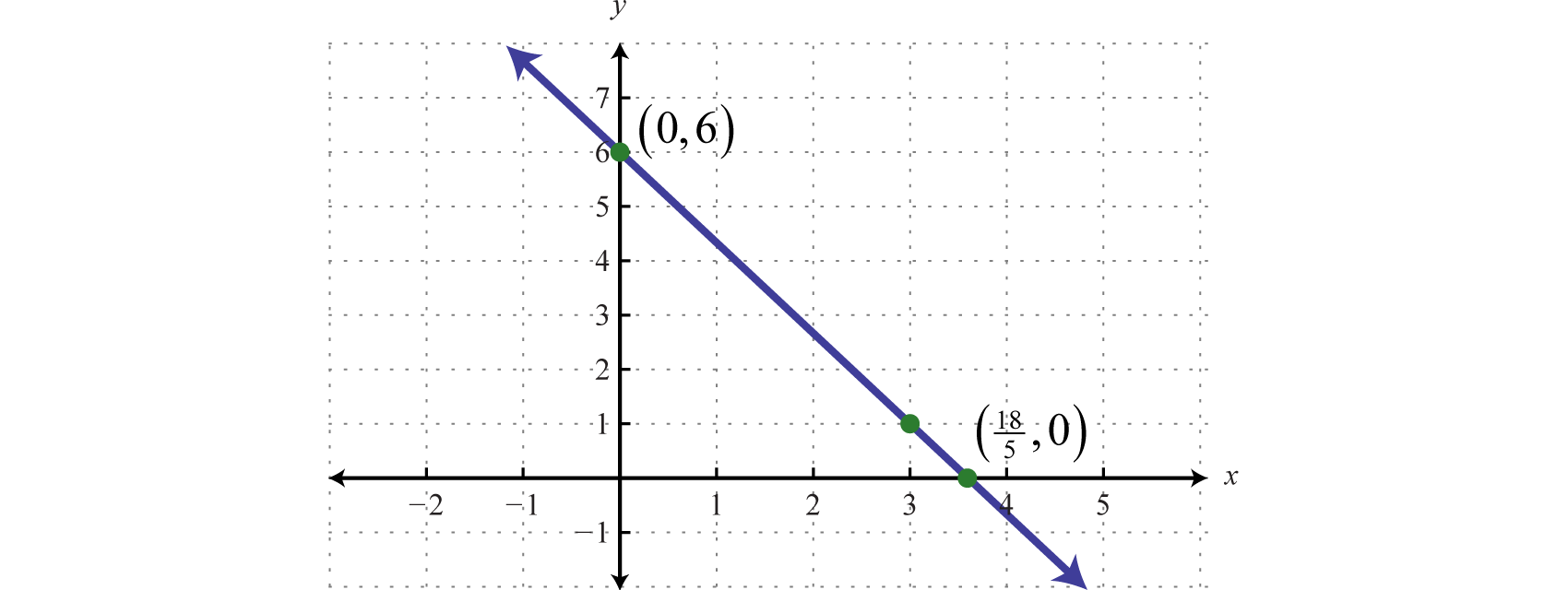
Quadrants of the Plane

To determine the \(x\)-intercept, we substitute \(y=0\text{:}\)

\begin{equation*} \begin{aligned} 3(\alert{0}) + 5x \amp = 18 \\ 5x \amp= 18 \\ x \amp= \frac{18}{5} \end{aligned} \end{equation*}

Therefore, the \(x\)-intercept is \(\left(\frac{18}{5},0\right)\text{.}\) The general rule is to label all important points that cannot be clearly read from the graph.

Quadrants of the Plane

Example86

Write a linear equation that defines the graph below, and find the \(x\)-intercept of the graph.

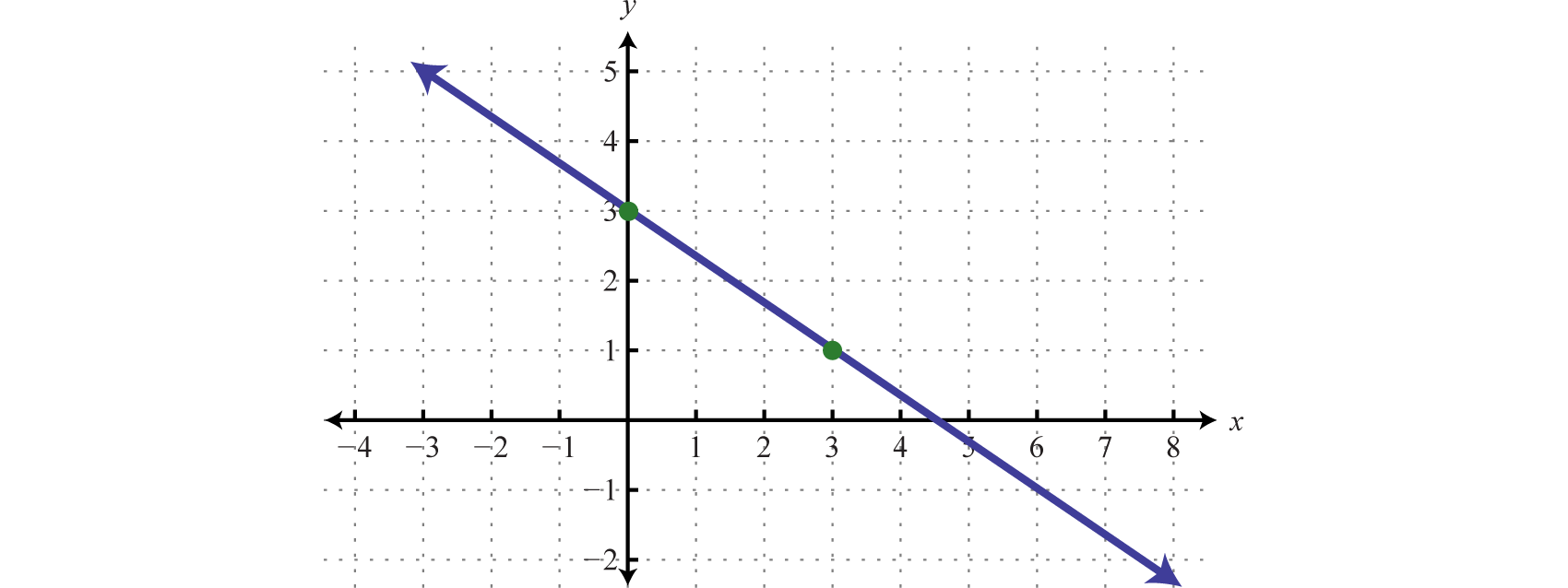
Solution

Consider the two points marked on the graph, \((0,3)\) and \((3,1)\text{.}\) From these points, we see that the slope is

\begin{equation*} m=\dfrac{\text{rise}}{\text{run}}=\dfrac{-2}{3} \end{equation*}

In addition, the \(y\)-intercept is \((0, 3)\) and thus \(b=3.\)Putting these together, we can write an equation in slope-intercept form:

\begin{equation*} y=-\dfrac{2}{3}x+3 \end{equation*}

To find the \(x\)-intercept of the graph, we substitute \(y=0\) and solve for \(x\text{:}\)

\begin{equation*} \begin{aligned} \alert{0} \amp= -\dfrac{2}{3}x+3 \\ \dfrac{2}{3}x \amp= 3 \\ x \amp= 3\cdot\dfrac{3}{2} \\ x\amp= \dfrac{9}{2} \end{aligned} \end{equation*}

Thus the \(x\)-intercept is given by \(\left(\frac{9}{2},0\right)\text{.}\)

SubsectionPoint-Slope Form

The slope-intercept form of a line is perhaps the simplest form, but it has its limitations. For example, suppose we wanted to write an equation for the following line.

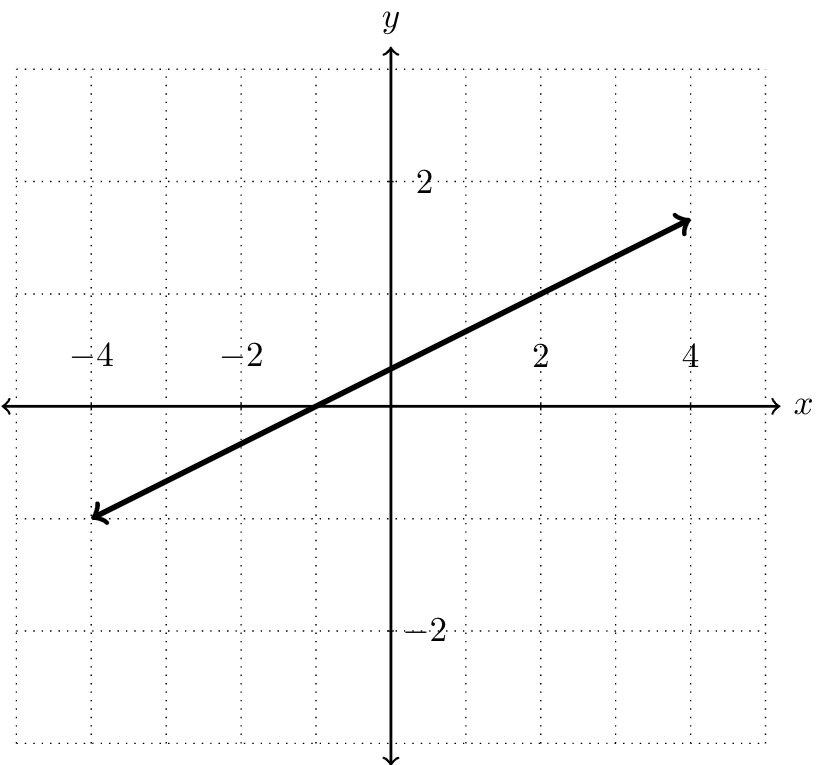
While we can certainly find the slope of this line, the \(y\)-intercept is not immediately clear. In cases like this where the \(y\)-intercept is not known, we can use the point-slope form of a line.

As the name suggests, point-slope form is useful when we know the slope and one point on a line. Suppose the slope of a line is \(m\) and we have a point \((x_1,y_1)\text{.}\) Let \((x,y)\) be a variable point. Then using the slope formula and rearranging, we have

\begin{equation*} \begin{aligned} m \amp= \dfrac{y-y_1}{x-x_1} \\ m(x-x_1) \amp = y - y_1 \end{aligned} \end{equation*}

Therefore, the equation of a line with a slope of \(m\) through the point \((x_1,y_1)\) can be written in point-slope form:

\begin{equation*} y-y_1=m(x-x_1) \end{equation*}

Let's return to the graph above. On the graph, we can identify two points, \((-1,0)\) and \((2,1)\text{.}\) These two points give us a slope of \(m=\frac{1}{3}\text{.}\) Next, we can use either point to write an equation for this line. Using \((x_1,y_1)=(-1,0)\text{,}\) we get an equation of

\begin{equation*} y-0=\dfrac{1}{3}(x-(-1)) \end{equation*}

Using \((x_1,y_1)=(2,1)\text{,}\) we get

\begin{equation*} y-1=\dfrac{1}{3}(x-2) \end{equation*}

It is not obvious that these are actually the same line; to verify this, we can simplify them both into slope-intercept form.

\begin{equation*} \begin{aligned} y-0 \amp= \dfrac{1}{3}(x-(-1)) \\ y \amp= \dfrac{1}{3}(x+1) \\ y \amp= \dfrac{1}{3}x+\dfrac{1}{3} \\ \\ y-1 \amp= \dfrac{1}{3}(x-2) \\ y-1 \amp= \dfrac{1}{3}x - \dfrac{2}{3} \\ y \amp= \dfrac{1}{3}x + \dfrac{1}{3} \end{aligned} \end{equation*}
Point-Slope Form

The point-slope form looks like

\begin{equation*} y-y_1=m(x-x_1) \end{equation*}

where \(m\) is the slope and \((x_1,y_1)\) is any point on the line. Sometimes, it is helpful to rewrite the formula as

\begin{equation*} y=y_1+m(x-x_1). \end{equation*}
Note87

Unless a problem specifically instructs you too, it's not necessary to rearrage and simplify the equations into slope-intercept form. In the previous example, it was only done to verify that the equation does not depend on which point you choose.

Example88

Write an equation for the line passing through the point \((3,6)\) and \((-2,5)\text{.}\)

Solution

First, we compute the slope:

\begin{equation*} m=\dfrac{6-5}{3-(-2)}=\dfrac{1}{5} \end{equation*}

Next, we use either point to construct an equation in point-slope form. It does not matter which point we choose. Using \((3,6)\text{,}\) we have

\begin{equation*} y-6=\dfrac{1}{5}(x-3) \end{equation*}
Example89

Write an equation that defines the following graph.

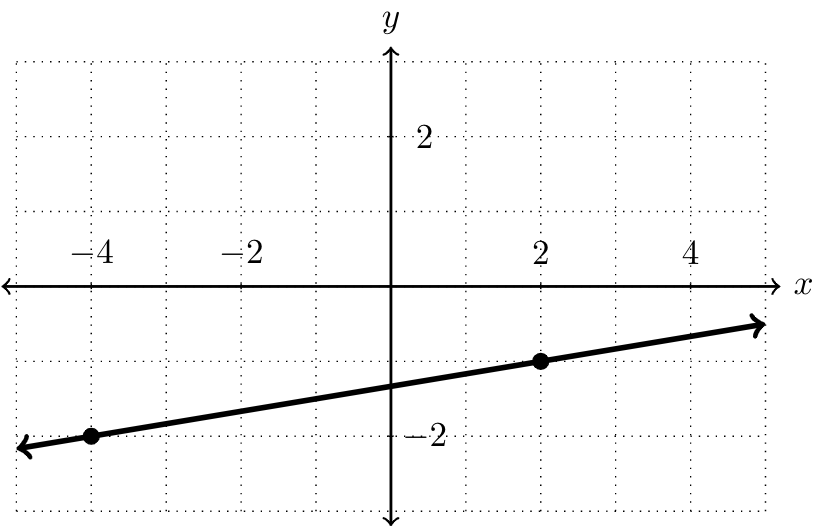
Solution

From the two marked points on the graph, we see that the slope is

\begin{equation*} m=\dfrac{\text{rise}}{\text{run}}=\dfrac{1}{6} \end{equation*}

Next, we use either point to construct an equation in point-slope form. Using \((-4,-2)\text{,}\) we have

\begin{equation*} \begin{aligned} y-(-2) \amp= \dfrac{1}{6}(x-(-4)) \\ y+2 \amp= \dfrac{1}{6}(x+4) \end{aligned} \end{equation*}

SubsectionExercises