Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionHorizontal Stretches and Compressions
In the previous section we discussed the result of multiplying the output of the function by a constant value. However, what happens when we multiply the input of the function? To explore this idea, we look at the graphs of
\begin{equation*}
f(x)=(x-1)^2 \text{, } ~f(2x)=(2x-1)^2\ \text{ ,and } ~f\left(\dfrac{1}{2}x\right)=\left(\dfrac{1}{2}x-1\right)^2
\end{equation*}
and discuss how they are related.
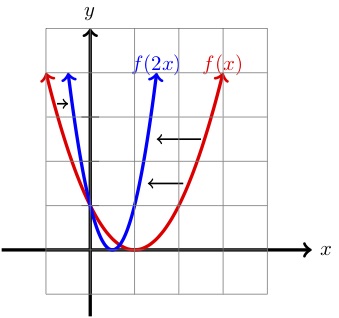
| \(x\) | \(y=f(x)\) | \(y=f(2x)\) |
| \(-1\) | \(4\) | \(8\) |
| \(-.5\) | \(2.25\) | \(4\) |
| \(0\) | \(1\) | \(1\) |
| \(.5\) | \(.25\) | \(0\) |
| \(1\) | \(0\) | \(1\) |
| \(2\) | \(1\) | \(9\) |
As we can see above, compared to the graph of \(f(x)\text{,}\) the graph of \(f(2x) \) is compressed horizontally by a factor of \(2 \text{.}\) Effectively, if we are given a point \((x,y) \) on the graph of \(f(x) \) then \(\left(\dfrac{1}{2}x,y\right) \) is a point on the graph of \(f(2x)\text{.}\)
Looking at the table above we can verify this for a few points. For example, the point \((2,1)\) is on the graph of \(f(x)\text{.}\) Then
\begin{equation*}
\left(\dfrac{1}{2}(2),1\right)=(1,1)
\end{equation*}
is a point on the graph \(f(2x)\text{.}\)
Horizontal Stretch
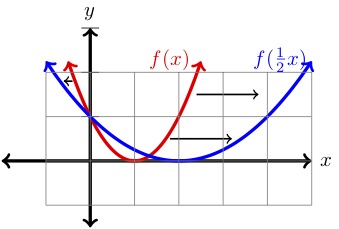
| \(x\) | \(y=f(x)\) | \(y=f\left(\dfrac{1}{2}x\right)\) |
| \(-1\) | \(4\) | \(2.25\) |
| \(0\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(.25\) |
| \(2\) | \(1\) | \(0\) |
| \(4\) | \(9\) | \(1\) |
The graph of \(f\left(\dfrac{1}{2}x\right)\) is stretched horizontally by a factor of \(2 \) compared to the graph of \(f(x) \text{.}\) Further, if \((x,y) \) is a point on the graph of \(f(x)\text{,}\) then \((2x,y) \) is a point on the graph of \(f\left(\dfrac{1}{2}x\right)\text{.}\)
We can see this playing out in our example above. Notice that \((2,1) \) is a point on \(f(x)\text{,}\) and
\begin{equation*}
(2(2),1)=(4,1)
\end{equation*}
is a point on the graph of \(f\left(\dfrac{1}{2}x\right)\) as shown in the table and graph above. In general we have:
Horizontal Stretches, Compressions, and Reflections
Compared with the graph of \(y = f (x)\text{,}\) the graph of \(y = f (a\cdot x)\text{,}\) where \(a \ne 0\text{,}\) is
- compressed horizontally by a factor of \(\abs{a}\) if \(\abs{a}\gt 1\text{,}\)
- stretched horizontally by a factor of \(\abs{\dfrac{1}{a}}\) if \(0\lt\abs{a}\lt 1\text{,}\) and
- reflected about the \(y\)-axis (and stretched or compressed) if \(a\lt 0\text{.}\)
As you may have notice by now through our examples, a horizontal stretch or compression will never change the \(y\) intercepts. This is a good way to tell if such a transformation has occurred.
Example282
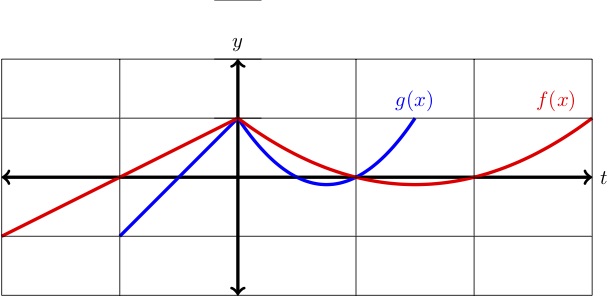
The graph of \(f(x)\) is shown along with either a horizontal stretch of compression of \(f(x) \text{.}\) Decide if \(g(x) \) is a stretch or a compression, and give a formula for \(g(x)\) in terms of \(f(x)\text{.}\)
Solution
First, notice that the \(y\)-intercept stays fixed while the \(x\)-intercepts shift closer to the \(y\)-axis. This tells us that \(g(x)\) is a horizontal compression. The \(x \)-intercepts of \(f(x)\) are \(x=-1,1,2 \) while the \(x\)-intercepts of \(g(x)\) are \(x=-.5,.5,1\text{.}\)
So, the \(x\)-intercepts of \(g(x) \) can be achieved by taking the intercepts of \(f(x) \) and divide each by 2. This tells us that \(g(x)\) is a horizontal compression by a factor of \(2 \text{.}\) Hence, we may write
\begin{equation*}
g(x)=f(2x).
\end{equation*}