MathematicsPreCalculus Mathematics at Nebraska

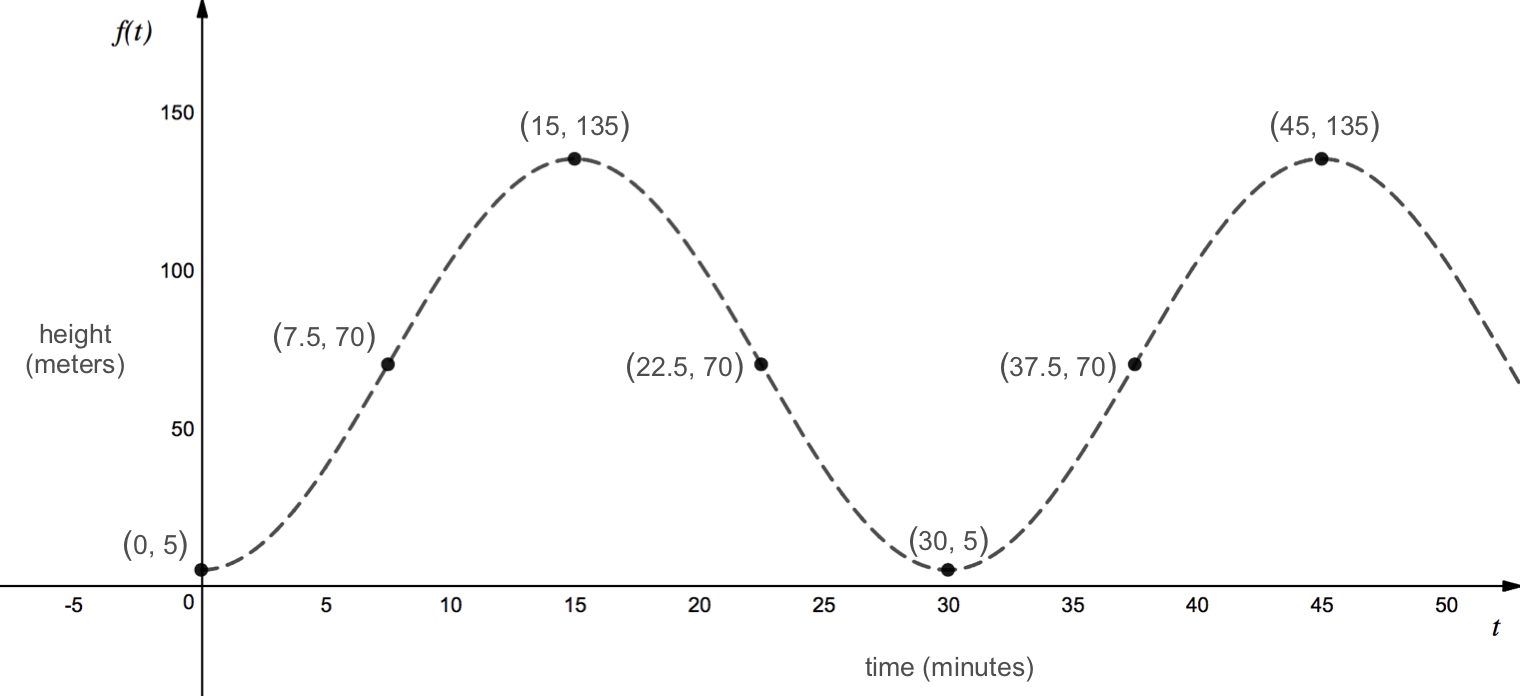
First, we need to determine what sinusoidal function to use. Since the graph of the function crosses the \(y\)-axis at its minimum value, then we should use a generalized cosine equation, so our function will be of the form \(f(t) = A\cos(B(t-h))+k \text{.}\) Since the function crosses \(y\)-axis at its minimum value, then \(A\) will be negative. Moreover, since there is no horizontal shift, then \(h = 0\text{.}\) To find \(A, B\text{,}\) and \(k\text{,}\) we need to find the amplitude, period, and midline.

As shown on the graph, the period of the function is 30 minutes. Therefore, the \(B\) value of the function is

Again, we assume that \(B\) is positive, so

The maximum value of the function is 135 meters and the minimum value is 5 meters. The midline is halfway in between these two values and can be found by averaging them:

Thus, the midline of the function is the line \(y=70\) meters, and

The amplitude of the function is the distance between the maximum value and the midline which is \(135-70=65\) meters. Therefore,

Putting this all together, the height of the individual \(t\) minutes after getting on the ride is given by

To check our solution, we can use a graphing calculator to graph the function we came up with and confirm that it matches the graph shown above.

We first need to decide what type of sinusoidal function to use. At \(t=0\) the wheel is in the 3 o'clock position; on the graph, this means that the point corresponding to \(t=0\) lies on the midline. This implies that we should use a sine function. So, our function is of the form \(f(t) = A\sin(B(t-h))+k \text{.}\) Since \(f(t)\) is at its midline at \(t=0\text{,}\) then there is no need for a horizontal shift of sine, so \(h=0\text{.}\) So, we are left to find \(A, B, \text{,}\) and \(k\text{.}\) To find these, we should find the amplitude, period, and midline of the function.

First, the wheel takes 3 minutes to complete a full rotation. This means that the height function repeats every 3 minutes, so the period is 3. The period \(P\) is related to \(B\text{,}\) the stretch/compression factor, by \(P=2\pi/B\text{:}\)

This means that \(B=\frac{2\pi}{3}\text{.}\) Let's assume that \(B\) is positive so that

The midline of the function is the horizontal line halfway between the function's maximum and minimum values. Since passengers board from a platform 10 feet above the ground, the minimum height is 10. The diameter of the wheel is 70 feet, so the top of the wheel is 80 feet off the ground (the 70 feet of the wheel plus the 10 feet off the ground). The number in the middle of 10 and 80 is 45, so the midline is at \(y=45\text{.}\) This means that \(k=45\text{.}\)

Finally, the amplitude is the distance between the function's maximum value and the midline. In this case, the distance between the maximum value of 80 and the midline of 45 is 35. Moreover, since at \(t=0\) a passenger is going up, then \(A\) should be positive, so \(A = 35\text{.}\)

Putting this all together, the height of the wheel at time \(t\) can be given by

Since the number of hours of daylight oscillates sinusoidally, we know we need to use either a generalized sine or generalized cosine function. The Summer Solstice is at \(t=0\text{,}\) and is at the maximum of the function since this is the highest number of daylight hours of the year. Since cosine is also at the maximum at \(t=0\text{,}\) this tells us we should use a generalized cosine function, so our function is of the form \(f(t) = A\cos(B(t-h))+k \text{.}\) Since \(f(t)\) is at its maximum at \(t=0\text{,}\) then there is no need for a horizontal shift of cosine, so \(h=0\text{.}\) So, we are left to find \(A, B, \text{,}\) and \(k\text{.}\) To find these, we should find the amplitude, period, and midline of the function.

Since the function repeats itself after one year and the unit for \(t\) is days, then the period of the function is \(365\text{.}\) We can use this to find \(B\text{,}\) since 365 = \frac{2\pi}{B}. Solving for \(B\text{,}\) we get \(B = \frac{2\pi}{365} \text{.}\)

The maximum of the function is 14.9 and the minimum is 9.43. To find the midline, we find the average of these two numbers:

So, our midline is \(y=12.165\text{,}\) and thus \(k = 12.165\text{.}\)

The amplitude is the distance between the midline and the maximum, which is \(14.9-12.165 = 2.735\text{.}\) Since \(f(t)\) is at its maximum at \(t=0\text{,}\) then we know that \(A\) is positive, so \(A = 2.735\text{.}\)

Putting this all together, the number of hours of daylight in Washington, D.C. \(t\) days after the Summer Solstice is