Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionReflections and Even and Odd Functions
In the previous section we discussed shifting a function horizontally and vertically. Now, we will take a look at what happens as we reflect a function across the \(x\)-axis or \(y\)-axis.
SubsectionReflection About y-axis
Let \(f(x)=(x+1)^2+1\text{,}\) and set
\begin{equation*}
h(x)=f(-x)=(-x+1)^2+1.
\end{equation*}
Compared to \(f(x)\text{,}\) the graph of \(h(x)\) is flipped, or reflected, about the \(y\)-axis as shown below.
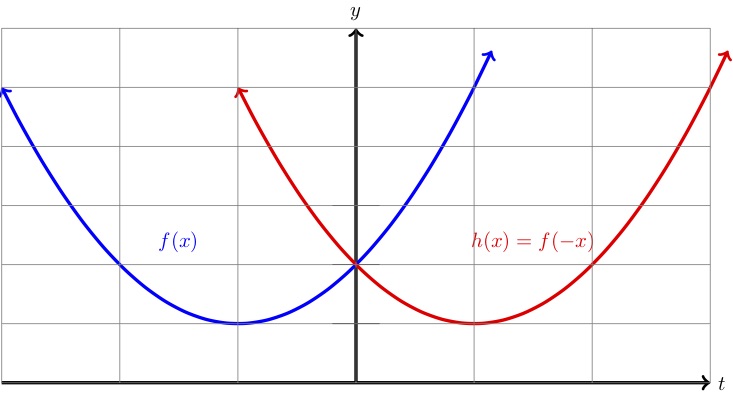
| \(x\) | \(f(x)\) | \(h(x)=f(-x)\) |
| \(-2\) | \(2\) | \(10\) |
| \(-1\) | \(1\) | \(5\) |
| \(0\) | \(2\) | \(2\) |
| \(1\) | \(5\) | \(1\) |
| \(2\) | \(10\) | \(2\) |
Looking at the graph and table above, we notice a relationship between the outputs of \(f(x) \) and \(f(-x)\) in this particular case, and as it so happens, this relationship holds in general.
Notice that if you take the column of output values for \(f(x)\) and flip them upside down you get the outputs of \(f(-x)\text{.}\) This makes sense as this is saying, for example,
\begin{equation*}
f(-2)=h(\alert{2})=f(-(\alert{2}))
\end{equation*}
as \(h(x)=f(-x)\text{.}\) In general, we have the following definition:
Reflection about y-axis
Compared with the graph of \(y=f(x)\text{,}\) the graph of \(f(-x)\) is reflected about the \(y\)-axis.
There are some functions which do not change when we apply a reflection about the \(y\)-axis. The most common example of this is the function \(y=x^2\text{.}\) Looking at a graph of this function, it is easy to see that when you reflect it across the \(y\)-axis it remains unchanged. These sorts of functions have a particular name:
Even Function
A function \(f\) is called an even function if
\begin{equation*}
f(x)=f(-x)
\end{equation*}
for all \(x \) in the domain of \(f \text{.}\) In other words, a function is even if performing a reflection about the \(y\)-axis does not change the graph of the function.
To help remember the definition of an even function, notice that the example of an even function we gave was of \(y=x^2\text{.}\) Other examples are \(y= x^4 \text{,}\) \(y=x^6 \text{,}\) \(y=x^8\text{,}\) etc. Notice that the exponent of each of these functions is an even number.
SubsectionReflection About x-axis
Compared to \(y=x^2\text{,}\) the graph of \(h(x) = -x^2\) is flipped, or reflected, about the \(x\)-axis. The \(y\)-coordinate of each point on the graph of \(y = x^2\) is replaced by its additive inverse.
| \(x\) | \(y=x^2\) | \(h(x)=-x^2\) |
| \(-2\) | \(4\) | \(-4\) |
| \(-1\) | \(1\) | \(-1\) |
| \(0\) | \(0\) | \(0\) |
| \(1\) | \(1\) | \(-1\) |
| \(2\) | \(4\) | \(-4\) |
In general, we have the following definition:
Reflection about x-axis
Compared with the graph of \(y=f(x)\text{,}\) the graph of \(-f(x)\) is reflected about the \(x\)-axis.
We now know that a function satisfying \(f(x)=f(-x)\) is an even function. While there do not exist any functions satisfying \(f(x)=-f(x)\text{,}\) we do have another type of symmetry to discuss here.
Example267
Consider the function \(f(x)=x^3 \text{.}\) If we reflect \(f \) about the \(y \)-axis, we get the function \(f(-x)\) as shown below:
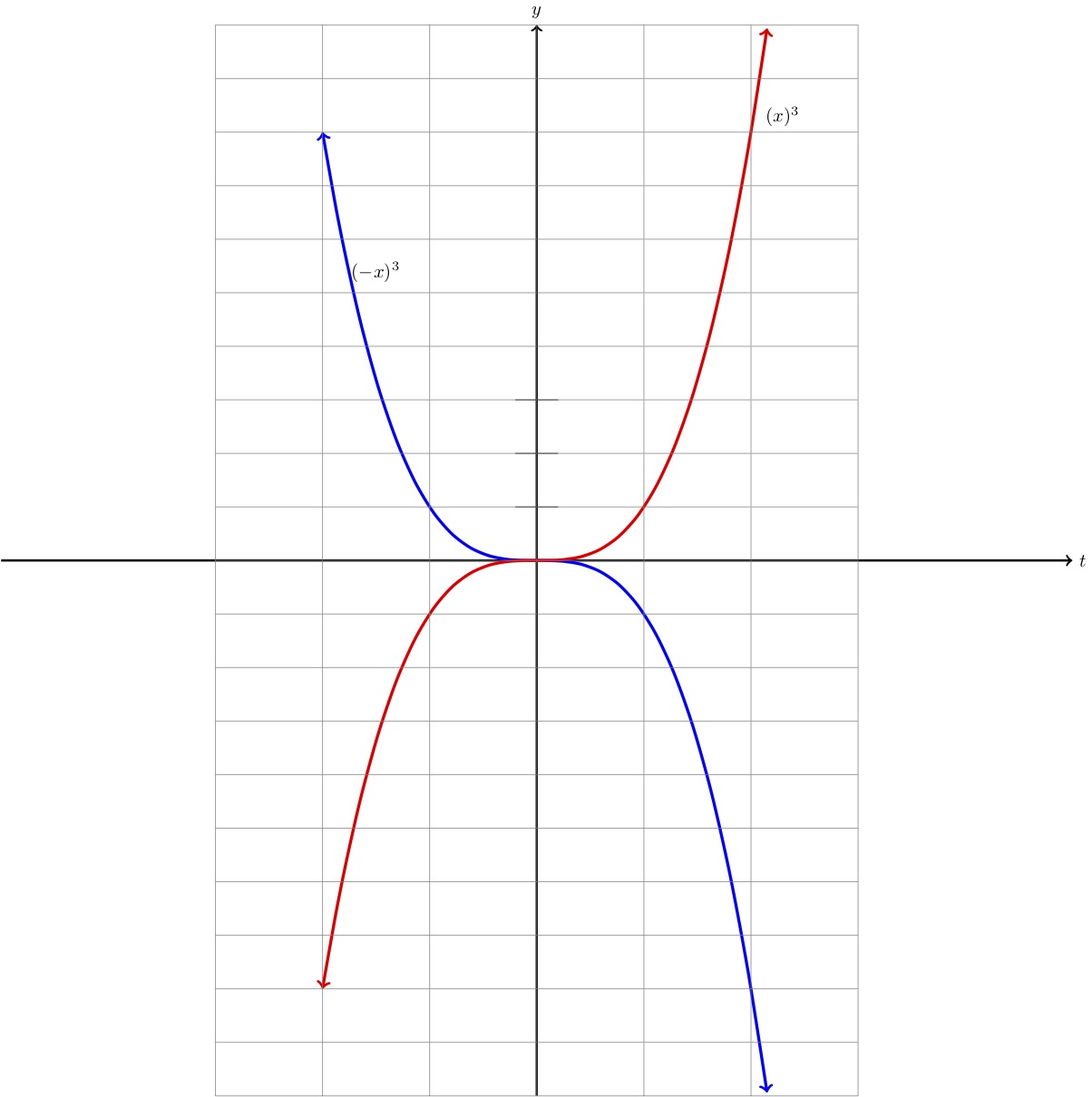
If we now reflect the function \(f(-x)\) about the \(x\) axis, we can see from the above picture that we end up back with the original function. As an equation, this says
\begin{equation*}
f(x)=-f(-x).
\end{equation*}
This type of function is said to have symmetry about the origin, or called an odd function.
Odd Function
A function \(f\) is called an odd function if
\begin{equation*}
f(x)=-f(-x)
\end{equation*}
for all \(x \) in the domain of \(f \text{.}\) In other words, a function is odd if performing a reflection about the \(y\)-axis and \(x\)-axis (doesn't matter which is performed first) does not change the graph of the function.
To help remember the definition of an odd function, we have a similar strategy as for even functions. Some examples of odd functions are \(y=x^3\text{,}\) \(y=x^5\text{,}\) \(y=x^7 \text{,}\) etc. Each of these examples have exponents which are odd numbers, and they are odd functions.