In this section, you will...
define and simplify algebraic fractions
identify the domain of algebraic fractions
add, subtract, multiply, and divide algebraic fractions
SectionAlgebraic Fractions
In the previous section, we saw a useful application of factoring polynomials, namely solving polynomial equations. In this section, we will explore another important application of factoring: algebraic fractions. Algebraic fractions are a special type of function, and factoring will allow us to simplify them as well as perform the four basic operations on them.
Supplemental Videos
The main topics of this section are also presented in the following videos:
SubsectionIdentifying Restrictions and Simplifying
Algebraic fractions, or rational functions, have the form
\begin{equation*}
r(x)=\frac{p(x)}{q(x)}\text{,}
\end{equation*}
where \(p(x)\) and \(q(x)\) are polynomials and \(q(x)\neq 0\text{.}\) The domain of an algebraic fraction will be identified with the domain or the rational function it defines and consists of all real numbers \(x\) except those where the denominator \(q(x)=0\text{.}\) Restrictions on the domain are real numbers for which the expression is undefined. For example, consider the function
\begin{equation*}
f(x)=\frac{(x-1)(x-3)}{(x-2)(x-3)}\text{.}
\end{equation*}
This is an algebraic fraction since (once expanded) both the numerator and denominator are polynomials. To find the domain, we need to consider what values of \(x\) will make the denominator equal to zero; in other words, the domain of this function is everything except the value(s) that solve \(0=(x-2)(x-3)\text{.}\) Applying the zero-factor property, we have
\begin{equation*}
\begin{aligned}
x-2\amp =0 \: \: \: \: \: \amp \text{ or }\: \: \: \: \: x-3\amp =0\\
x\amp =2\amp x\amp =3
\end{aligned}
\end{equation*}
Therefore, the original function is defined for any real number except \(2\) and \(3\text{.}\) We can express its domain using notation.
\begin{equation*}
x\neq 2,3 \: \: \: \: \: \text{ or }\: \: \: \: \: (-\infty, 2)\cup(2,3)\cup(3,\infty)
\end{equation*}
The restrictions to the domain of an algebraic fraction are determined by the denominator. Once the restrictions are determined we can cancel factors and obtain an equivalent function.
It is important to note that \(1\) is not a restriction to the domain because the expression is defined as \(0\) when the numerator is \(0\text{.}\) In fact, \(x=1\) is a root. This function is graphed below.
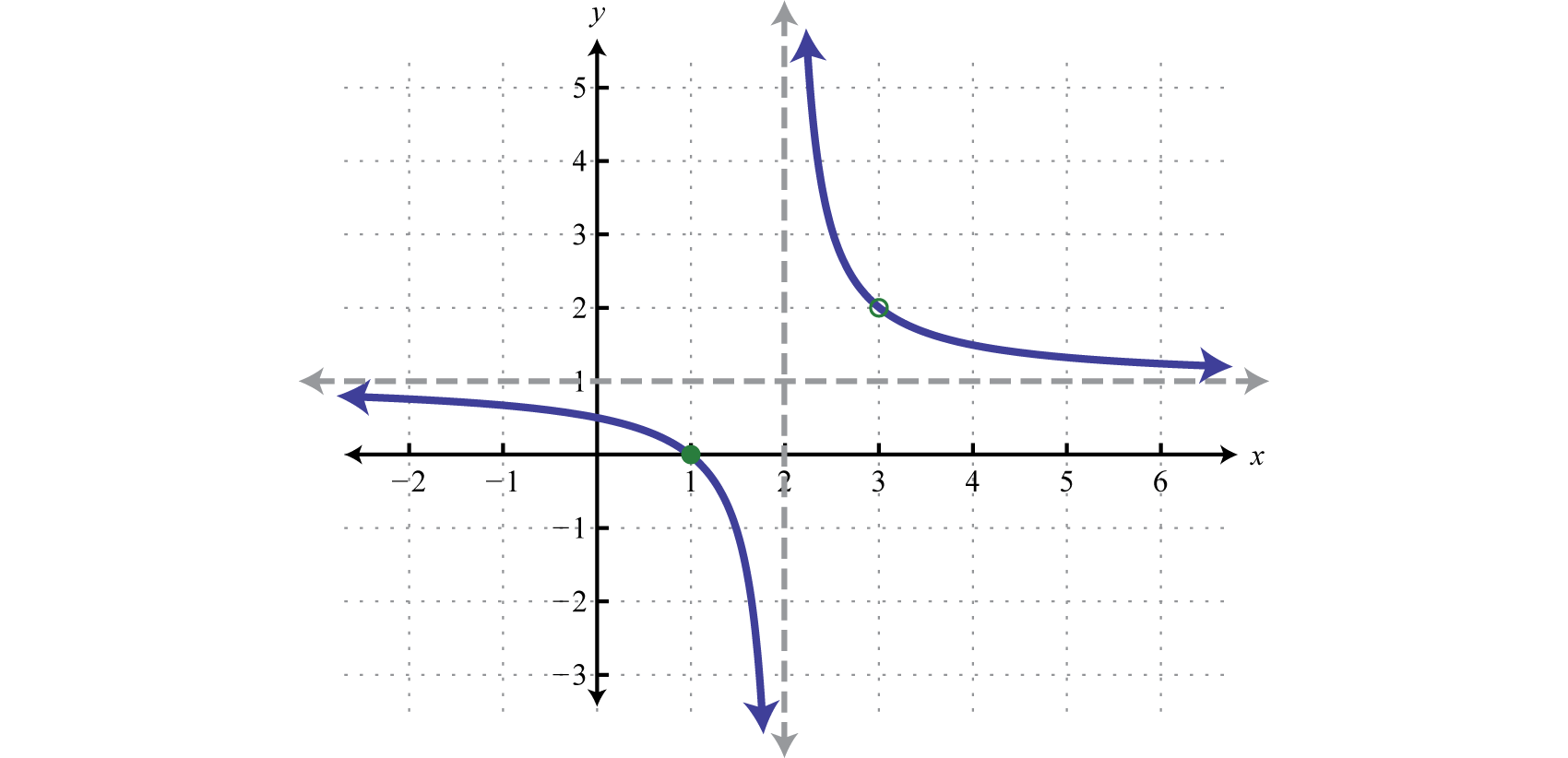
Notice that there is a vertical asymptote at the restriction \(x=2\) and the graph is left undefined at the restriction \(x=3\) as indicated by the open dot, or hole, in the graph. Graphing algebraic fractions in general is beyond the scope of this course. However, it is useful at this point to know that the restrictions are an important part of the graph of algebraic fractions.
Example176
State the restrictions and simplify the algebraic fraction \(g(x)=\frac{24x^7}{6x^5}\text{.}\)
Solution
Since \(g(x)\) is an algebraic fraction, it is undefined, or restricted, where its denominator is zero. Since the only solution of \(6x^5=0\) is \(x=0\text{,}\) the function is undefined where \(x\) is \(0\text{.}\)
\begin{equation*}
g(0)=\frac{24(0)^7}{6(0)^5}=\frac{0}{0} \: \: \: \alert{\text{Undefined}}
\end{equation*}
Therefore, the domain consists of all real numbers \(x\text{,}\) where \(x\neq 0\text{.}\) With this understanding, we can simplify by reducing the rational expression to lowest terms. Cancel common factors.
\begin{equation*}
g(x)=\frac{24x^7}{6x^5}=\frac{4x^7}{x^5}=4x^2
\end{equation*}
Our answer is \(g(x)=4x^2\text{,}\) where \(x\neq 0\text{.}\)
Example177
State the restrictions and simplify the algebraic fraction \(g(x)=\frac{2x^2+5x-3}{4x^2-1}\text{.}\)
Solution
Before we can identify the restrictions and simplify the function, we need to factor both the numerator and the denominator.
\begin{equation*}
\begin{aligned}
g(x)\amp =\frac{2x^2+5x-3}{4x^2-1}\\
\amp =\frac{(2x-1)(x+3)}{(2x+1)(2x-1)}
\end{aligned}
\end{equation*}
Since \(g(x)\) is an algebraic fraction, it is undefined, or restricted, where its denominator is zero. Applying the zero-factor principle, we have
\begin{equation*}
\begin{aligned}
2x+1\amp =0 \: \: \: \: \: \amp \text{ or }\: \: \: \: \: 2x-1\amp =0\\
2x\amp =-1\amp 2x\amp =1\\
x\amp =-\frac{1}{2}\amp x\amp =\frac{1}{2}
\end{aligned}
\end{equation*}
Therefore, the domain consists of all real numbers \(x\text{,}\) where \(x\neq -\frac{1}{2},\frac{1}{2}\text{.}\) With this understanding, we can simplify by reducing the rational expression to lowest terms. Cancel common factors.
\begin{equation*}
g(x)=\frac{(2x-1)(x+3)}{(2x+1)(2x-1)}=\frac{x+3}{2x+1}
\end{equation*}
Our answer is \(g(x)=\frac{x+3}{2x+1}\text{,}\) where \(x\neq -\frac{1}{2},\frac{1}{2}\text{.}\)
Occasionally we will have to factor out a negative one to simplify an algebraic fraction as much as possible.
Example178
State the restrictions and simplify the algebraic fraction \(g(x)=\frac{25-x^2}{x^2-10x+25}\text{.}\)
Solution
First, we factor the numerator and denominator.
\begin{equation*}
\begin{aligned}
g(x)\amp =\frac{25-x^2}{x^2-10x+25}\\
\amp =\frac{(5-x)(5+x)}{(x-5)(x-5)}\\
\amp = \frac{\alert{-1\cdot (x-5)}(5+x)}{(x-5)(x-5)}\\
\amp=\frac{-1(5+x)}{(x-5)}\\
\amp = -\frac{x+5}{x-5}\\
\end{aligned}
\end{equation*}
Our answer is \(g(x)=-\frac{x+5}{x-5}\text{,}\) where \(x\neq 5\text{.}\)
It is important to remember that we can only cancel factors of a product. A common mistake is to cancel terms.
Example179
State the restrictions and simplify \(f(x)=\frac{x-2x^2}{4x^4-x^2}\text{.}\)
Solution
Before we can identify the restrictions and simplify the function, we need to factor both the numerator and the denominator.
\begin{equation*}
\begin{aligned}
f(x)\amp= \frac{x-2x^2}{4x^4-x^2}\\
\amp= \frac{x(1-2x)}{x^2(2x+1)(2x-1)} \\
\amp= \frac{-x(2x-1)}{x^2(2x+1)(2x-1)}
\end{aligned}
\end{equation*}
Since \(f(x)\) is an algebraic fraction, it is undefined, or restricted, where its denominator is zero. Applying the zero-factor principle, we find that the restrictions are \(x=0,\frac{1}{2},-\frac{1}{2}\text{.}\)
Therefore, the domain consists of all real numbers \(x\text{,}\) where \(x\neq 0,\frac{1}{2},-\frac{1}{2}\text{.}\) With this understanding, we can simplify by reducing the rational expression to lowest terms. Cancel common factors.
\begin{equation*}
f(x)=\frac{-x(2x-1)}{x^2(2x+1)(2x-1)}=\frac{-1}{x(2x+1)}
\end{equation*}
Our answer is \(f(x)=-\frac{1}{x(2x+1)}\text{,}\) where \(x\neq 0,\frac{1}{2},-\frac{1}{2}\text{.}\)
In some examples, we will make a broad assumption that the denominator is nonzero. When we make that assumption, we do not need to determine the restrictions.
Example180
Given \(f(x)=x^2-2x+5\text{,}\) simplify \(\frac{f(x)-f(3)}{ax-3a}\text{.}\) Assume all denominators are nonzero.
Solution
First, we calculate \(f(3)\text{.}\)
\begin{equation*}
\begin{aligned}
f(3)\amp = (3)^2-2(3)+5\\
\amp = 9-6+5\\
\amp =3+5\\
\amp =8.
\end{aligned}
\end{equation*}
Now we substitute into the quotient.
\begin{equation*}
\begin{aligned}
\frac{f(x)-f(3)}{ax-3a}\amp = \frac{x^2-2x+5-8}{ax-3a}\\
\amp = \frac{x^2-2x-3}{ax-3a}\\
\amp =\frac{(x+1)(x-3)}{a(x-3)}\\
\amp =\frac{x+1}{a}
\end{aligned}
\end{equation*}
Our answer is \(\frac{f(x)-f(3)}{ax-3a}=\frac{x+1}{a}\text{.}\)
SubsectionMultiplying and Dividing Algebraic Fractions
Recall from Numbers and Operations that to multiply two fractions, we can multiply the numerators together, multiply the denominators together, and then reduce. Multiplying rational expressions is performed in a similar manner. In general, given polynomials \(P, Q, R,\) and \(S\text{,}\) where \(Q\neq 0\) and \(S\neq 0\text{,}\) we have
\begin{equation*}
\frac{P}{Q}\cdot\frac{R}{S}=\frac{PR}{QS}\text{.}
\end{equation*}
The restrictions to the domain of a product consist of the restrictions of each function.
Example181
Given \(f(x)=\frac{9x^2-25}{x-5}\) and \(g(x)=\frac{x^2-2x-15}{3x+5}\text{,}\) find \(f(x)\cdot g(x)\) and determine the restrictions on the domain.
Solution
In this case, the domain of \(f\) consists of all real numbers except \(5\text{,}\) and the domain of \(g\) consists of all real numbers except \(-\frac{5}{3}\text{.}\) Therefore, the domain of the product consists of all real numbers except \(5\) and \(-\frac{5}{3}\text{.}\) Multiply the functions and then simplify the result.
\begin{equation*}
\begin{aligned}
f(x)\cdot g(x) \amp =\frac{9x^2-25}{x-5}\cdot \frac{x^2-2x-15}{3x+5}\\
\amp =\frac{(3x+5)(3x-5)}{x-5}\cdot\frac{(x-5)(x+3)}{3x+5}\\
\amp =\frac{(3x+5)(3x-5)(x-5)(x+3)}{(x-5)(3x+5)}\\
\amp=\frac{(3x-5)(x+3)}{1}\\
\amp =(3x-5)(x+3)
\end{aligned}
\end{equation*}
Our answer is \(f(x)\cdot g(x)=(3x-5)(x+3)\) where \(x\neq 5,-\frac{5}{3}\text{.}\)
To divide two fractions, we multiply by the reciprocal of the divisor. Dividing rational expressions is performed in a similar manner. In general, given polynomials \(P, Q, R\text{,}\) and \(S\text{,}\) where \(Q\neq 0\text{,}\) \(R\neq 0\text{,}\) and \(S\neq 0\text{,}\) we have
\begin{equation*}
\frac{P}{Q}\div\frac{R}{S}=\frac{\frac{P}{Q}}{\frac{R}{S}}=\frac{P}{Q}\cdot \frac{S}{R}=\frac{PS}{QR}\text{.}
\end{equation*}
The restrictions to the domain of a quotient will consist of the restrictions of each function as well as the restrictions on the reciprocal of the divisor.
Example182
Given \(f(x)=\frac{2x^2+13x-7}{x^2-4x-21}\) and \(g(x)=\frac{2x^2+5x-3}{49-x^2}\text{,}\) find \(\frac{f(x)}{g(x)}\) and determine the restrictions on the domain.
Solution
We'll start by setting up the quotient and factoring each polynomial.
\begin{equation*}
\begin{aligned}
f(x)\div g(x) \amp =\frac{2x^2+13x-7}{x^2-4x-21} \div \frac{2x^2+5x-3}{49-x^2}\\
\amp= \frac{(2x-1)(x+7)}{(x+3)(x-7)} \div \frac{(2x-1)(x+3)}{(7+x)(7-x)}
\end{aligned}
\end{equation*}
To find the restrictions, we need to find the restrictions of \(f(x)\text{,}\) \(g(x)\text{,}\) as well as the reciprocal of \(g(x)\text{.}\) The restrictions of \(f(x)\) are \(-3\) and \(7\text{,}\) and the restrictions of \(g(x)\) are \(7\) and \(-7\text{,}\) and the reciprocal of \(g(x)\) has restrictions of \(-3\) and \(\frac{1}{2}\text{.}\) Therefore, the domain of this quotient consists of all real numbers except \(-3, \frac{1}{2}, 7\) and \(-7\text{.}\)
Next, to simplify the quotient, we perform the division and reduce.
\begin{equation*}
\begin{aligned}
f(x)\div g(x) \amp =\frac{2x^2+13x-7}{x^2-4x-21} \div \frac{2x^2+5x-3}{49-x^2}\\
\amp= \frac{(2x-1)(x+7)}{(x+3)(x-7)} \div \frac{(2x-1)(x+3)}{(7+x)(7-x)} \\
\amp= \frac{(2x-1)(x+7)}{(x+3)(x-7)} \cdot \frac{(7+x)(7-x)}{(2x-1)(x+3)} \\
\amp= \frac{(2x-1)(x+7)(7+x)(7-x)}{(x+3)(x-7)(2x-1)(x+3)} \\
\amp= \frac{(x+7)(7+x)(-1)}{(x+3)(x+3)}
\end{aligned}
\end{equation*}
Our answer is \(\left(\frac{f}{g}\right)(x)=-\frac{(x+7)^2}{(x+3)^2}\) where \(x\neq -3,\frac{1}{2},7,-7\text{.}\)
Exercise183
Given \(f(x)=\frac{2x+5}{3x^2+14x-5}\) and \(g(x)=\frac{6x^2+13x-5}{x+5}\text{,}\) find \(\left(\frac{f}{g}\right)(x)\) and determine the restrictions on the domain.
Solution
Our answer is \(\left(\frac{f}{g}\right)(x)=\frac{1}{(3x-1)^2}\) where \(x\neq -5,-\frac{5}{2},\frac{1}{3}\text{.}\)
SubsectionAdding and Subtracting Algebraic Fractions
Recall from Numbers and Operations that to multiply two fractions, we need a common denominator and then we can simply add or subtract the numerators and write the result over the common denominator. When working with rational expressions, the common denominator will be a polynomial. In general, given polynomials \(P, Q\text{,}\) and \(R\text{,}\) where \(Q\neq 0\text{,}\) we have the following:
\begin{equation*}
\frac{P}{Q}\pm\frac{R}{Q}=\frac{P\pm R}{Q}\text{.}
\end{equation*}
The set of restrictions to the domain of a sum or difference of rational expressions consists of the restrictions to the domains of each expression.
Example184
Perform the subtraction \(\frac{4x}{x^2-64}-\frac{3x+8}{x^2-64}\) and keep track of restrictions on the domain.
Solution
Since the denominators are the same, we can subtract the numerators and write the result over the common denominator. Take care to distribute the negative \(1\text{.}\)
\begin{equation*}
\begin{aligned}
\frac{4x}{x^2-64}-\frac{3x+8}{x^2-64}\amp = \frac{4x-(3x+8)}{x^2-64}\\
\amp = \frac{4x-3x-8}{x^2-64}\\
\amp = \frac{x-8}{(x+8)(x-8)}\\
\amp = \frac{1}{x+8}
\end{aligned}
\end{equation*}
Our solution is \(\frac{1}{x+8}\) for all real numbers \(x\neq \pm 8\text{.}\)
To add or subtract rational expressions with unlike denominators, we first find equivalent expressions with common denominators. We do this just as we have with fractions. If the denominators of fractions are relatively prime, then the least common denominator (LCD) is their product. For example,
\begin{equation*}
\frac{1}{x}+\frac{1}{y} \implies \text{LCD}=x\cdot y=xy.
\end{equation*}
Multiply each fraction by the appropriate form of \(1\) to obtain equivalent fractions with a common denominator.
\begin{equation*}
\begin{aligned}
\frac{1}{x}+\frac{1}{y}\amp =\frac{1}{x}\cdot\alert{\frac{y}{y}}+\frac{1}{y}\cdot\alert{\frac{x}{x}}\\
\amp = \frac{y}{xy}+\frac{x}{xy}\\
\amp = \frac{y+x}{xy}
\end{aligned}
\end{equation*}
In general, given polynomials \(P, Q, R\text{,}\) and \(S\text{,}\) where \(Q\neq 0\) and \(S\neq 0\text{,}\) we have the following:
\begin{equation*}
\frac{P}{Q}\pm\frac{R}{S}=\frac{PS\pm QR}{QS}
\end{equation*}
Example185
Given \(f(x)=\frac{5x}{3x+1}\) and \(g(x)=\frac{2}{x+1}\text{,}\) find \(f(x)+g(x)\) and determine the restrictions.
Solution
Here the LCD is the product of the denominators \((3x+1)(x+1)\text{.}\) We multiply by the appropriate factors to obtain rational expressions with a common denominator before adding.
\begin{equation*}
\begin{aligned}
(f+g)(x)\amp = f(x)+g(x)\\
\amp =\frac{5x}{3x+1}+\frac{2}{x+1}\\
\amp =\frac{5x}{3x+1}\cdot\alert{\frac{(x+1)}{(x+1)}}+\frac{2}{x+1}\cdot\alert{\frac{(3x+1)}{(3x+1)}}\\
\amp = \frac{5x(x+1)}{(3x+1)(x+1)}+\frac{2(3x+1)}{(x+1)(3x+1)}\\
\amp=\frac{5x(x+1)+2(3x+1)}{(3x+1)(x+1)}\\
\amp = \frac{5x^2+5x+6x+2}{(3x+1)(x+1)}\\
\amp =\frac{5x^2+11x+2}{(3x+1)(x+1)}\\
\amp =\frac{(5x+1)(x+2)}{(3x+1)(x+1)}\\
\end{aligned}
\end{equation*}
The domain of \(f\) consists all real numbers except \(-\frac{1}{3}\text{,}\) and the domain of \(g\) consists of all real numbers except \(-1\text{.}\) Therefore, the domain of \(f + g\) consists of all real numbers except \(-1\) and \(-\frac{1}{3}\text{.}\)
Our solution is \(\frac{(5x+1)(x+2)}{(3x+1)(x+1)}\) for all real numbers \(x\neq -1,-\frac{1}{3}\text{.}\)
It is not always the case that the LCD is the product of the given denominators. Typically, the denominators are not relatively prime; thus determining the LCD requires some thought. Begin by factoring all denominators. The LCD is the product of all factors with the highest power.
Example186
Given \(f(x)=\frac{3x}{3x-1}\) and \(g(x)=\frac{4-14x}{3x^2-4x+1}\text{,}\) find \(f-g\) and determine the restrictions.
Solution
To determine the LCD, factor the denominator of \(g\text{.}\)
\begin{equation*}
\begin{aligned}
(f-g)(x)\amp = f(x)-g(x)\\
\amp =\frac{3x}{3x-1} -\frac{4-14x}{3x^2-4x+1}\\
\amp=\frac{3x}{3x-1} -\frac{4-14x}{(3x-1)(x-1)}\\
\end{aligned}
\end{equation*}
In this case the LCD\(=(3x-1)(x-1)\text{.}\) Multiply \(f\) by \(1\) in the form of \(\frac{(x-1)}{(x-1)}\) to obtain equivalent algebraic fractions with a common denominator and then subtract.
\begin{equation*}
\begin{aligned}
(f-g)(x)\amp = f(x)-g(x)\\
\amp =\frac{3x}{3x-1}\cdot\alert{\frac{(x-1)}{(x-1)}} -\frac{4-14x}{(3x-1)(x-1)}\\
\amp=\frac{3x(x-1)-4+14x}{(3x-1)(x-1)}\\
\amp =\frac{(3x-1)(x+4)}{(3x-1)(x-1)}\\\\
\amp = \frac{(x+4)}{(x-1)}
\end{aligned}
\end{equation*}
The domain of \(f\) consists all real numbers except \(\frac{1}{3}\text{,}\) and the domain of \(g\) consists of all real numbers except \(1\) and \(\frac{1}{3}\text{.}\) Therefore, the domain of \(f - g\) consists of all real numbers except \(1\) and \(\frac{1}{3}\text{.}\)
Our solution is \(\frac{x+4}{x-1}\) for all real numbers \(x\neq 1, \frac{1}{3}\text{.}\)
Exercise187
Simplify \(\frac{-2x}{x+6}-\frac{3x}{6-x}-\frac{18(x-2)}{x^2-36}\) and determine the restrictions.
Solution
Our solution is \(\frac{x+6}{x-6}\) for all real numbers \(x\neq \pm 6\text{.}\)
Exercise188
Simplify \(\frac{x+1}{(x-1)^2}-\frac{2}{x^2-1}-\frac{4}{(x+1)(x-1)^2}\) and determine the restrictions.
Solution
Our solution is \(\frac{1}{x-1}\) for all real numbers \(x\neq \pm 1\text{.}\)