Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionFunction Composition
In Chapter 2 we gave a quick explanation of a composition of functions, in which we discovered the following:
Composing Functions
Given two functions \(f(x)\) and \(g(x)\text{,}\) the composition \(f(g(x))\) has the same input as \(g \text{,}\) but has the same output as \(f \text{.}\)
However, something we did not discuss in section 6.2 is when we can compose two given functions.
SubsectionWhen We Can Compose
Suppose that \(f(x) \) and \(g(x) \) are functions, and we wish to compose them as \(f(g(x))\text{.}\) In order for this composition to be possible, it must "make sense." In particular, we need the output of \(g(x)\) be contained in the input of \(f(x) \text{.}\) Let's see this through an example.
Example238
Suppose that \(f(x)\) is the function which has as its input the students in a given class, and the function outputs the student's favorite color. Suppose too that \(g(x)\) is the function which has as its input the buildings in Nebraska, and outputs the building's height in feet.
Does the composition \(f(g(x))\) make sense?
Solution
No. Recall that the notation \(f(g(x))\) indicates that we are evaluating the function \(f\) at an output value of \(g \text{.}\) Since the output of \(g \) is the height of a building and the possible input values for \(f \) are students in a given classroom, there is no way to evaluate \(f \) at an output value of \(g \text{.}\)
For example, if the composition were to make sense, then \(f(g(x))\) would be telling us the favorite color of a building of a given height. This is clearly nonsense.
SubsectionExamples of Compositions
As with most topics in mathematics, the best way to understand compositions of functions is by working with several examples. In your course packet you will get practice with several different ways to look at composition of functions, but let's work through a few together now.
Example239
Let \(f(x)=2x^2+e^x \) and \(g(x)=3x+1\text{.}\) Find the equation for the compositions \(f(g(x))\) and \(g(f(x))\text{.}\)
Solution
Let's start by finding the equation for \(g(f(x))\text{.}\) Start by rewriting the outer function, \(g(x) \text{,}\) with parenthesis around the input \(x \text{.}\) This will help us see where the input of the function \(g \) is located in the equation.
\begin{equation*}
g(x)=3(x)+1
\end{equation*}
Now, the composition \(g(f(x))\) is telling us that we are putting the output of \(f(x)\text{,}\) which is \(2x^2+e^x\text{,}\) in place of the input of \(g(x)\text{,}\) which is just \(x \text{.}\) We can accomplish this by putting \(2x^2+e^x\) in place of the \(x \) in the equation for \(g(x)\text{.}\) So, the equation for the composition is given by
\begin{equation*}
g(f(x))=3(2x^2+e^x)+1
\end{equation*}
Similarly, to find the equation of \(f(g(x))\text{,}\) we start by rewriting the function \(f(x) \) with parenthesis around the input \(x \text{.}\)
\begin{equation*}
f(x)=2(x)^2+e^{(x)}
\end{equation*}
Then, by the same reasoning as above, we simply need to put the out of \(g(x)\text{,}\) which is \(3x+1\text{,}\) in place of the input of \(f(x)\text{,}\) which is again just \(x \text{.}\) So, the other composition is given by
\begin{equation*}
f(g(x))=2(3x+1)^2+e^{(3x+1)}
\end{equation*}
In this next example we will focus less on being able to write an equation for the composition, but instead work on simply evaluating the composition at a few points.
Example240
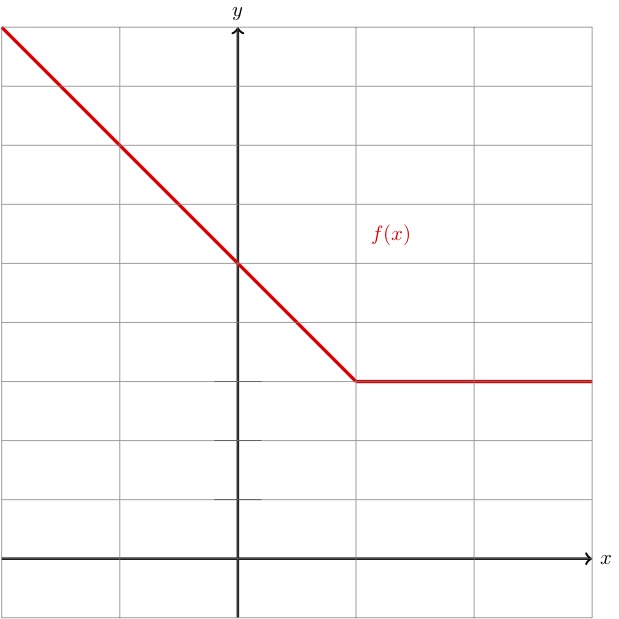
Below is the graph of the function \(f(x)\) and a table of values for the function \(g(x)\text{.}\) Using this information, identify the following values:
\(f(g(1)) \)
\(f(f(2))\)
\(g(g(3))\)
| \(x\) | \(g(x)\) |
| \(1\) | \(-2\) |
| \(2\) | \(0\) |
| \(3\) | \(2\) |
| \(4\) | \(10\) |
Solution
We will work through the solutions in the same order they were presented:
-
To find the value of \(f(g(1)) \text{,}\) we must first identify the interior value of \(g(1) \text{.}\) Looking at the table, we see
\begin{equation*} g(1)=-2 \end{equation*}So, replacing \(g(1)\) with \(-2 \) in the formula \(f(g(1))\) we have
\begin{equation*} f(g(1))=f(-2) \end{equation*}From the graph, we see that \(f(-2)=9\text{.}\) This tells us that
\begin{equation*} f(g(1))=f(-2)=9. \end{equation*} -
Using the same steps as outlined in the first problem, we first find the value \(f(2)\text{.}\) From the graph, we see
\begin{equation*} f(2)=3 \end{equation*}Since the graph also shows us that \(f(3)=3\text{,}\) we conclude that
\begin{equation*} f(f(2))=f(3)=3. \end{equation*} -
From the table, we have \(g(3)=2\text{,}\) and \(g(2)=0\text{.}\) So, it must be that
\begin{equation*} g(g(3))=g(2)=0. \end{equation*}