Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionComplex Numbers
All the mathematical work you have done so far has involved using real numbers. In this section, we will work with a new set of numbers called the complex numbers. It should be noted that the real numbers are actually a special case of the complex numbers. This will be explained in more detail later in this section.
SubsectionMotivation
Let's start by providing some background as to where complex numbers arise from. Suppose that we want to solve for the \(x\)-intercepts of \(f(x) = x^2 -2x + 2\text{.}\) We can use the quadratic formula to obtain the \(x\)-intercepts, and when doing so, we obtain the following expression:
\begin{equation*}
x = \frac{-(-2) \pm \sqrt{(-2)^2-4(1)(2)}}{2(1)} = \frac{2 \pm \sqrt{-4}}{2}\text{.}
\end{equation*}
Notice that \(\sqrt{-4}\) is not a real number because there are no real numbers whose square is negative. As a result, \(f(x) = x^2 -2x + 2\) has no real \(x\)-intercepts. We can also verify this graphically since the graph of \(f(x) = x^2 - 2x + 2\) never crosses the \(x\)-axis.
SubsectionImaginary Numbers
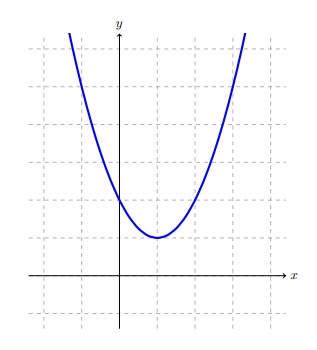
Even though the square root of a negative number is not a real number, there are many instances when we would like to be able to use it (e.g., finding the solutions to \(x^2-2x+2 = 0\)). So, we need to define a new set of numbers that are not real numbers.
Imaginary Numbers
An imaginary number is of the form
\begin{equation*}
\sqrt{-a} = \sqrt{a}\sqrt{-1} = \sqrt{a}i
\end{equation*}
where \(a > 0\) is a real number and \(i\) is an imaginary unit. Here, \(i\) is defined as \(i = \sqrt{-1}\) or \(i^2 = -1\text{.}\)
Note122
Unless stated otherwise, the letter \(i\) is used to represent a constant, not a variable!
Let's refer back to the motivational example introduced earlier in this section. The value \(\sqrt{-4}\) can be expressed as follows:
\begin{align*}
\sqrt{-4} \amp= \sqrt{4(-1)}\\
\amp= \sqrt{4}\sqrt{-1} \\
\amp= \sqrt{4}i \\
\amp= 2i
\end{align*}
Here are more examples of imaginary numbers \(5i\text{,}\) \(\frac{2}{3}i\text{,}\) \(-24i\text{,}\) and \(\sqrt{15}i\text{.}\)SubsectionComplex Numbers
Recall that when solving for the \(x\)-intercepts of \(f(x) = x^2 -2x + 2\text{,}\) we obtained the following values for \(x\) with the quadratic formula:
\begin{equation*}
x = \frac{2\pm \sqrt{-4}}{2}\text{.}
\end{equation*}
Using our new established knowledge of imaginary numbers, we find that
\begin{equation*}
x = \frac{2\pm 2i}{2}
\end{equation*}
which implies that \(x = 1 + i\) or \(x = 1 - i\text{.}\) These \(x\)-values are examples of complex numbers.
Complex Numbers
A complex number is of the form
\begin{equation*}
z = a + bi
\end{equation*}
where \(a\) and \(b\) are real numbers. Here, \(a\) is called the real part and \(b\) is called the imaginary part.
Note123
From this definition, we can observe that all real numbers are actually complex numbers with imaginary part equal to \(0\text{.}\) Moreover, imaginary numbers are actually complex numbers with real part equal to \(0\text{;}\) these numbers are called pure imaginary numbers
The real and imaginary parts of a complex number can never be combined. Here is a result that tells us when two complex numbers are equal.
Equality of Complex Numbers
Two complex numbers \(z = a+bi\) and \(w = c+di\) are equal if and only if \(a = c\) and \(b = d\text{.}\)
SubsectionArithmetic of Complex Numbers
Like real numbers, we can add, subtract, multiply, and divide complex numbers.
Sum and Difference of Complex Numbers
Consider two complex number \(z = a+bi\) and \(w = c+di\text{.}\) Then their sum is given by
\begin{equation*}
z+w = (a+bi) + (c+di) = (a+c) + (b+d)i\text{,}
\end{equation*}
and their difference is given by
\begin{equation*}
z-w = (a+bi) - (c+di) = (a-c) + (b-d)i\text{.}
\end{equation*}
Example124
Compute \((4+5i) + (8-6i)\) and \((2-3i) - (5+2i)\text{.}\)
Solution
\begin{align*}
(4+5i) + (8-6i) \amp= (4+8) + (5-6)i\\
\amp= 12 + (-1)i\\
\amp= 12 - i
\end{align*}
and
\begin{align*}
(2-3i) - (5+2i) \amp= (2-5) - (-3+2)i\\
\amp= (-3) - (-1)i \\
\amp= -3 + i
\end{align*}
When taking the product of two complex numbers, you should always remember that
\begin{equation*}
i^2 = -1\text{.}
\end{equation*}
Finding the product of two pure imaginary numbers is relatively straightforward.
Product of Pure Imaginary Numbers
Consider two pure imaginary numbers \(z = ai\) and \(w = bi\text{.}\) Then their product is given by
\begin{equation*}
zw = (ai)(bi) = (ab)i^2 = -ab\text{.}
\end{equation*}
Finding the product of two complex numbers is slightly different since we need to use the distributive property.
Product of Complex Numbers
Consider two complex numbers \(z = a+bi\) and \(w = c+di\text{.}\) Then their product is given by
\begin{equation*}
zw = (a+bi)(c+di) = (ac - bd) + (ad + bc)i\text{.}
\end{equation*}
Example125
Compute \((3i)(4i)\) and \((2+3i)(-3-2i)\text{.}\)
Solution
\begin{align*}
(3i)(4i) \amp= (3\cdot 4)i^2 \\
\amp= 12(-1)\\
\amp= -12
\end{align*}
and
\begin{align*}
(2+3i)(-3-2i) \amp= (2(-3) - 3(-2)) + (2(-2) + 3(-3))i\\
\amp= (-6 + 6) + (-4-9)i\\
\amp= 0 - 13i\\
\amp= -13i
\end{align*}
WARNING: The following property is true with real numbers, but it is not true with complex numbers:
\begin{equation*}
\sqrt{ab} = \sqrt{a}\sqrt{b}\text{.}
\end{equation*}
Here is a counter-example: let \(a = b = -2\text{.}\) Then,
\begin{equation*}
\sqrt{ab} = \sqrt{(-2)(-2)} = \sqrt{4} = 2\text{,}
\end{equation*}
but
\begin{align*}
\sqrt{a}\sqrt{b} \amp= \sqrt{-2}\sqrt{-2}\\
\amp= (\sqrt{2}i)(\sqrt{2}i)\\
\amp= (\sqrt{2})^2i^2\\
\amp = 2(-1) = -2.
\end{align*}
Hence,
\begin{equation*}
\sqrt{ab} \neq \sqrt{a}\sqrt{b}
\end{equation*}
(especially when \(a\text{,}\) \(b\) are both negative).
Finding the quotient of two complex numbers requires us to use the technique of rationalizing the denominator. We will consider two different types of quotients: division by a pure imaginary number and division by a complex number.
Division by a Pure Imaginary Number
Consider a complex number \(z = a+bi\) and a pure imaginary number \(w = ci\text{.}\) Then,
\begin{equation*}
\frac{z}{w} = \frac{a+bi}{ci} = \frac{a+bi}{ci}\cdot \frac{i}{i} = \frac{(a+bi)i}{ci^2} = \frac{-b + ai}{-c} = \frac{b - ai}{c}\text{.}
\end{equation*}
When dividing by a complex number, we rationalize the denominator by multiplying the complex conjugate.
Complex Conjugate
For any complex number \(z = a + bi\text{,}\) the number
\begin{equation*}
\bar{z} = a - bi
\end{equation*}
is called the complex conjugate of \(z\text{.}\)
The product of a complex number and its conjugate is a real number. That is,
\begin{equation*}
z\bar{z} = (a+bi)(a-bi) = a^2 -abi + abi - b^2i^2 = a^2 - b^2(-1) = a^2 + b^2\text{.}
\end{equation*}
Quotient of Two Complex Numbers
Consider two complex numbers \(z = a+bi\) and \(w = c + di\text{.}\) Then,
\begin{equation*}
\frac{z}{w} = \frac{a+bi}{c+di} = \frac{a+bi}{c+di} \cdot \frac{c-di}{c-di}
\end{equation*}
\begin{equation*}
= \frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}i\text{.}
\end{equation*}
Example126
Compute \(\frac{8+9i}{2i}\) and \(\frac{4-2i}{2+3i}\text{.}\)
Solution
\begin{align*}
\frac{8+9i}{2i} \amp= \frac{8+9i}{2i}\cdot\frac{i}{i}\\
\amp= \frac{(8+9i)i}{2i^2}\\
\amp= \frac{8i + 9i^2}{2(-1)}\\
\amp= \frac{8i + 9(-1)}{-2}\\
\amp= \frac{-9+8i}{-2}\\
\amp= \frac{9-8i}{2}
\end{align*}
and
\begin{align*}
\frac{4-2i}{2+3i} \amp= \frac{4-2i}{2+3i}\cdot \frac{2-3i}{2-3i}\\
\amp= \frac{(4-2i)(2+3i)}{(2)^2 + (3)^2}\\
\amp= \frac{(4(2)-(-2)(3)) + (4(3)+(-2)(2))i}{13}\\
\amp= \frac{(8+6)+(12-4)i}{13}\\
\amp= \frac{14+8i}{13}\\
\amp= \frac{14}{13}+\frac{8}{13}i
\end{align*}
SubsectionGraphing Complex Numbers
Like real numbers, we can also graph complex numbers. In order to plot a complex number, we will utilize a plane called the complex plane. The complex plane has two axes: a horizontal axis (which we will call the real axis) to plot the real part, and a vertical axis (which we will call the imaginary axis) to plot the imaginary part. In addition, the point where the real and imaginary axes cross is called the origin, and it is denoted by \((0,0)\text{.}\)
Plotting a Complex Number
To plot a complex number \(z = a + bi\text{,}\) we move \(a\) units in the horizontal direction and then we move \(b\) units in the vertical direction. Here, \(\text{Re}(z) = a\) and \(\text{Im}(z) = b\text{.}\)
Example127
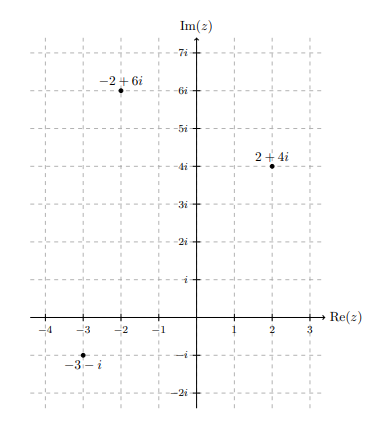
Plot the complex numbers \(2+4i\text{,}\) \(-2+6i\text{,}\) and \(-3-i\) in the complex plane
SolutionTo plot \(2+4i\text{,}\) we move \(2\) units to the right from the origin, and then we move \(4\) units up. To plot \(-2+6i\text{,}\) we move \(2\) units to the left from the origin, and then we move \(6\) units up. To plot \(-3-i\text{,}\) we move \(3\) units to the left from the origin, and then we move \(1\) unit down.
Note128
Whenever we plot a complex number \(z = a + bi\text{,}\) we sometimes use the notation \((a,b)\) to denote a point in the complex plane. In this context, \((a,b)\) represents a single complex number whose real part is \(a\) and imaginary part is \(b\text{.}\)
Modulus of a Complex Number
The modulus of a complex number \(z = a + bi\) is given by
\begin{equation*}
|z| = \sqrt{a^2+b^2}
\end{equation*}
Observe that \(|z| \geq 0\text{.}\)
Example129
Compute the modulus of \(z = 3 + 4i\) and \(w = -1 + i\text{.}\)
SolutionIf \(z = 3+4i\text{,}\) then \(a=3\) and \(b=4\text{.}\) Hence,
\begin{equation*}
|z| = \sqrt{3^2 + 4^2} = \sqrt{25} = 5
\end{equation*}
Similarly, if \(w=-1+i\text{,}\) then \(a=-1\) and \(b = 1\text{.}\) Hence,
\begin{equation*}
|w| = \sqrt{(-1)^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2}
\end{equation*}
Example130
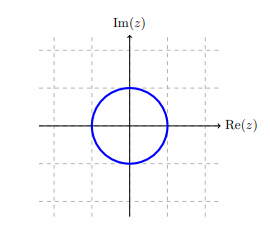
Plot all points in the complex plane that satisfy the equation \(|z| = 1\text{.}\)
SolutionThe points in the complex plane that satisfy the equation \(|z| = 1\) all have a distance of \(1\) unit from the origin. This means that all these points lie on a circle of radius \(1\) centered at the origin.
SubsectionComplex Numbers and Trigonometry
Now that we have familiarized ourselves with complex numbers, we are ready to make some connections to trigonometry. In the previous subsection, we talked about how to plot a complex number \(z = a+bi\) as a point \((a,b)\) in the complex plane. Moreover, we talked about how the point \((a,b)\) has a distance of \(|z|=\sqrt{a^2+b^2}\) from the origin. We can use our knowledge of polar coordinates to express a complex number in terms of the trigonometric functions \(\sin(\theta)\) and \(\cos(\theta)\text{.}\) Recall that when converting a Cartesian coordinate \((x,y)\) to a polar coordinate \((r,\theta)\text{,}\) we used the following formulas:
\begin{equation*}
r^2 = x^2+y^2
\end{equation*}
\begin{equation*}
\cos(\theta) = \frac{x}{r}
\end{equation*}
\begin{equation*}
\sin(\theta) = \frac{y}{r}
\end{equation*}
\begin{equation*}
\tan(\theta) = \frac{y}{x}, \ x \neq 0
\end{equation*}
The process of finding the polar form of a complex number is analogous. Let's consider a motivational example. Suppose that we have the complex number \(z = 1 + i\text{.}\) We can plot \(z\) as follows in the complex plane.
\begin{equation*}
|z| = \sqrt{2}
\end{equation*}
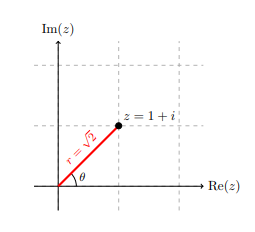
For convenience, put \(r = |z|\text{.}\) Observe that the ray drawn from the origin to the point \((1,1)\) makes an angle \(\theta\) from the real axis. Then, we can use right triangle trigonometry to write \(a\) and \(b\) as follows:
\begin{equation*}
a = r\cos(\theta) = \sqrt{2}\cos(\theta)=1
\end{equation*}
\begin{equation*}
b = r\sin(\theta) = \sqrt{2}\sin(\theta)=1
\end{equation*}
and
\begin{equation*}
\tan(\theta) = \frac{b}{a} = 1
\end{equation*}
Since \(\tan(\theta) = 1\) and \(a\text{,}\) \(b > 0\text{,}\) the unit circle tells us that \(\theta = \frac{\pi}{4}\text{.}\) This means that
\begin{equation*}
a = \sqrt{2}\cos(\frac{\pi}{4})
\end{equation*}
and
\begin{equation*}
b = \sqrt{2}\sin(\frac{\pi}{4})
\end{equation*}
Putting things together, the polar form of \(z = 1 + i\) is given by
\begin{equation*}
z = \sqrt{2}\cos(\frac{\pi}{4}) + \sqrt{2}\sin(\frac{\pi}{4})i = \sqrt{2}\big(\cos(\frac{\pi}{4}) + i\sin(\frac{\pi}{4}))
\end{equation*}
Polar Form for a Complex Number
The complex number \(z = a+bi\) in polar form is given by
\begin{equation*}
z = r(\cos(\theta) + i\sin(\theta))
\end{equation*}
Here, \(r = \sqrt{a^2+b^2}\text{,}\) \(a = r\cos(\theta)\text{,}\) \(b = r\sin(\theta)\text{,}\) and \(\tan(\theta) = \frac{b}{a}\) (assuming that \(a \neq 0\)). Moreover, \(0 \leq \theta \le 2\pi\) is called the argument of the complex number and \(r\) is its modulus.
SubsectionProducts and Quotients in Polar Form
A key reason for working with complex numbers in polar form is that it makes computing the product and quotient of complex numbers more manageable.
Product in Polar Form
If \(z = r(\cos(\alpha)+i\sin(\alpha))\) and \(w = R(\cos(\beta)+i\sin(\beta))\text{,}\) then
\begin{equation*}
zw = rR(\cos(\alpha+\beta) + i\sin(\alpha+\beta))
\end{equation*}
Observe that the formula for computing the product of two complex numbers in polar form requires us to simply multiply their moduli and add their arguments. Here's a quick verification of how to obtain the formula for the product using the sum identities for sine and cosine:
\begin{align*}
zw \amp= r(\cos(\alpha)+i\sin(\alpha))\cdot R(\cos(\beta)+i\sin(\beta))\\
\amp= rR(\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)) + i(\sin(\beta)\cos(\alpha)+\sin(\alpha)\cos(\beta))\\
\amp = rR(\cos(\alpha+\beta)+i\sin(\alpha+\beta))
\end{align*}
Example131
Use polar form to compute the product of \(z=1+i\) and \(w =-1-i\text{.}\)
SolutionYou should verify that \(z = \sqrt{2}(\cos(\frac{\pi}{4}) + i\sin(\frac{\pi}{4}))\) and \(w = \sqrt{2}(\cos(\frac{5\pi}{4})+i\sin(\frac{5\pi}{4}))\text{.}\) Then,
\begin{align*}
zw \amp= (\sqrt{2})(\sqrt{2})(\cos(\frac{\pi}{4}+\frac{5\pi}{4})+i\sin(\frac{\pi}{4}+\frac{5\pi}{4}))\\
\amp= 2(\cos(\frac{6\pi}{4})+i\sin(\frac{6\pi}{4}))\\
\amp= 2(\cos(\frac{3\pi}{2})+i\sin(\frac{3\pi}{2}))\\
\amp= 2(0+i(-1))\\
\amp= -2i
\end{align*}
Quotient in Polar Form
If \(z = r(\cos(\alpha)+i\sin(\alpha))\) and \(w = R(\cos(\beta)+i\sin(\beta))\text{,}\) then
\begin{equation*}
\frac{z}{w}= \frac{r}{R}(\cos(\alpha-\beta) + i\sin(\alpha-\beta))
\end{equation*}
Example132
Use polar form to compute the quotient of \(z=1+i\) and \(w =-1-i\text{.}\)
SolutionYou should verify that \(z = \sqrt{2}(\cos(\frac{\pi}{4}) + i\sin(\frac{\pi}{4}))\) and \(w = \sqrt{2}(\cos(\frac{5\pi}{4})+i\sin(\frac{5\pi}{4}))\text{.}\) Then,
\begin{align*}
\frac{z}{w} \amp= \frac{\sqrt{2}}{\sqrt{2}}(\cos(\frac{\pi}{4}-\frac{5\pi}{4})+i\sin(\frac{\pi}{4}-\frac{5\pi}{4}))\\
\amp= (\cos(-\frac{4\pi}{4})+i\sin(-\frac{4\pi}{4}))\\
\amp= (\cos(-\pi)+i\sin(-\pi)\\
\amp= (-1+i(0))\\
\amp= -1
\end{align*}
SubsectionPowers and Roots of Complex Numbers
We can also use polar form to compute the powers and roots of a complex number with feasibility. For example, if \(z = r(\cos(\theta)+i\sin(\theta))\text{,}\) then using the double-angle formulas we find that
\begin{align*}
z^2 \amp= (r(\cos(\theta)+i\sin(\theta))^2\\
\amp= r^2\big((\cos^2(\theta)-\sin^2(\theta))+i(2\sin(\theta)\cos(\theta))\big) \\
\amp= r^2\big(\cos(2\theta)+i\sin(2\theta)\big)
\end{align*}
Hence,
\begin{equation*}
z^2 = r^2\big(\cos(2\theta)+i\sin(2\theta)\big)
\end{equation*}
In general, for any positive integer \(n\text{,}\) a complex number raised to the \(n\)-th power is given by the following theorem.
De Moivre's Theorem
If \(z = r(\cos(\theta)+i\sin(\theta))\) is a complex number in polar form and \(n\) is a positive integer, then
\begin{equation*}
z^n = r^n\big(\cos(n\theta)+i\sin(n\theta)\big)
\end{equation*}
Example133
Let \(z = \sqrt{3}+i\text{.}\) Compute \(z^4\text{.}\)
SolutionYou should verify that \(z = 2\big(\cos(\frac{\pi}{6}) + i\sin(\frac{\pi}{6})\big)\text{.}\) Using De Moivre's Theorem, we find that
\begin{align*}
z^4 \amp= 2^4\big(\cos(4\cdot\frac{\pi}{6}) + i\sin(4\cdot \frac{\pi}{6})\big)\\
\amp= 16\big(\cos(\frac{2\pi}{3})+i\sin(\frac{2\pi}{3})\big)\\
\amp= 16\big(-\frac{1}{2} + i\cdot\frac{\sqrt{3}}{2}\big)\\
\amp= -8 + 8\sqrt{3}i
\end{align*}
\begin{equation*}
z^\frac{1}{2} = r^\frac{1}{2}\big(\cos(\frac{1}{2}\theta)+i\sin(\frac{1}{2}\theta)\big)
\end{equation*}
Recall that every number (whether it's real or complex) has two square roots. In the case of complex numbers, we find the other root by adding a multiple of \(2\pi\) to the argument of \(z\text{.}\) So, the polar form of \(z\) can also be given by
\begin{equation*}
z = r\big(\cos(\theta + 2\pi)+i\sin(\theta+2\pi)\big)
\end{equation*}
Using De Moivre's Theorem, the second square root of \(z\) is then given by
\begin{equation*}
r^\frac{1}{2}\big(\cos(\frac{\theta}{2}+\pi) + i\sin(\frac{\theta}{2}+\pi)\big)
\end{equation*}
Roots of a Complex Number
A complex number \(z = r(\cos(\theta)+i\sin(\theta))\) in polar form has \(n\) complex \(n\)-th roots given by
\begin{equation*}
z_k = r^\frac{1}{n}\bigg(\cos\big(\frac{\theta+2\pi k}{n}\big)+i\sin\big(\frac{\theta+2\pi k}{n}\big)\bigg)
\end{equation*}
where \(k = 0\text{,}\) \(1\text{,}\) \(2\text{,}\) ..., \(n-1\text{.}\)
Example134
Find the square roots of \(z = i\text{.}\)
SolutionYou should verify that \(z = \sin(\frac{\pi}{2})i\text{,}\) \(\theta = \frac{\pi}{2}\text{,}\) \(r = 1\text{.}\) and \(n = 2\text{.}\) Then,
\begin{align*}
z_0 \amp= (1)^\frac{1}{2}\bigg(\cos\big(\frac{\frac{\pi}{2}+2\pi(0)}{2}\big) + i\sin\big(\frac{\frac{\pi}{2}+2\pi(0)}{2}\big)\bigg)\\
\amp= \cos(\frac{\pi}{4})+i\sin(\frac{\pi}{4})\\
\amp= \frac{1}{\sqrt{2}} + i\cdot\frac{1}{\sqrt{2}}\\
\amp= \frac{1}{\sqrt{2}}(1+i)
\end{align*}
and
\begin{align*}
z_1 \amp= (1)^\frac{1}{2}\bigg(\cos\big(\frac{\frac{\pi}{2}+2\pi(1)}{2}\big) + i\sin\big(\frac{\frac{\pi}{2}+2\pi(1)}{2}\big)\bigg)\\
\amp= \cos(\frac{5\pi}{4})+i\sin(\frac{5\pi}{4})\\
\amp= -\frac{1}{\sqrt{2}} + i\cdot\bigg(- \frac{1}{\sqrt{2}} \bigg)\\
\amp= -\frac{1}{\sqrt{2}}(1+i)
\end{align*}
Hence, the square roots of \(z=i\) are given by \(\pm \frac{1}{\sqrt{2}}(1+i)\text{.}\)