In this section, you will...
translate verbal descriptions into equations
write and solve linear equations to represent real world applications
SectionApplications of Linear Equations
Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. In this section, we will solve several types of real world problems using algebra.
Supplemental Videos
The main topics of this section are also presented in the following videos:
To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.
| Key Words | Translation |
| Sum: increased by, more than, plus, added to, total | \(+\) |
| Difference: decreased by, subtracted from, less, minus | \(-\) |
| Product: multiplied by, of, times, twice | \(\cdot\) |
| Quotient: divided by, ratio, per | \(\div\) |
| Equals: is, total, result | \(=\) |
When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify what needs to be represented by a variable, and then specify what that variable will be. For instance, if we are solving a word problem that asks us to find the distance that a car travelled, we likely will want to define a variable to represent the distance the car travelled. It is important to be specific and include units if applicable: it is better to say "\(d=\)the distance travelled by the car in miles" than simply saying "\(d=\)distance".
In the previous paragraph, we chose the variable \(d\) to represent distance. You can choose any letter for your variables, but it can be helpful to chose a letter that aligns with what the variable represents (such as \(d\) for distance, \(t\) for time, etc.). However, we often just use \(x\text{.}\) As long as you clearly define your variables, it does not matter what variables you use.
Before we work with word problems, we will first practice translating simple sentences into equations.
Example65
Write an equation for the sequence of operations to describe each situation below.
\(x\) is \(9\) more than \(y\text{.}\)
Half of \(x\) is \(y\text{.}\)
\(x\) is \(30\%\) of \(y\text{.}\)
Solution
In all of these examples, it can be helpful to think of the word "is" as the equals sign.
\(x\) is \(9\) more than \(y\) means that \(x=y+9\text{.}\)
Half of \(x\) is \(y\) means that \(\frac{1}{2}x=y\text{.}\)
\(x\) is \(30\%\) of \(y\) means that \(x=0.30y\text{.}\)
We will now expand these ideas to solve a word problem using a linear equation.
Example66
When 6 is subtracted from twice the sum of a number and 8, the result is 5. Find the number.
Solution
Let \(n\) represent the unknown number. In the sentence above, "the sum of a number and 8" is represented by \(n+8\text{,}\) so "twice the sum of a number and 8" is \(2(n+8)\text{.}\) Next, "6 subtracted from twice the sum of a number and 8" would be 6 less than this, so it is \(2(n+8)-6\text{.}\) Finally, we are told that the result is 5; in other words, this expressions is equal to 5:
\begin{equation*}
2\cdot (n+8)-6=5
\end{equation*}
Now that we have translated the problem into a linear equation, we can solve for \(n\text{:}\)
\begin{equation*}
\begin{aligned}
2(n+8)-6 \amp = 5\\
2n+16-6\amp = 5\\
2n+10\amp =5\\
2n\amp = -5\\
n\amp = -\frac{5}{2}
\end{aligned}
\end{equation*}
We should always check our answer to be sure that we didn't make a mistake in setting up or solving the problem. The sum of \(-\frac{5}{2}\) and \(8\) is \(-\frac{5}{2}+8=\frac{11}{2}\text{.}\) Twice this is \(\frac{11}{2}\cdot2=11\text{,}\) and \(6\) less than this is \(5\text{.}\) Since we got the desired result, we know that our answer is correct. The unknown numbers is \(-\frac{5}{2}\text{.}\)
General guidelines for setting up and solving word problems follow:
Guidelines for Word Problems
- Read the problem several times, identify the key words and phrases, and organize the given information.
- Identify the variables by assigning a letter or expression to the unknown quantities.
- Translate and set up an algebraic equation that models the problem.
- Solve the resulting algebraic equation.
- Finally, answer the question in sentence form and make sure it makes sense (check it).
All of the equations in the following examples can be set up using only one variable. We can avoid two variables by looking for a relationship between the unknowns.
Example67
A rectangle has a perimeter measuring \(92\) meters. The length is \(2\) meters less than \(3\) times the width. Find the dimensions of the rectangle.
Solution
The sentence "The length is \(2\) meters less than \(3\) times the width" gives us the relationship between the two important quantities, the length and the width. Let \(w\) represent the width of the rectangle. Since the length is \(2\) meters less than \(3\) times the width, the length must be \(3w-2\text{.}\)
The sentence "A rectangle has a perimeter measuring \(92\) meters" suggests an algebraic set up. The perimeter of a rectangle is always the sum of twice the length and twice the width; in this example, this means that the perimeter is
\begin{equation*}
2w+2(3w-2)
\end{equation*}
Since we know that the perimeter is \(92\) meters, we have the following equation:
\begin{equation*}
92=2w+2(3w-2)
\end{equation*}
Once you have set up an algebraic equation with one variable, solve for the width, \(w\text{.}\)
\begin{equation*}
\begin{aligned}
92\amp =2w+2(3w-2) \amp \text{Distribute}\\
92\amp =2w+6w-4 \amp\text{Combine like terms}\\
92\amp =8w-4 \amp\text{Solve for }w\\
96\amp =8w\\
12\amp =w\\
\end{aligned}
\end{equation*}
Now that we know the width, we can use the fact that the length is \(3w-2\) to find the length.
\begin{equation*}
3w-2=3(\alert{12})-2=36-2=34
\end{equation*}
This means that the dimensions of the rectangle are \(12\) meters by \(34\) meters. To check, we make sure the perimeter is actually \(92\) meters:
\begin{equation*}
2(12)+2(34)=24+68=92
\end{equation*}
For the rest of this section, we will explore several different categories of application problems that you might see, such as applications of interest, currency, distances, and more.
SubsectionInterest Applications
In problems involving simple interest, it is often helpful to use the simple interest formula \(I=prt\) where \(I\) is the simple interest earned on a principle investment, \(p\text{,}\) with an interest rate of \(r\) over \(t\) years.
Example68
Given a \(4.375\)% annual interest rate, how long will it take \($2,500\) to yield \($437.50\) in simple interest?
Solution
Let \(t\) represent the time needed to earn $\(437.50\) at \(4.375\)%. Organize the information needed to use the formula for simple interest, \(I=prt\text{.}\)
| Given interest for the time period | \(I=\) $\(437.50\) |
| Given principal | \(p=\) $\(2,500\) |
| Given rate | \(r=4.375\text{%}=0.04375\) |
Next, substitute all of the known quantities into the formula and then solve for the only unknown, \(t\text{.}\)
\begin{equation*}
\begin{aligned}
I\amp = prt\\
\alert{437.50}\amp = \alert{2500}(\alert{0.04375})t\\
437.50\amp = 109.375t\\
\frac{437.50}{109.375}\amp = \frac{109.375t}{109.375}\\
4\amp = t
\end{aligned}
\end{equation*}
It takes \(4\) years for \($2,500\) invested at \(4.375\)% to earn \($437.50\) in simple interest.
Example69
Stephanie invested her total savings of \($12,500\) in two accounts earning simple interest. Her mutual fund account earned \(7\)% last year and her CD earned \(4.5\)%. If her total interest for the year was \($670\text{,}\) how much was in each account?
Solution
The sum of the money in each account is \($12,500\text{.}\) When a total is involved, a common technique used to avoid two variables is to represent the second unknown as the difference of the total and the first unknown.
Let \(m\) represent the amount invested in the mutual fund.
Since the amount in the two accounts total \($12,500\text{,}\) the amount in the CD must be \(12,500-m\text{.}\)
| Interest earned in the mutual fund (in dollars) |
\begin{align*}
I\amp = prt\\
\amp = m\cdot 0.07\cdot 1\\
\amp =0.07m
\end{align*}
|
| Interest earned in the CD (in dollars) |
\begin{align*}
I\amp = prt\\
\amp = (12,500-m)\cdot 0.045\cdot 1\\
\amp = 0.045(12,500-m)
\end{align*}
|
| Total Interest | \($670\) |
The total interest is the sum of the interest earned from each account.
\begin{equation*}
\begin{aligned}
\text{mutual fund interest}+\text{CD interest} \amp = \text{total interest}\\
0.07m +0.045(12,500-m)\amp = 670
\end{aligned}
\end{equation*}
This equation models the problem with one variable. Solve for \(m\text{.}\)
\begin{equation*}
\begin{aligned}
0.07m+0.045(12,500-m)\amp = 670\\
0.07m+562.5-0.045m\amp = 670\\
0.025m+562.5\amp = 670\\
0.025m\amp = 107.5\\
m\amp = \frac{107.5}{0.025}\\
m\amp =4,300
\end{aligned}
\end{equation*}
Use \(12,500-m\) to find the amount in the CD.
\begin{equation*}
12,500-m=12,500-\alert{4300}=8,200
\end{equation*}
Stephanie invested \($4,300\) at \(7\)% in a mutual fund and \($8,200\) at \(4.5\)% in a CD.
SubsectionCurrency Applications
A new kind of problem we come across in applications is something we call currency problems. These problems involve finding the number of coins or bills given other information about value. It is important to be careful in defining our variables specifically - either for the number of currency or the value of the currency.
Example70
Ashley has $17.25 in her piggy bank, which has only quarters and fifty-cent pieces in it. Ashley has nine more fifty-cent pieces than she has quarters. How many coins of each denomination does she have?
Solution
Let \(q\) represent the number of quarters. Since Ashley has nine more fifty-cent pieces than quarters, the number of fifty cent pieces she has is \(q+9\text{.}\)
Since a quarter is worth \($0.25\text{,}\) \(0.25q\) represents the value of Ashley's quarters. Similarly, since a fifty-cent piece is worth \($0.50\text{,}\) \(0.50(q+9)\) gives the value of Ashley's fifty-cent pieces.
Since Ashley has a total of \($17.25\text{,}\) it must be the case that the sum of these values is \(17.25\text{:}\)
\begin{equation*}
0.25q+0.50(q+9)=17.25
\end{equation*}
We can now solve for \(q\text{:}\)
\begin{equation*}
\begin{aligned}
0.25q+0.50(q+9) \amp= 17.25 \\
0.25q+0.50q+4.50 \amp= 17.25 \\
0.75q+4.50 \amp= 17.25 \\
0.75q \amp= 12.75 \\
q \amp= 17
\end{aligned}
\end{equation*}
Ashley has \(17\) quarters, and therefore \(26\) fifty-cent pieces.
SubsectionMixing Applications
Mixture problems often include a percentage and some total amount. It is important to make a distinction between these two types of quantities. For example, if a problem states that a 10-ounce container is filled with a \(3\)% saline (salt) solution, then this means that the container is filled with a mixture of salt and water as follows:
| \(\) | \(Percentage\) | \(Amount\) |
| \(Salt\) | \(3\)%\(=0.03\) | \(0.03\) (\(10\) ounces)\(=0.3\) ounces |
| \(Water\) | \(97\)%\(=0.97\) | \(0.97\) (\(10\) ounces)\(=9.7\) ounces |
In other words, we multiply the percentage times the total to get the amount of each part of the mixture.
Example72
How many milliliters of a \(15\)% alcohol solution must be mixed with \(110\) milliliters of a \(35\)% solution to obtain a \(25\)% solution?
Solution
It is often helpful to use a table to organize your work for application problems. We will use the following table to keep track of all the different solutions in this problem:
| Solution | Percent Alcohol | Total Amount of Liquid | Amount of Alcohol |
| \(15\)% solution | |||
| \(35\)% solution | |||
| Mixture |
Let \(m\) be the milliliters of the \(15\)% solution. To get the amount of alcohol in this part of the mixture, we multiply the percentage by the amount: \(0.15m\text{.}\)
Likewise, to get the amount of the second part of the mixture, we multiply the percentage by the amount: \(0.35\cdot 110=38.5\text{.}\)
Let's now think about the mixture of these two solutions. We know that we're aiming for a \(25\)% solution. Since there are \(m\) milliliters from the first solution and \(110\) milliliters from the second solution, the mixture will have \(m+110\) milliliters in it. Again, we find the amount of alcohol in the mixture by multiplying the percentage by the amount: \(0.25(m+110)\text{.}\) We can now fill in our table.
| Solution | Percent Alcohol | Total Amount of Liquid | Amount of Alcohol |
| \(15\)% solution | \(15\)%\(=0.15\) | \(m\) mL | \(0.15(m\) mL\()=0.15m\) mL |
| \(35\)% solution | \(35\)%\(=0.35\) | \(110\) mL | \(0.35(110\) mL\()=38.5\) mL |
| Mixture | \(25\)%\(=0.25\) | \(m+110\) mL | \(0.25(m+110)\) mL |
From our table, we see that the total amount of alcohol in the mixture is \(0.25(m+110)\text{.}\) On the other hand, we know that there are \(0.15m\) milliliters from the first solution and \(38.5\) milliliters from the second solution, for a total of \(0.15m+38.5\) milliliters of alcohol in the solution. We have found two different expressions for the total amount of alcohol in the mixture, so they must be equal:
\begin{equation*}
0.15m+38.5 = 0.25(m+110)
\end{equation*}
We can now solve for \(m\text{.}\)
\begin{equation*}
\begin{aligned}
0.15m+38.5\amp = 0.25(m+110)\\
0.15m +38.5 \amp =0.25m+27.5\\
38.5\amp = 0.10m+27.5\\
11\amp =0.10m\\
110\amp =m
\end{aligned}
\end{equation*}
We have found that we must mix \(110\) milliliters of a \(15\)% alcohol solution with \(110\) milliliters of a \(35\)% solution to obtain a \(25\)% solution.
SubsectionDistance Applications
The distance traveled is equal to the average rate times the time traveled at that rate, \(d=r\cdot t\text{.}\) These problems usually have a lot of data, so it helps to carefully rewrite the pertinent information as you define variables.
Example73
Two planes leave a city traveling in opposite directions. One travels at a rate of \(530\) mph and the other at a rate of \(600\) mph. How long will it take until they are \(3672.5\) miles apart?
Solution
Let \(d_1\) represent the distance travelled by the first plane in miles, and let \(d_1\) represent the distance travelled by the second plane in miles. The key to this problem is that the sum of their distances is the distance between them:
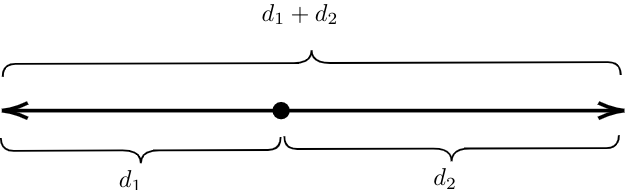
Let \(t\) represent the time it takes for them to be \(3672.5\) miles apart (in hours); this is what we're actually looking for. The first plane travels at a rate of \(530\) mph, meaning that its distance is modeled by the equation
\begin{equation*}
d_1=r\cdot t= 530 t
\end{equation*}
The second plane travels at a rate of \(600\) mph, meaning that its distance is modeled by the equation
\begin{equation*}
d_2=r\cdot t= 600 t
\end{equation*}
Since the sum of their distances is the distance between them, after \(t\) hours the two planes will be
\begin{equation*}
d_1+d_2=530t+600t=1130t
\end{equation*}
miles apart. Now, we want to know when the distance is \(3672.5\text{.}\) Thus we solve:
\begin{equation*}
\begin{aligned}
3672.5\amp =1130t\\
3.25\amp =t
\end{aligned}
\end{equation*}
This tells us that it will take \(3\) hours and \(15\) minutes for the planes to be \(3672.5\) miles apart.