In the previous chapter, we explored many properties of linear equations and the graphs that represent their solution sets. Real-world applications are often modeled using more than one equation. In this chapter, we will look at how to find solutions that are solutions for multiple linear equations simultaneously and think about the graphical meaning of these solutions.
define a system of linear equations and learn what it means to be a solution of a system of linear equations
find solution(s) of a system of linear equations using graphs, the substitution method, and the elimination method.
The main topics of this section are also presented in the following videos:
A system of equations consists of a set of two or more equations with the same variables. In this section, we will study linear systems consisting of two linear equations each with two variables. The system
is one such system.
A solution to a linear system, or simultaneous solution, is an ordered pair \((x, y)\) that solves both of the equations. In this case, \((3,2)\) is the only solution. To check that an ordered pair is a solution, substitute the corresponding \(x\)- and \(y\)-values into each equation and then simplify to see if you obtain a true statement for both equations.
| Check: \((3,2)\) | |
| Equation 1: \(2x-3y=0\) | Equation 2: \(-4x+2y=-8\) |
\begin{align*}
2(\alert{3})-3(\alert{2})\amp =0\\
6-6\amp =0\\
0\amp =0
\end{align*}
|
\begin{align*}
-4(\alert{3})+2(\alert{2})\amp =-8\\
-12+4\amp =-8\\
-8\amp =-8
\end{align*}
|
Determine whether or not \((1,0)\) is a solution to the system \(\begin{cases} x-y\amp =1\\ -2x+3y\amp =5\\ \end{cases} \text{.}\)
Substitute the appropriate values into both equations.
| Check: \((1,0)\) | |
| Equation 1: \(x-y=1\) | Equation 2: \(-2x+3y=5\) |
\begin{align*}
(\alert{1})-(\alert{0})\amp =1\\
1-0\amp =1\\
1\amp =1
\end{align*}
|
\begin{align*}
-2(\alert{1})+3(\alert{0})\amp =5\\
-2+0\amp =5\\
-2\amp = 5
\end{align*}
|
Notice that when we check \((1,0)\) in Equation 2, we get a false statement, \(-2=5\text{.}\) Although \((1,0)\) satisfies Equation 1, it does not satisfy Equation 2, so \((1,0)\) is not a solution to this system.
Determine whether or not \((-2,4)\) is a solution to the system \(\begin{cases} x-y\amp =-6\\ -2x+3y\amp =16\\ \end{cases} \text{.}\)
Substitute the appropriate values into both equations.
| Check: \((-2,4)\) | |
| Equation 1: \(x-y=-6\) | Equation 2: \(-2x+3y=16\) |
\begin{align*}
(\alert{-2})-(\alert{4}) \amp= -6\\
-2-6 \amp= -6\\
-6 \amp= -6
\end{align*}
|
\begin{align*}
-2(\alert{-2})+3(\alert{4}) \amp= 16\\
4 + 12 \amp= 16\\
16 \amp= 16
\end{align*}
|
The point \((-2,4)\) is a solution to both equations, therefore it is a solution to this system of equations.
Geometrically, a linear system of equations consists of two lines, where a solution is a point of intersection. To illustrate this, we will graph the following system of linear equations:
First, we will rewrite the equations in slope-intercept form so that we may easily graph them.
First Equation:
Second Equation:
Next, replace these forms of the original equations in the system to obtain what is called an equivalent system. Two systems of equations are equivalent if they share the same solution set.
If we graph both of the lines on the same set of axes, then we can see that the point of intersection is \((3, 2)\text{.}\) This means that the solution to this system is \((3,2)\)
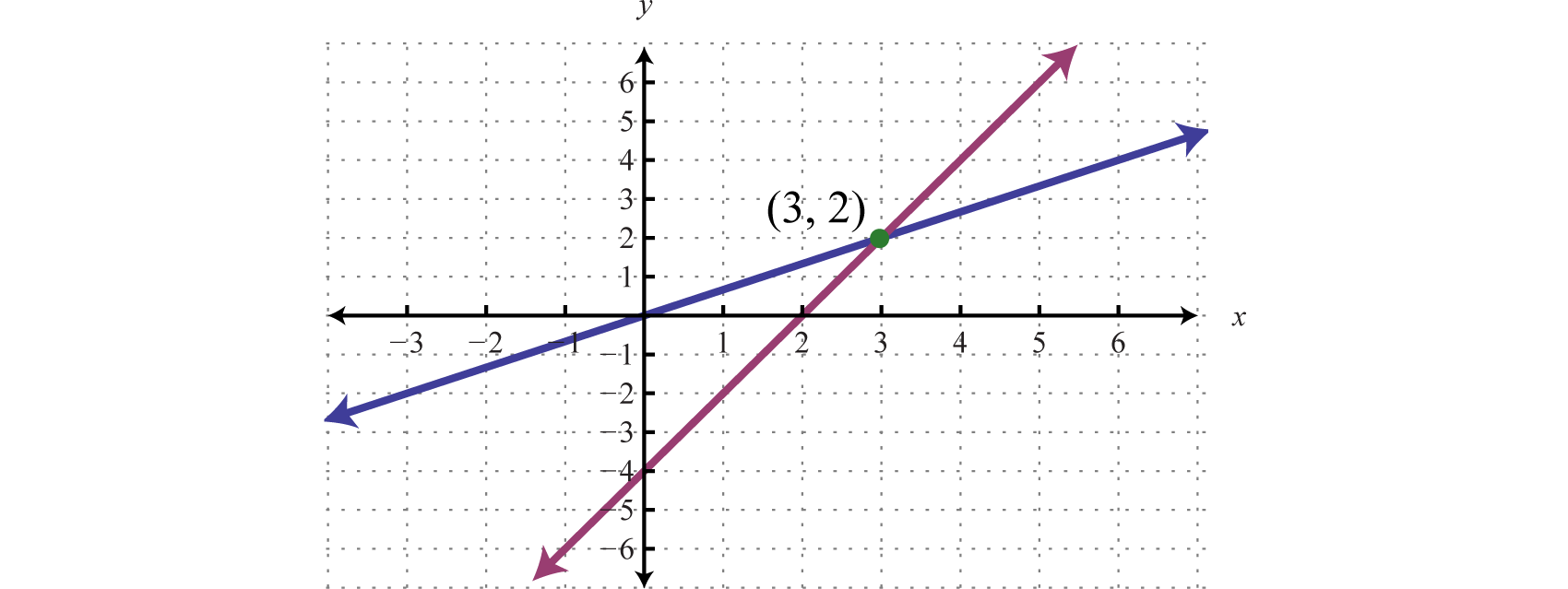
To summarize, linear systems described in this section consist of two linear equations, each with two variables. A solution is an ordered pair that corresponds to a point where the two lines intersect in the rectangular coordinate plane. Therefore, one way to solve linear systems is by graphing both lines on the same set of axes and determining the point where they cross. This describes the graphing method for solving linear systems.
Solve the system of equations by graphing it: \(\begin{cases} x-y\amp =-4\\ 2x+y\amp =1 \end{cases}\)
Rewrite the linear equations in slope-intercept form.
First Equation:
Second Equation:
Write the equivalent system and graph the lines on the same set of axes.
\begin{gather*}
\alert{\text{Line 1: }}\, y=x+4\\
y\text{-intercept: }\, (0,4)\\
\text{slope: }m=1=\frac{1}{1}=\frac{\text{rise}}{\text{run}}
\end{gather*}
|
\begin{gather*}
\alert{\text{Line 2: }}\, y=-2x+1\\
y\text{-intercept: }\, (0,1)\\
\text{slope: }m=-2=\frac{-2}{1}=\frac{\text{rise}}{\text{run}}
\end{gather*}
|
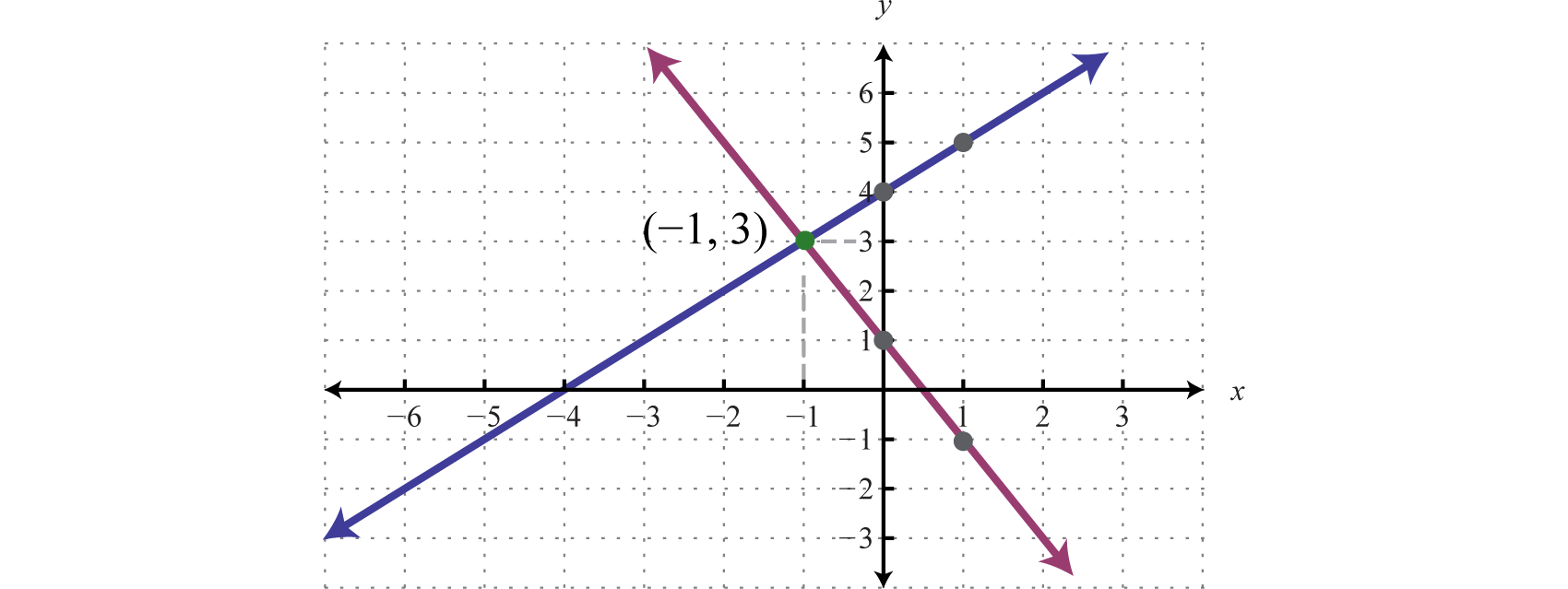
We use the graph to estimate the point where the lines intersect and check to see if it solves the original system. In the above graph, the point of intersection appears to be \((-1, 3)\text{.}\)
| Check: \((-1,3)\) | |
| Line 1: \(x-y=-4\) | Line 2: \(2x+y=1\) |
\begin{align*}
(\alert{-1})-(\alert{3})\amp =-4\\
-1-3\amp =-4\\
-4\amp =-4
\end{align*}
|
\begin{align*}
2(\alert{-1})+(\alert{3})\amp =1\\
-2+3\amp =1\\
1\amp =1
\end{align*}
|
The solution is \((-1,3)\text{.}\)
Solve the system of equations by graphing it.: \(\begin{cases} 2x+y\amp =2\\ -2x+3y\amp =-18 \end{cases}\text{.}\)
We first rewrite the linear equations in slope-intercept form.
Now we graph the lines and determine the point of intersection.
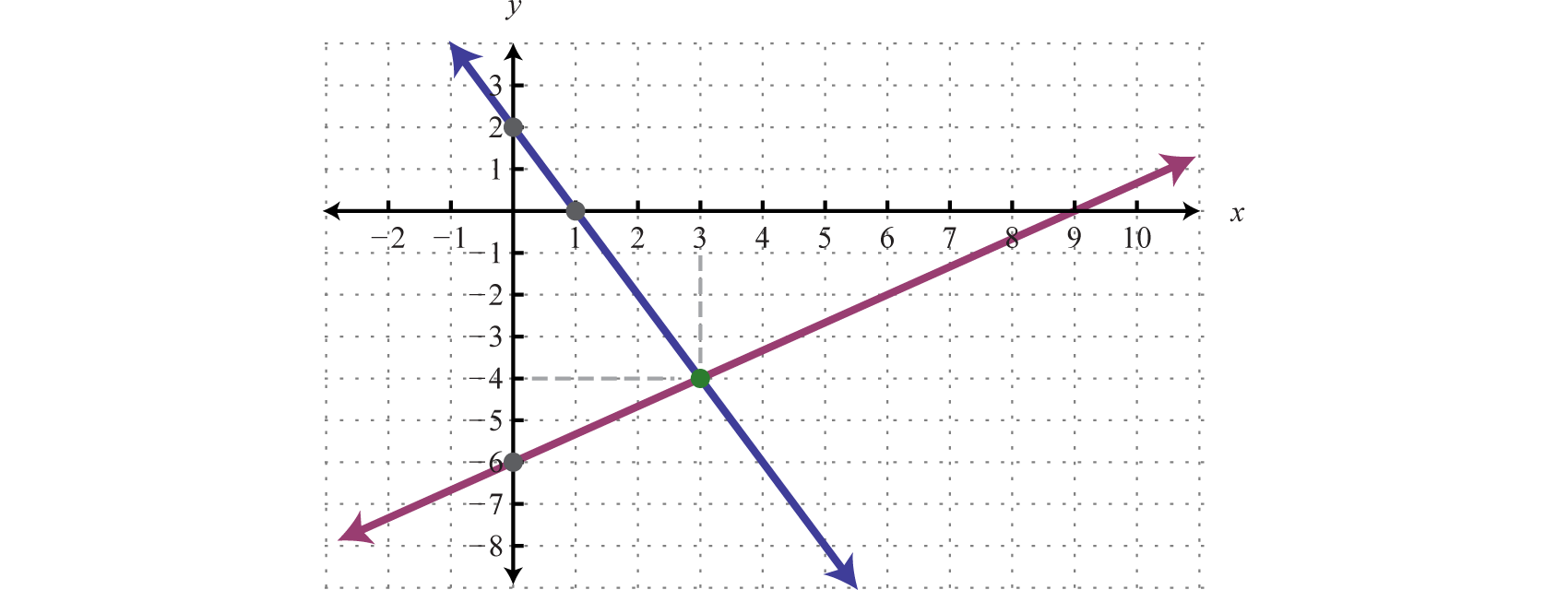
We use the graph to estimate the point where the lines intersect and check to see if it solves the original system. In the above graph, the point of intersection appears to be \((3, -4)\text{.}\)
| Check: \((3,-4)\) | |
| Line 1: \(2x+y=2\) | Line 2: \(-2x+3y=-18\) |
\begin{align*}
2(\alert{3})+(\alert{-4})\amp =2\\
6-4\amp =2\\
2\amp =2
\end{align*}
|
\begin{align*}
-2(\alert{3})+3(\alert{-4})\amp =-18\\
-6-12\amp =-18\\
-18\amp =-18
\end{align*}
|
The solution is \((3,-4)\text{.}\)
Solve the system of equations by graphing it.: \(\begin{cases} 3x+y\amp =6\\ y\amp =-3 \end{cases}\text{.}\)
We first rewrite the linear equations in slope-intercept form.
Now we graph the lines and determine the point of intersection.
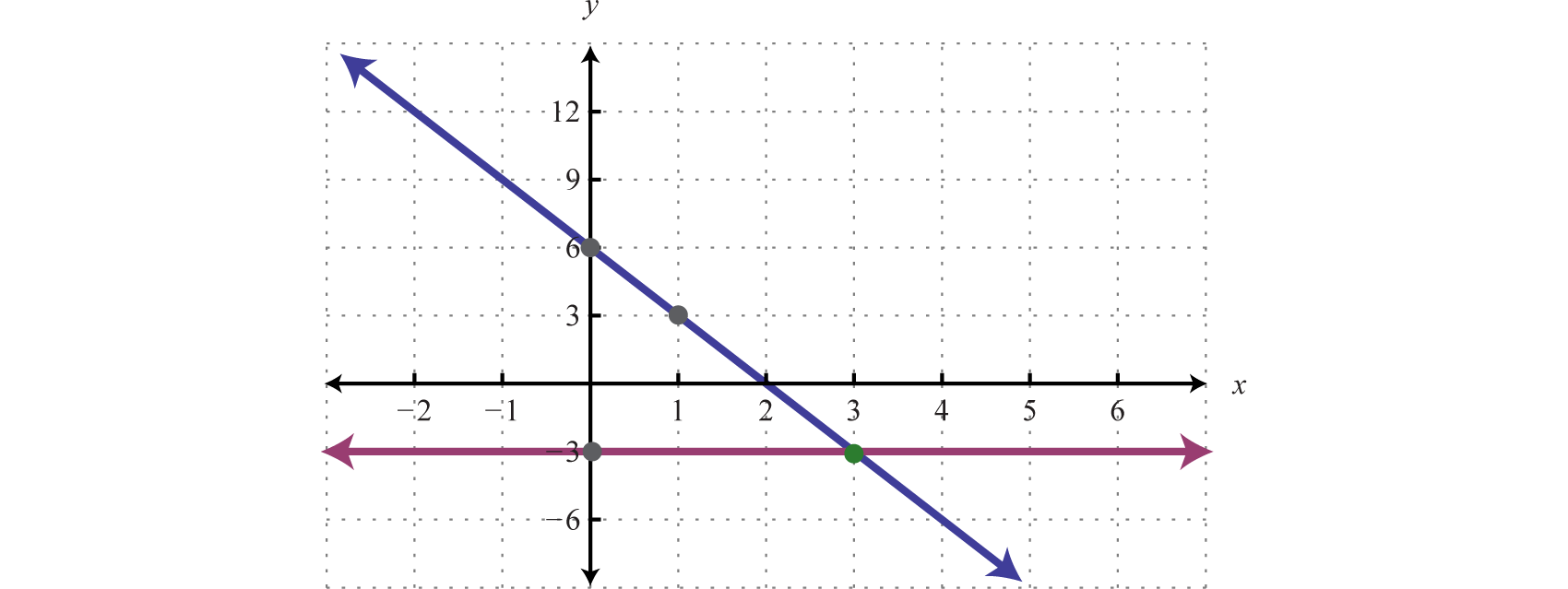
We use the graph to estimate the point where the lines intersect and check to see if it solves the original system. In the above graph, the point of intersection appears to be \((3, -3)\text{.}\)
| Check: \((3,-3)\) | |
| Line 1: \(-3x+y=6\) | Line 2: \(y=-3\) |
\begin{align*}
3(\alert{3})+(\alert{-3})\amp =6\\
9-3\amp =6\\
6\amp =6
\end{align*}
|
\begin{align*}
(\alert{-3})\amp=-3\\
-3\amp =-3
\end{align*}
|
The solution is \((3,-3)\text{.}\)
The graphing method for solving linear systems is not ideal when a solution consists of coordinates that are not integers. The goal of the graphing method is to understand the geometry involved when solving systems. It is important to remember that the solutions to a system correspond to the point, or points, where the graphs of the equations intersect.
In this section, we review a completely algebraic technique for solving systems, the substitution method. The idea is to solve one equation for one of the variables and substitute the result into the other equation. After performing this substitution step, we are left with a single equation with one variable, which can be solved using algebra.
Solve by substitution: \(\begin{cases} 2x+y\amp =-3\\ 3x-2y\amp =-8 \end{cases}\text{.}\)
We can solve for either variable in either equation. If we choose the first equation, we can isolate \(y\) in one step.
Substitute the expression \(-2x-3\) for the variable \(y\) in the other equation.
This leaves us with an equivalent equation with one variable, which can be solved using the techniques learned up to this point. Solve for the remaining variable.
Use this value to find the other coordinate. Substitute \(x = -2\) into either of the original equations or their equivalents. Typically, we use the equivalent equation that we found when isolating a variable in the first step.
Remember to present the solution as an ordered pair: \((-2,1)\text{.}\) Verify that these coordinates solve both equations of the original system:
| Check: \((-2,1)\) | |
| Line 1: \(2x+y=-3\) | Line 2: \(3x-2y=-8\) |
\begin{align*}
2(\alert{-2})+(\alert{1})\amp =-3\\
-4+1\amp =-3\\
-3\amp =-3
\end{align*}
|
\begin{align*}
3(\alert{-2})-2(\alert{1})\amp=-8\\
-6-2\amp =-8\\
-8\amp =-8
\end{align*}
|
The graph of the linear system is given below:
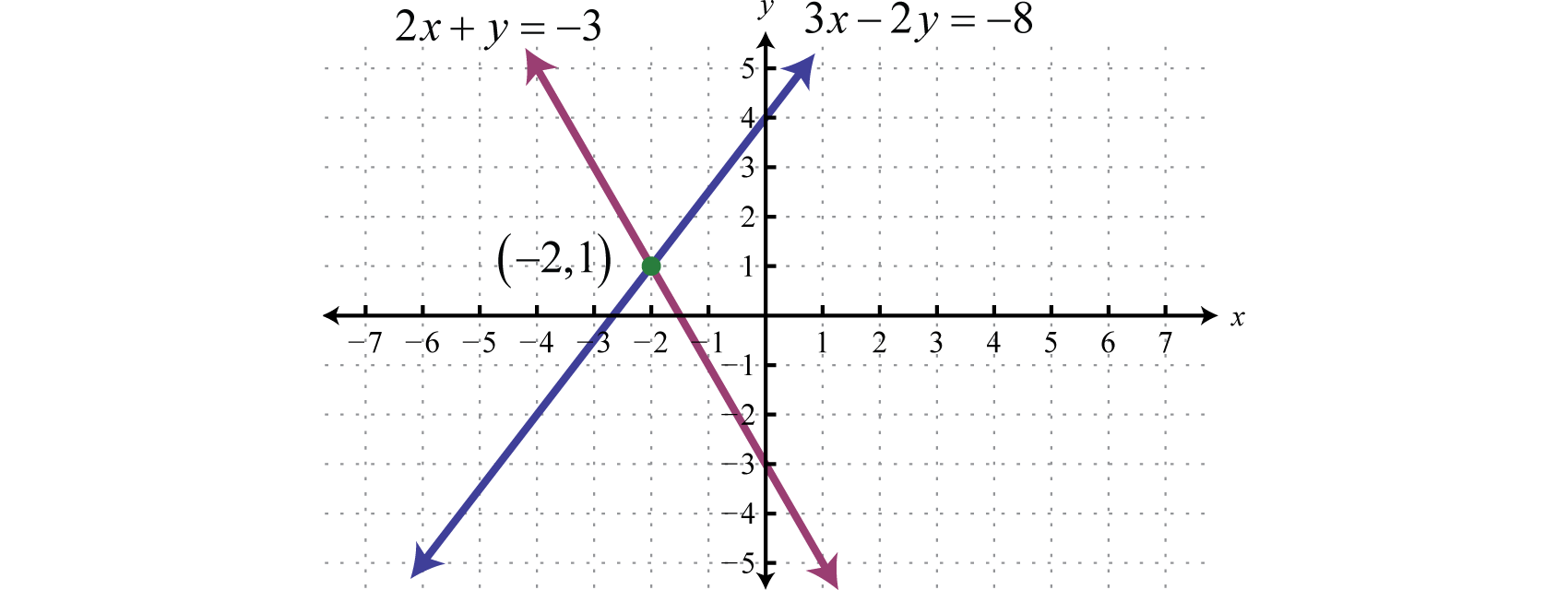
The substitution method for solving systems is a completely algebraic method. Thus graphing the lines is not required.
The solution is \((-2,1)\text{.}\)
When doing the substitution method, you must substitute one equation into the other equation. For example, if you solve Equation 1 for \(y\text{,}\) you must substitute the result into Equation 2. If you substitute back into the equation you started with, you will get a misleading result.
Solve by substitution: \(\begin{cases} 3x-5y\amp =9\\ 4x+2y\amp =-1 \end{cases}\text{.}\)
We can solve for either variable in either equation. In this case, we will begin by solving for \(x\) in the first equation.
Substitute into the other equation and solve for \(y\text{.}\)
Use this value to find the other coordinate. We will substitute into the equivalent equation that we found when isolating a variable in the first step.
The solution is \(\left(\frac{1}{2},-\frac{3}{2}\right)\text{.}\)
Solve by substitution: \(\begin{cases} 5x-4y\amp =3\\ x+2y \amp= 2 \end{cases}\)
We begin by solving the second equation for \(x\text{.}\)
Substitute into the other equation and solve for \(y\text{.}\)
Use this value to find the other coordinate. We will substitute it into the original version of the second equation.
The solution is \(\left(1,\frac{1}{2}\right)\text{.}\)
In this section, the goal is to learn another completely algebraic method for solving a system of linear equations called the elimination method. This method depends on the addition property of equations: given algebraic expressions \(a, b, c\text{,}\) and \(d\) we have
Consider the following system:
We can add the equations together to eliminate the variable \(y\text{.}\)
This leaves us with a linear equation with one variable that can be easily solved:
At this point, we have the \(x\)-coordinate of the simultaneous solution, so all that is left to do is to find the corresponding \(y\)-value. We can do this by back substituting \(x=3\) into one of the original equations:
The solution to the system is \((3, 2)\text{.}\) Of course, the variable is not always so easily eliminated. Typically, we have to find an equivalent system by applying the multiplication property of equality to one or both of the equations as a means to line up one of the variables to eliminate. The goal is to arrange so that either the \(x\) terms or the \(y\) terms are additive opposites, so that when the equations are added, the terms eliminate each other.
Solve by elimination: \(\begin{cases} 5x-3y\amp =-1\\ 3x+2y\amp =7 \end{cases}\text{.}\)
We choose to eliminate the terms with variable \(y\) because the coefficients have different signs. In order to get \(3y\) in the second equation we would have to multiply by \(\frac{3}{2}\text{.}\) If we instead wanted to multiply the first equation to have \(-2y\text{,}\) we would have to multiply it by \(\frac{2}{3}\text{.}\)
However, we can avoid using fractions at this step altogether. To do this, we first determine the least common multiple of the coefficients that we are trying to match; in this case, we are trying to eliminate the \(y\) variable so we compute \(\text{LCM}(3, 2)\text{,}\) which is \(6\text{.}\) Therefore, multiply both sides of both equations by the appropriate values to obtain coefficients of \(-6\) and \(6\text{.}\) This results in the following equivalent system:
The terms involving \(y\) are now lined up to eliminate. We add the equations together and solve for \(x\text{.}\)
This gives us \(x=1\text{.}\) Now we substitute into either one of the original equations.
This means our solution is \((1,2)\text{.}\) We can check this as follows:
| Check: \((1,2)\) | |
| Line 1: \(5x-3y=-1\) | Line 2: \(3x+2y=7\) |
\begin{align*}
5(\alert{1})-3(\alert{2})\amp =-1\\
5-6\amp =-1\\
-1\amp =-1
\end{align*}
|
\begin{align*}
3(\alert{1})+2(\alert{2})\amp=7\\
3+4\amp =7\\
7\amp =7
\end{align*}
|
Sometimes linear systems are not given in standard form \(ax+by=c\text{.}\) When this is the case, it is best to rearrange the equations before beginning the steps to solve by elimination. Also, we can eliminate either variable. The goal is to obtain a solution for one of the variables and then back substitute to find a solution for the other.
Solve by elimination: \(\begin{cases} 12x+5y\amp =11\\ 3x\amp =4y+1 \end{cases}\text{.}\)
First, we will rewrite the second equation in standard form to line up the like terms.
We can eliminate the term with variable \(x\) if we multiply the second equation by \(-4\text{.}\)
Next, we add the equations together.
Now we substitute into either one of our original equations.
The solution is \(\left(\frac{7}{9},\frac{1}{3}\right)\text{.}\)
Solve by elimination: \(\begin{cases} 2x+5y\amp =5\\ 3x+2y\amp =-9 \end{cases}\)
We will eliminate the terms with the \(y\) variable. To do this, we multiply the first equation by \(-2\) and the second equation by \(5\text{.}\)
Next, we add the equations together.
Now we substitute into either one of our original equations.
The solution is \((-5,3)\text{.}\)
Given a linear system where the equations have fractional coefficients, it is usually best to clear the fractions before beginning the elimination method.
Solve by elimination: \(\begin{cases} -\frac{1}{10}x\amp +\frac{1}{2}y\amp =\frac{4}{5}\\ \frac{1}{7}x\amp +\frac{1}{3}y\amp =-\frac{2}{21} \end{cases}\text{.}\)
We can clear fractions by multiplying both sides of an equation by the least common multiple of the denominators. Be careful distributing, and then simplify.
First Equation:
Second Equation:
This results in an equivalent system where the equations have integer coefficients, and now we can solve using the elimination method.
This gives \(y=1\text{,}\) and now we substitute into one of our original equations or an equivalent form of one of our original equations.
The solution is \((-3,1)\text{.}\)
Solve by elimination: \(\begin{cases} \frac{1}{3}x\amp -\frac{2}{3}y\amp =3\\ \frac{1}{3}x\amp -\frac{1}{2}y\amp=\frac{8}{3} \end{cases}\)
To clear the fractions in the first equation we will multiply by \(3\text{;}\) to clear the fractions in the second equation, we multiply by \(6\text{.}\)
First equation:
Second equation:
This results in an equivalent system where the equations have integer coefficients, and now we can solve using the elimination method. We will multiply the second equation by \(-2\) to eliminate the \(x\) variable.
We now substitute \(y=-2\) into one of the original equations or an equivalent form of one of our original equations.
The solution is \((5,-2)\text{.}\)
Until this point, we have looked at examples of systems of equations that have exactly one solution. Such a solution corresponds to the single point where the graphs of these linear equations intersects. However, there are other possible types of solutions sets that a system of two linear equations can have, and these correspond to the other ways that two lines can interact graphically. The following examples illustrate the other cases that can occur with systems of two linear equations.
Solve by the following system of equations: \(\begin{cases} -5x+y\amp =-1\\ 10x-2y\amp =2 \end{cases}\)
We will use the substitution method by solving the first equation for \(y\)
Substitute into the other equation.
In this case, our variables cancelled and we ended up with a true statement. This means the equation is an identity and any real number is a solution. The solutions are of the form \((x,mx+b)\text{,}\) and specifically in this case, our solutions are \((x,5x-1)\text{,}\) where \(x\) is any real number. Since \(x\) can be any real number, there are infinitely many solutions.
To have a better understanding of the previous example, rewrite both equations in slope-intercept (\(y=mx+b\)) form and graph them on the same set of axes.
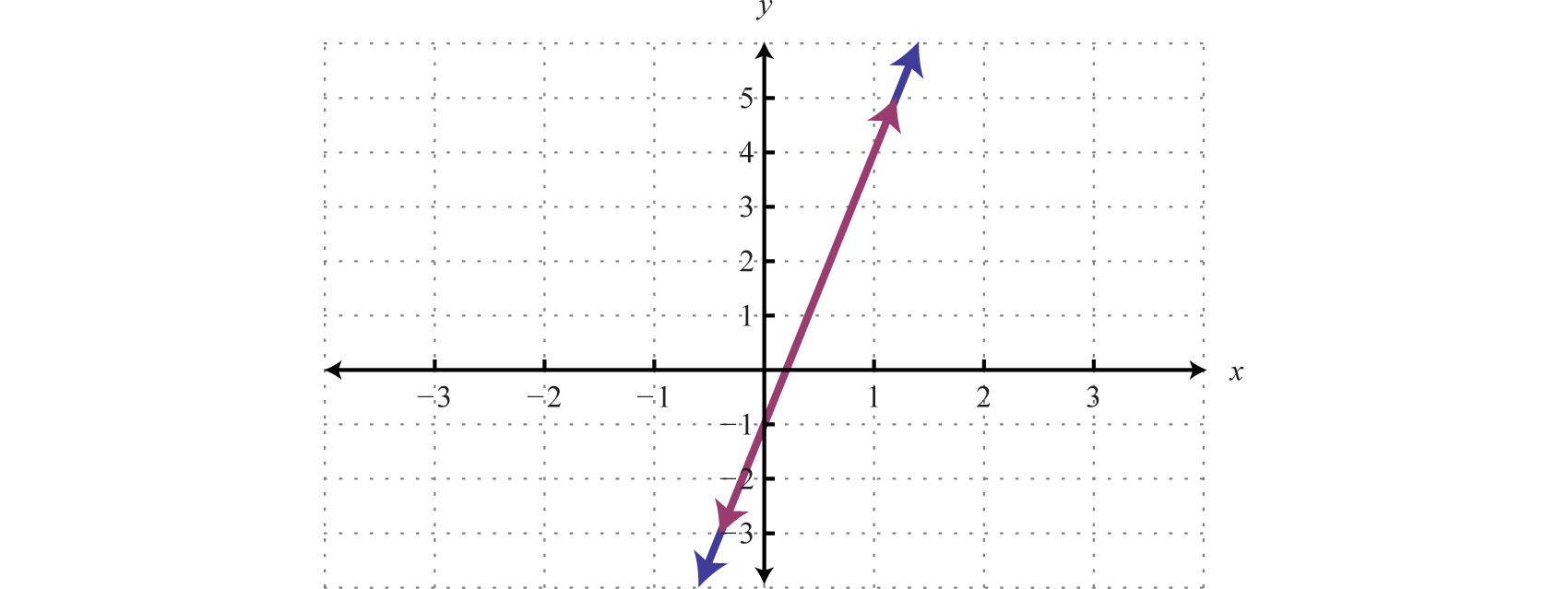
We can see now that both equations represent the same line.
Solve the following system of equations: \(\begin{cases} -7x+3y\amp =3\\ 14x-6y\amp =-16 \end{cases} \text{.}\)
We will use the elimination method by multiplying the first equation by \(2\)
In this case, our variables cancelled and we ended up with a false statement. This means the equation is a contradiction. There is no solution for \(x\) and hence no solution to the system.
A false statement indicates that the system is inconsistent, or in geometric terms, that the lines are parallel and do not intersect. To illustrate this, determine the slope-intercept form of each line and graph them on the same set of axes.
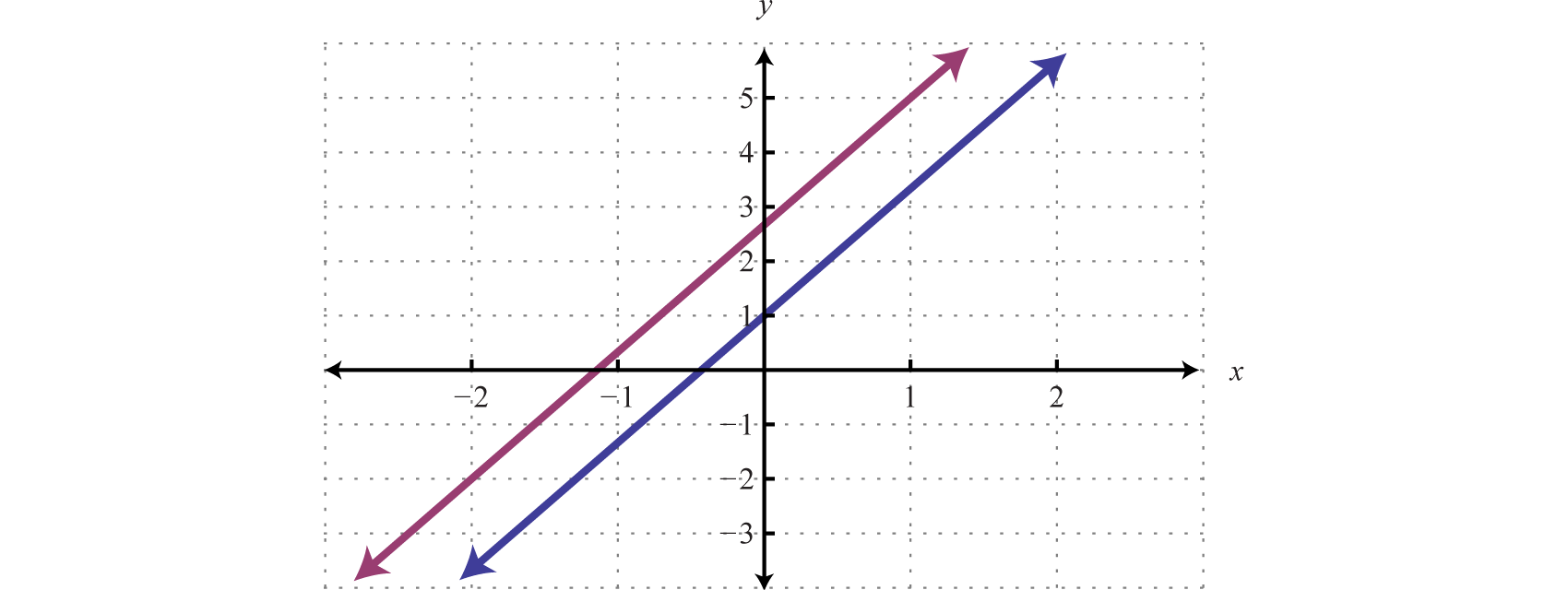
In slope-intercept form, it is easy to see that the two lines have the same slope but different y-intercepts.
We have reviewed three methods for solving linear systems of two equations with two variables. Each method is valid and can produce the same correct result. In this section, we summarize the strengths and weaknesses of each method.
The graphing method is useful for understanding what a system of equations is and what the solutions must look like. When the equations of a system are graphed on the same set of axes, we can see that the solution is the point where the graphs intersect. The graphing is made easy when the equations are in slope-intercept form. For example,
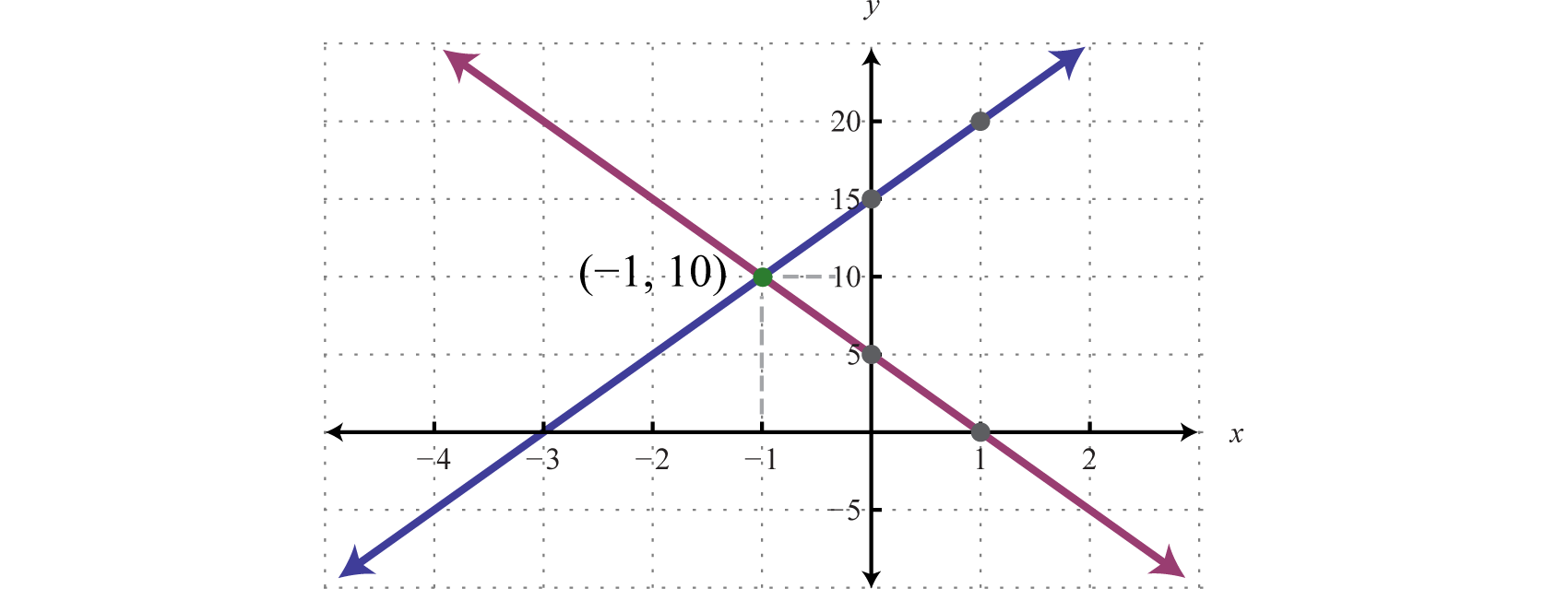
The simultaneous solution \((-1, 10)\) corresponds to the point of intersection. One drawback of this method is that it can be very inaccurate. When the coordinates of the solution are not integers, the method is practically unusable. If we have a choice, we typically avoid this method in favor of the more accurate algebraic techniques.
The substitution method, on the other hand, is a completely algebraic method. It requires you to solve for one of the variables and substitute the result into the other equation. The resulting equation has one variable for which you can solve. This method is particularly useful when there is a variable within the system with coefficient of 1. For example,
if a good candidate for substitution because we can easily solve for \(y\) in the first equation and then substitute the result into the other equation. One drawback of this method is that it often leads to equivalent equations with fractional coefficients, which are tedious to work with. If there is not a coefficient of 1, then it usually is best to choose the elimination method.
The elimination method is a completely algebraic method which makes use of the addition property of equations. We multiply one or both of the equations to obtain equivalent equations where one of the variables is eliminated if we add them together. For example,
To eliminate the terms involving \(x\text{,}\) we would multiply both sides of the first equation by 5 and both sides of the second equation by \(-2\text{.}\) This results in an equivalent system where the variable \(x\) is eliminated when we add the equations together. Of course, there are other combinations of numbers that achieve the same result. We could even choose to eliminate the variable \(y\text{.}\) No matter which variable is eliminated first, the solution will be the same. Note that the substitution method, in this case, would require tedious calculations with fractional coefficients. One weakness of the elimination method, as we will see later in our study of algebra, is that it does not always work for nonlinear systems.
