Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionInverse Trigonometric Functions
In this chapter, we have evaluated trigonometric functions at various angles, but what if we need to know what angle yields a specific sine, cosine, or tangent value? To find angles, we need inverse trigonometric functions.
SubsectionExamples with Exact Values
Example45
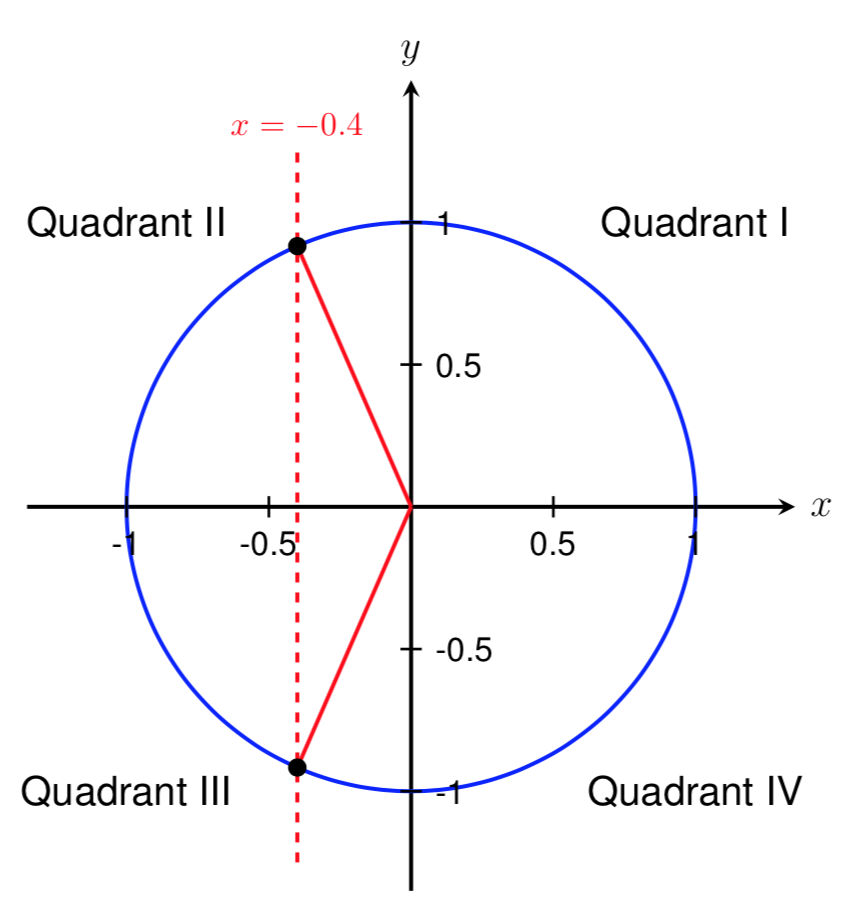
If \(\cos(\theta)=-0.4\text{,}\) in which quadrants can \(\theta\) lie?
Solution
Since our cosine value is negative and cosine corresponds to the \(x\) coordinate of a point on the unit circle, \(\theta\) could lie in Quadrant II or Quadrant III.
In the previous example, we were given a trigonometric value and could use the definition of cosine to determine the quadrants in which \(\theta\) could lie. However, in order to solve for \(\theta\text{,}\) we need an additional tool.
Inverse Sine, Cosine, and Tangent Functions
If \(\sin(\theta)=a\text{,}\) then \(\sin^{-1}(a)=\theta\)
If \(\cos(\theta)=a\text{,}\) then \(\cos^{-1}(a)=\theta\)
If \(\tan(\theta)=a\text{,}\) then \(\tan^{-1}(a)=\theta\)
Note that the output of each of these inverse functions is an angle.
Note46Common Notation
The inverse sine function, \(\sin^{-1}(a)\) is sometimes called the arcsine function, and notated \(\arcsin(a)\text{.}\)
The inverse cosine function, \(\cos^{-1}(a)\) is sometimes called the arccosine function, and notated \(\arccos(a)\text{.}\)
The inverse tangent function, \(\tan^{-1}(a)\) is sometimes called the arctangent function, and notated \(\arctan(a)\text{.}\)
Caution47
Based only on the definitions above, the inverse trigonometric functions are not actually functions at all! For example, since \(\sin(0)=0\) and \(\sin(2\pi)=0\text{,}\) we have that \(\sin^{-1}(0)=0\) and \(\sin^{-1}(0)=2\pi\text{.}\)
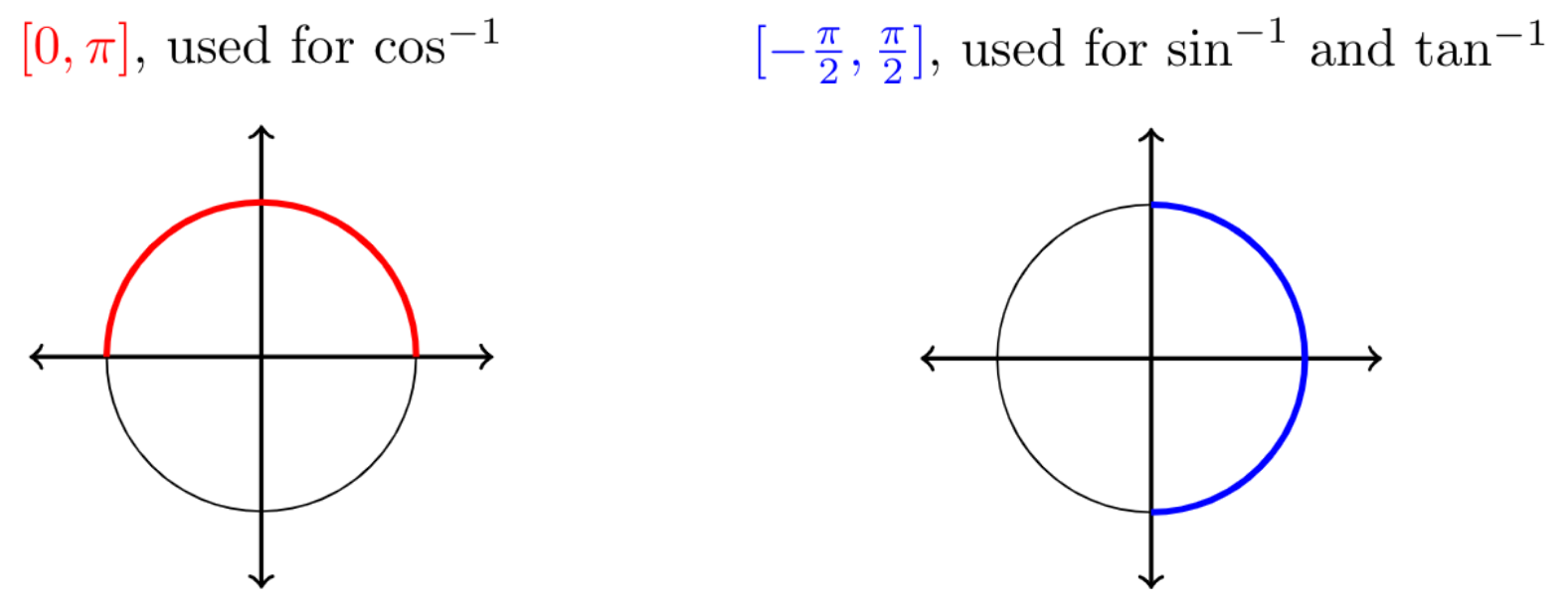
This can be fixed by restricting the outputs to a certain interval. For example, most calculators will give an output for \(\cos^{-1}\) in the interval \([0,\pi]\text{,}\) but will give an output for \(\sin^{-1}\) and \(\tan^{-1}\) in the interval \([-\frac{\pi}{2},\frac{\pi}{2}]\text{.}\)
Example48
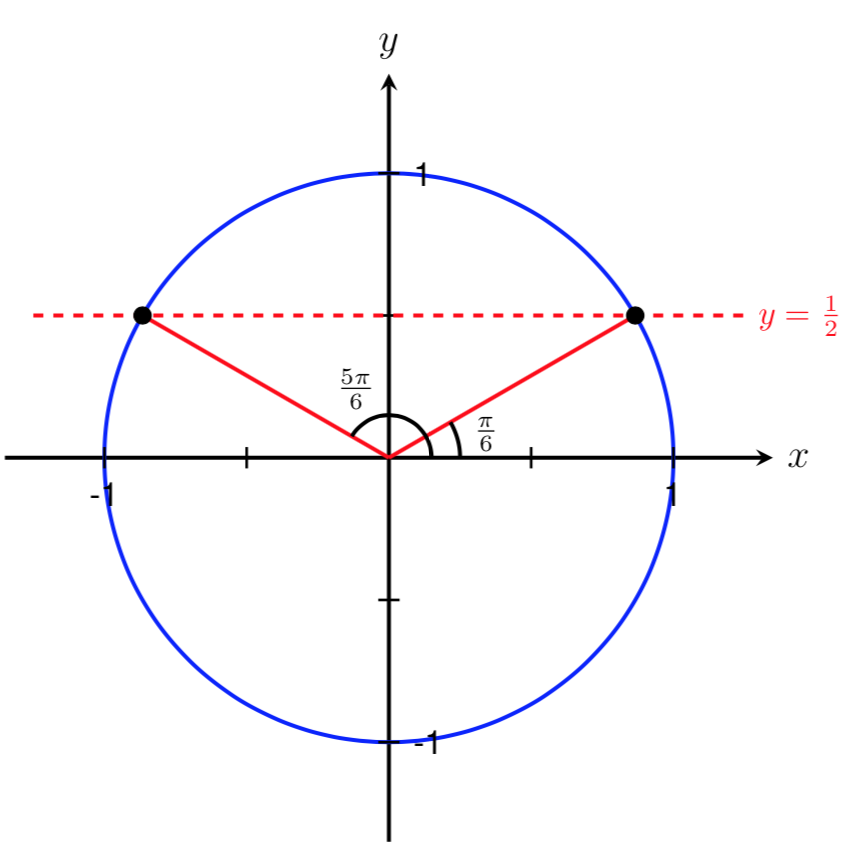
Find two angles in the interval \([0,2\pi]\) such that \(\displaystyle \sin(\theta)=\frac{1}{2}\text{.}\)
Solution
Since we are given a sine value, we know that we are looking for angles with a \(y\) coordinate of \(1/2\) on the unit circle.
From the common angles on the unit circle, the two angles where \(\sin(\theta)=1/2\) in the interval \([0,2\pi]\) are
\begin{equation*}
\theta = \frac{\pi}{6} \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{5\pi}{6}
\end{equation*}
Example49
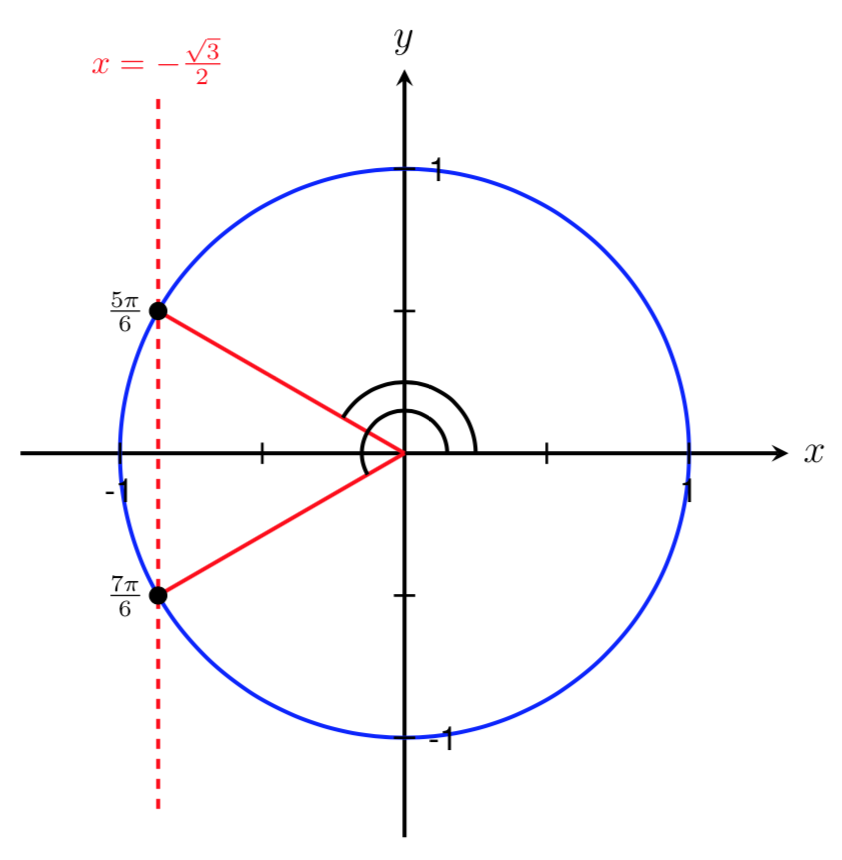
Find two angles in the interval \([0,2\pi]\) such that \(\displaystyle \cos(\theta)=-\frac{\sqrt{3}}{2}\text{.}\)
Solution
Since we are given a cosine value, we know that we are looking for angles with an \(x\) coordinate of \(-\sqrt{3}/2\) on the unit circle.
From the common angles on the unit circle, the two angles where \(\cos(\theta)=-\sqrt{3}/2\) in the interval \([0,2\pi]\) are
\begin{equation*}
\theta = \frac{5\pi}{6} \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{7\pi}{6}
\end{equation*}
Example50
Find two angles in the interval \([0,2\pi]\) such that \(\tan(\theta)=1\text{.}\)
Solution
Since we are given a tangent value of 1 and \(\tan(\theta) = y/x\text{,}\) we know that we are looking for angles where the \(x\) and \(y\) values are equal on the unit circle.
From the common angles on the unit circle, the two angles where the \(x\) and \(y\) values are equal and \(\tan(\theta)=1\) in the interval \([0,2\pi]\) are
\begin{equation*}
\theta = \frac{\pi}{4} \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{5\pi}{4}
\end{equation*}
Example51
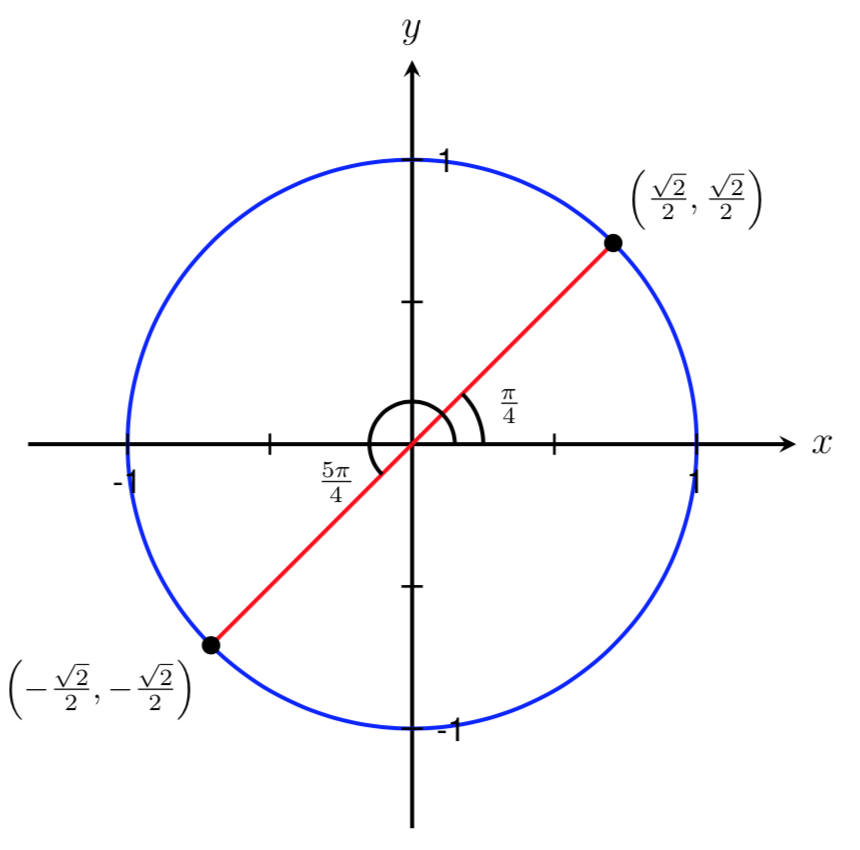
Find all angles in the interval \(\displaystyle [0,2\pi]\) such that
\begin{equation*}
\displaystyle \text{a.} \hspace{.1in} \sin(\theta)=-1 \hspace{.5in} \text{b.} \hspace{.1in} \cos(\theta)=\frac{\sqrt{2}}{2} \hspace{.5in} \text{c.} \hspace{.1in} \tan(\theta)=\sqrt{3}
\end{equation*}
Solution
- Since we are given a sine value of \(-1\text{,}\) we know that we are looking for angles where the \(y\) value is equal to \(-1\text{.}\) The only such angle in the interval \(\displaystyle [0,2\pi]\) is \(\theta=\frac{3\pi}{2}\text{.}\)
- Since we are given a cosine value of \(\frac{\sqrt{2}}{2}\text{,}\) we are looking for angles where the \(x\) value is equal to \(\frac{\sqrt{2}}{2}\text{.}\) From the common angles on the unit circle, the two angles in the interval \(\displaystyle [0,2\pi]\) are\begin{equation*} \frac{\pi}{4} \hspace{.25in} \text{ and } \hspace{.25in} \frac{7\pi}{4} \end{equation*}
-
This time we are looking for angles such that
\begin{equation*} \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}=\sqrt{3} \end{equation*}Since
\begin{equation*} \sqrt{3}=\frac{\sqrt{3}/2}{1/2}=\frac{-\sqrt{3}/2}{-1/2} \end{equation*}the two such angles are \(\frac{\pi}{3}\) (which corresponds to \(\sin(\theta)=\sqrt{3}/2\) and \(\cos(\theta)=1/2\)) and \(\frac{4\pi}{3}\) (which corresponds to \(\sin(\theta)=-\sqrt{3}/2\) and \(\cos(\theta)=-1/2\)).
SubsectionMore Examples with Non-Exact Values
In the previous examples and exercises, we were able to use the unit circle to solve for \(\theta\text{,}\) but if we are given trigonometric values that do not correspond to common angles on the unit circle, we will need to use a calculator to find approximate values for \(\theta\text{.}\)
Example52
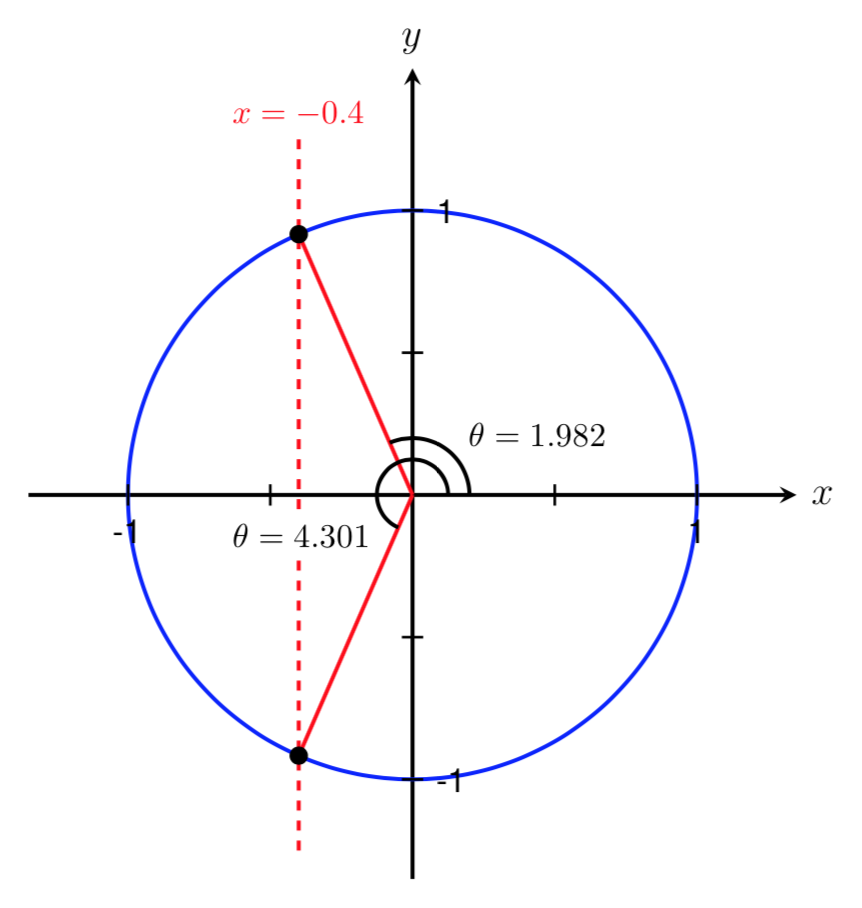
Find two angles in the interval \([0,2\pi]\) such that \(\cos(\theta)=-0.4\text{.}\)
Solution
Let's start by drawing a picture and labeling the known information and the angles we are trying to find.
Since we are given a cosine value, we know that we are looking for angles with an \(x\) coordinate of \(-0.4\) on the unit circle. Below is a sketch showing two angles that correspond to \(\cos(\theta) = -0.4\text{.}\) Recall back to Example45 that these two angles lie in Quadrant II and Quadrant III since our cosine value is negative.
Since \(x=-0.4\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse cosine function we get that
\begin{equation*}
\theta = \cos^{-1}(-0.4)
\end{equation*}
To evaluate this, we can use our calculator. Since the output of the inverse function is an angle, our calculator will give us an angle in degrees if it is in degree mode or an angle in radians if it is in radian mode.
Here, we need to decide whether to provide our answer in degrees or radians. Since we are given the interval \([0,2\pi]\text{,}\) which is radians, we will provide our answers in radians. Using our calculator in radian mode we get that
\begin{equation*}
\theta \approx 1.982 \text{ radians}
\end{equation*}
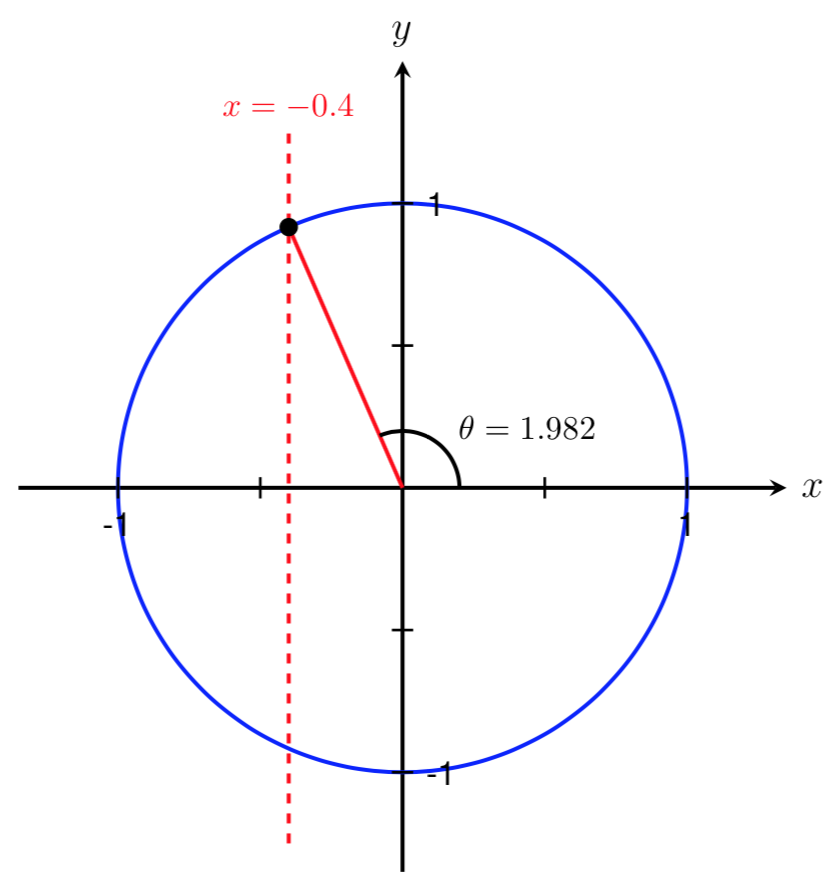
We have now found one angle in the interval \([0,2\pi]\) such that \(\cos(\theta) = -0.4\text{.}\) However, as shown above, \(\theta\) could lie in either Quadrant II or Quadrant III. Since 1.982 is bigger than \(\pi/2 \approx 1.571\) and smaller than \(\pi \approx 3.142\text{,}\) we know that \(\theta=1.982\) lies in Quadrant II. Therefore, we have found the angle shown below.
We can now use symmetry to find a second angle in the interval \([0,2\pi]\) such that \(\cos(\theta) = -0.4\text{.}\) From our work in Example45, we know this angle should be located in Quadrant III. By symmetry, we also know that the two angles shown below are equal.
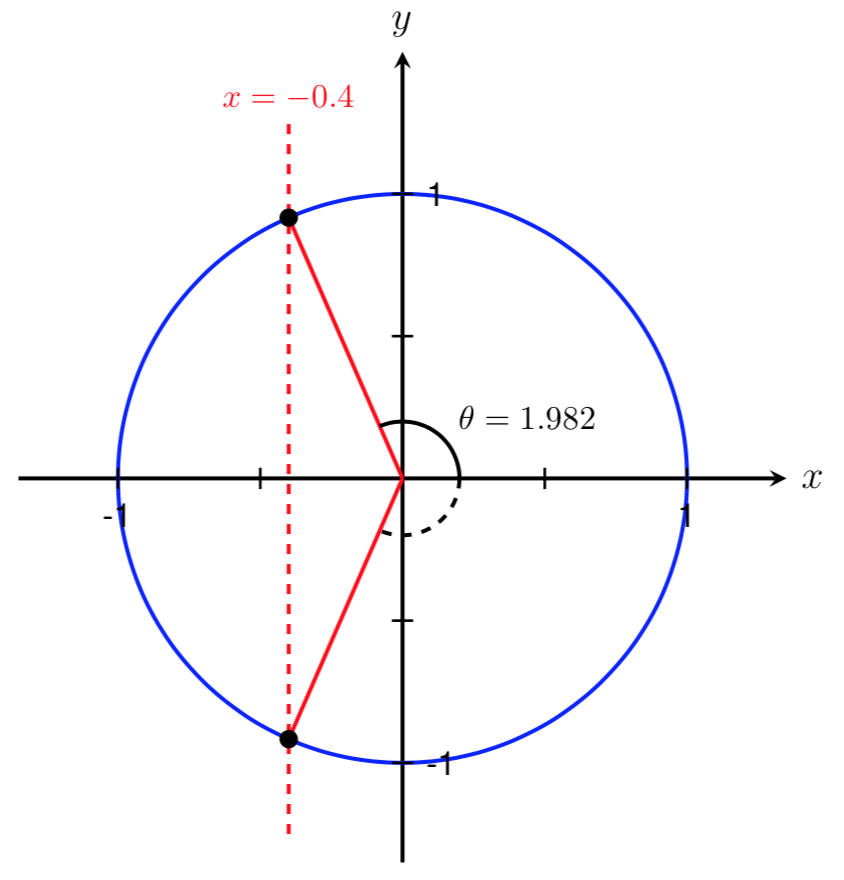
Therefore, to find the second angle, we can take the first angle we found and subtract it from \(2\pi\text{.}\) This gives us an angle of
\begin{equation*}
\theta \approx 2\pi - 1.982 \approx 4.301 \text{ radians}
\end{equation*}
Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\cos(\theta) = -0.4\) are
\begin{equation*}
\theta \approx 1.982 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 4.301 \text{ radians}
\end{equation*}
An easy way to check our solutions is to evaluate \(\cos(1.982)\) and \(\cos(4.301)\) on our calculators. If our calculator returns values close to \(-0.4\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get
\begin{equation*}
\cos(1.982)=-0.3997 \hspace{.25in} \text{ and } \hspace{.25in} \cos(4.301)=-0.3999
\end{equation*}
Since both of these values are very close and round to -0.4, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\cos(\theta)=-0.4\text{.}\)
Example53
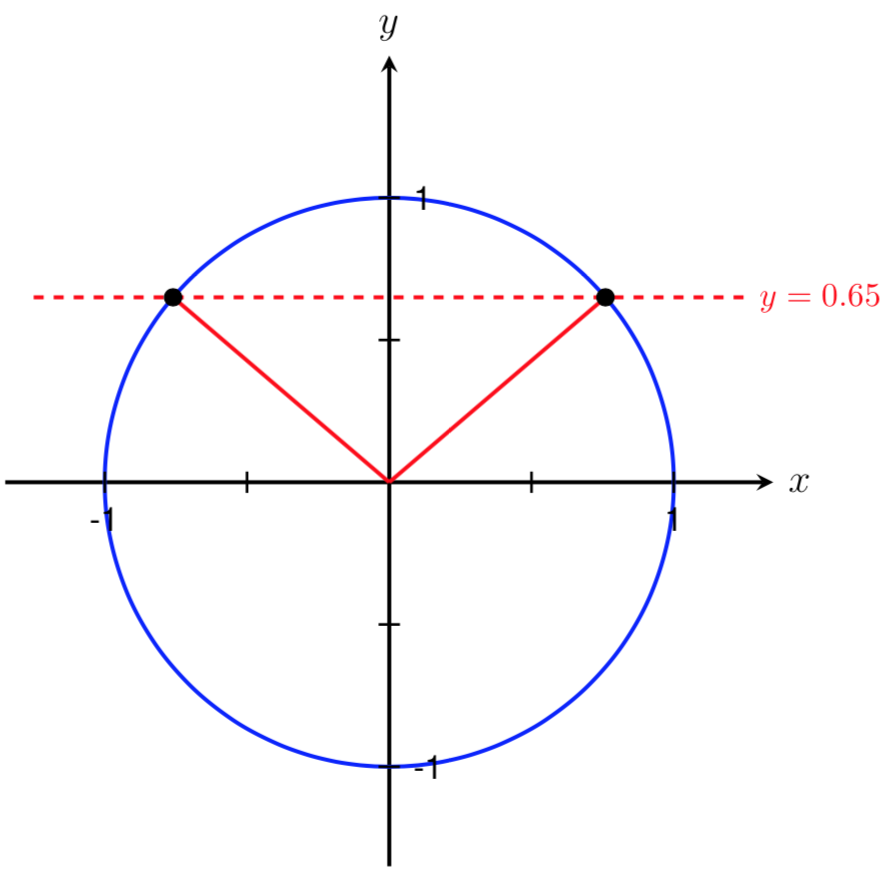
Find two angles in the interval \([0,2\pi]\) such that \(\sin(\theta)=0.65\text{.}\)
Solution
Let's start by drawing a picture and labeling the known information and the angles we are trying to find.
Since we are given a sine value, we know that we are looking for angles with an \(y\) coordinate of \(0.65\) on the unit circle. Below is a sketch showing two angles that correspond to \(\sin(\theta) = 0.65\text{.}\) Note that these two angles lie in Quadrant I and Quadrant II since our sine value is positive.
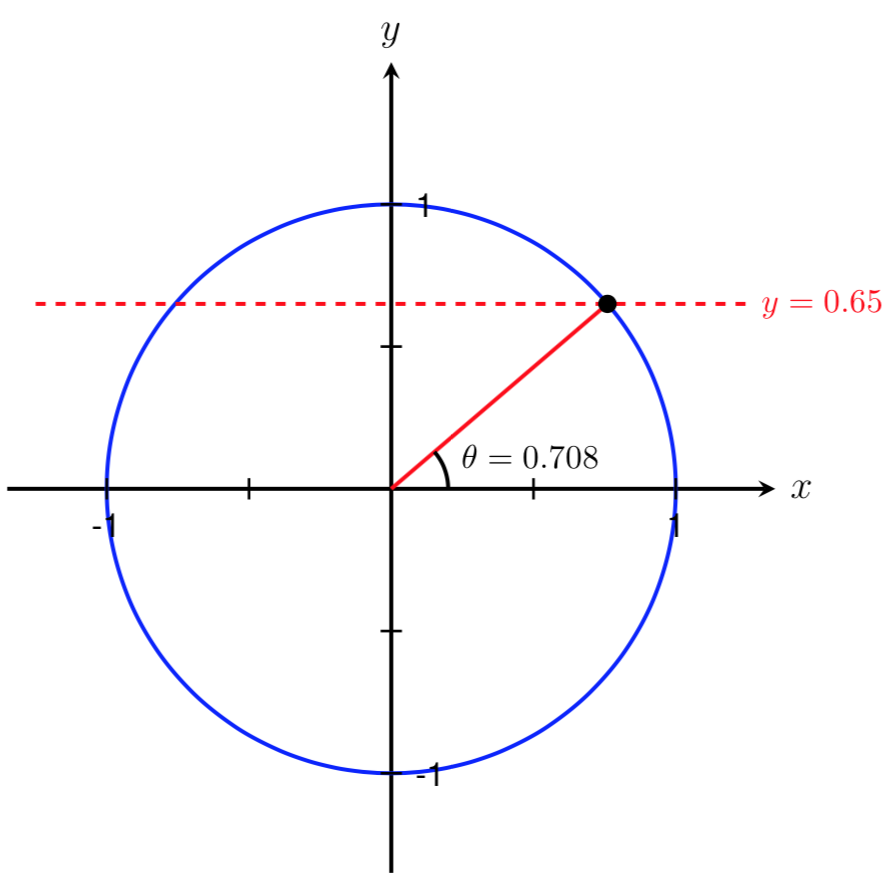
Since \(y=0.65\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse sine function we get that
\begin{equation*}
\theta = \sin^{-1}(0.65)
\end{equation*}
Using our calculator in radian mode we get that
\begin{equation*}
\theta \approx 0.708 \text{ radians}
\end{equation*}
We have now found one angle in the interval \([0,2\pi]\) such that \(\sin(\theta) = 0.65\text{.}\) However, as shown above, \(\theta\) could lie in either Quadrant I or Quadrant II. Since 0.708 is bigger than 0 and smaller than \(\pi/2 \approx 1.571\text{,}\) we know that \(\theta=0.708\) lies in Quadrant I. Therefore, we have found the angle shown below.
We can now use symmetry to find a second angle in the interval \([0,2\pi]\) such that \(\sin(\theta) = 0.65\text{.}\) From our work above, we know this angle should be located in Quadrant II. By symmetry, we also know that the two angles shown below are equal.
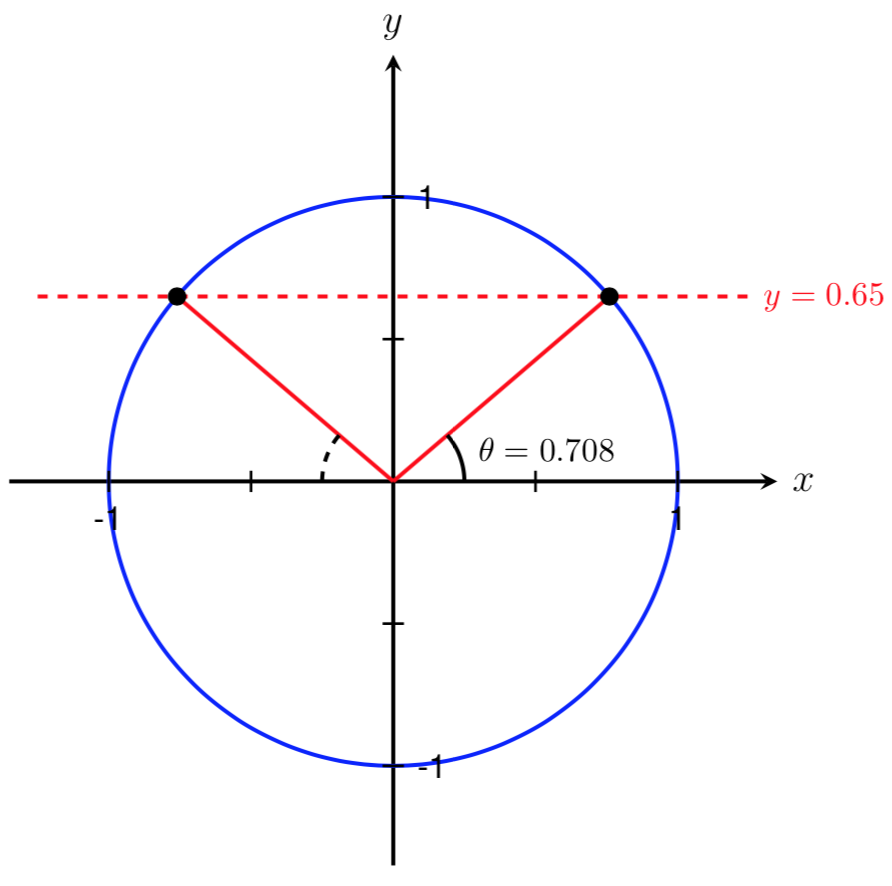
Therefore, to find the second angle, we can take the first angle we found and subtract it from \(\pi\text{.}\) This gives us an angle of
\begin{equation*}
\theta \approx \pi - 0.708 \approx 2.434 \text{ radians}
\end{equation*}
Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\sin(\theta) = 0.65\) are
\begin{equation*}
\theta \approx 0.708 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 2.434 \text{ radians}
\end{equation*}
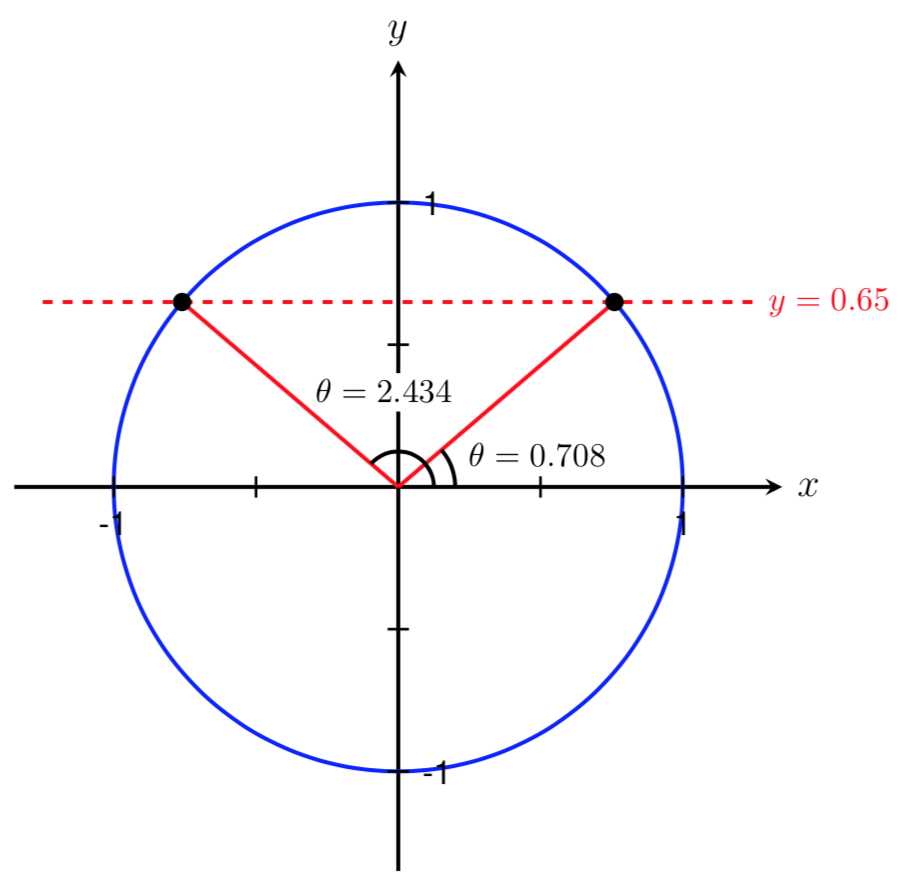
Before we move on, let's check our solutions by evaluating \(\sin(0.708)\) and \(\sin(2.434)\) on our calculators. If our calculator returns values close to \(0.65\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get
\begin{equation*}
\sin(0.708)=0.6503 \hspace{.25in} \text{ and } \hspace{.25in} \sin(2.434)=0.6500
\end{equation*}
Since both of these values are very close to 0.65, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\sin(\theta)=0.65\text{.}\)
Example54
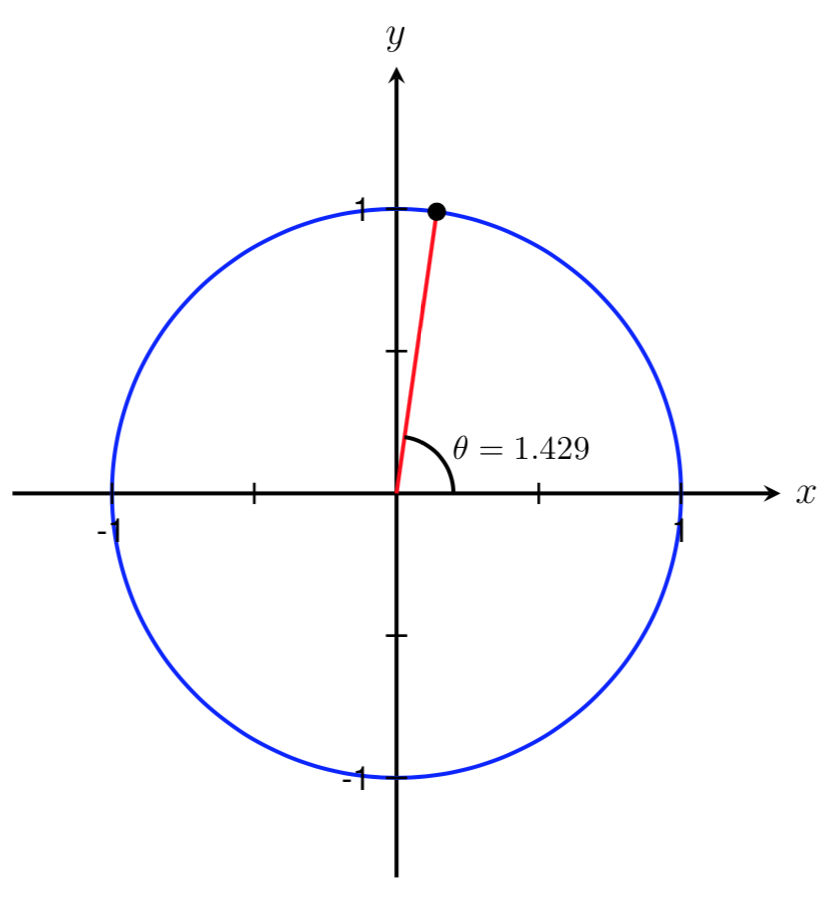
Find all angles in the interval \([0,2\pi]\) such that \(\tan(\theta)=7\text{.}\)
Solution
Since we are given a tangent value, we know that we are looking for angles where \(y/x=7\) on the unit circle. In addition, our tangent value is positive, so this means that \(\theta\) must lie in Quadrant I, where both \(x\) and \(y\) are positive, or in Quadrant III, where both \(x\) and \(y\) are negative.
Since \(\tan(\theta)=7\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse tangent function we get that
\begin{equation*}
\theta = \tan^{-1}(7)
\end{equation*}
Using our calculator in radian mode we get that
\begin{equation*}
\theta \approx 1.429 \text{ radians}
\end{equation*}
We have now found one angle in the interval \([0,2\pi]\) such that \(\tan(\theta) = 7\text{.}\) However, from our work above, we know that \(\theta\) could lie in either Quadrant I or Quadrant III. Since 1.429 is bigger than 0 and smaller than \(\pi/2 \approx 1.571\text{,}\) we know that \(\theta=1.429\) lies in Quadrant I. Therefore, we have found the angle shown below.
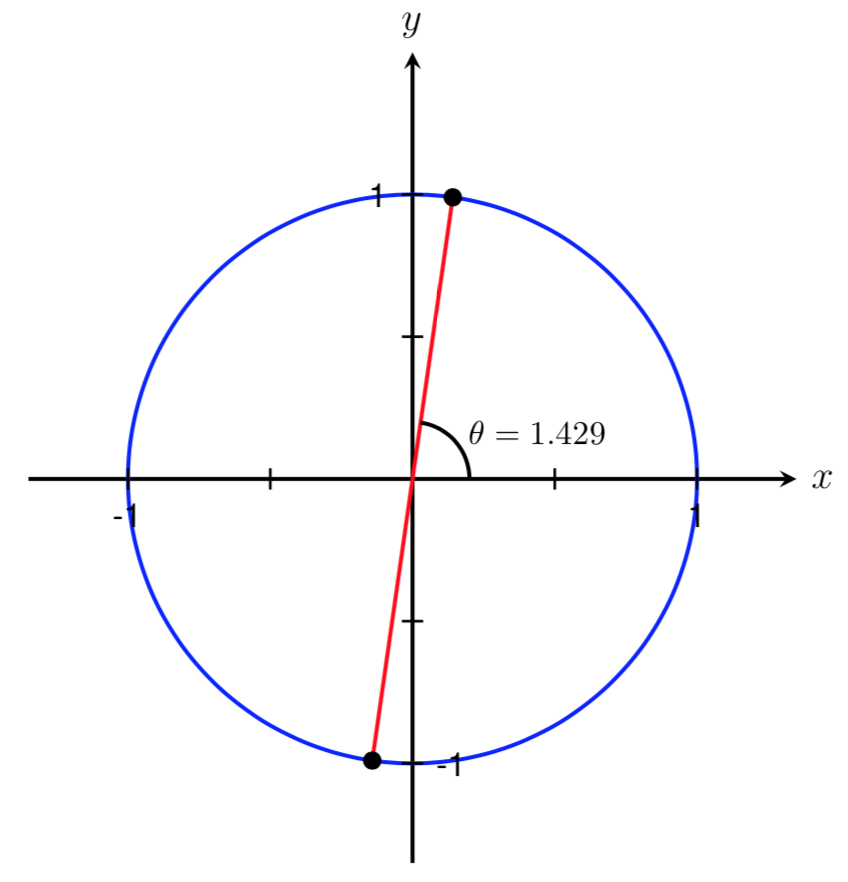
We can now use our knowledge of the tangent function to find a second angle in the interval \([0,2\pi]\) such that \(\tan(\theta) = 7\text{.}\) From our work above, we know this angle should be located in Quadrant III, and from Section, we know that the period of tangent is \(\pi\text{.}\) Therefore, the other angle where \(\tan(\theta)=7\) should be located halfway around the unit circle from our first value.
To find this second angle, we can add \(\pi\) to the first angle we found, which gives us an angle of
\begin{equation*}
\theta \approx 1.429 + \pi \approx 4.570 \text{ radians}
\end{equation*}
Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\tan(\theta) = 7\) are
\begin{equation*}
\theta \approx 1.429 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 4.570 \text{ radians}
\end{equation*}
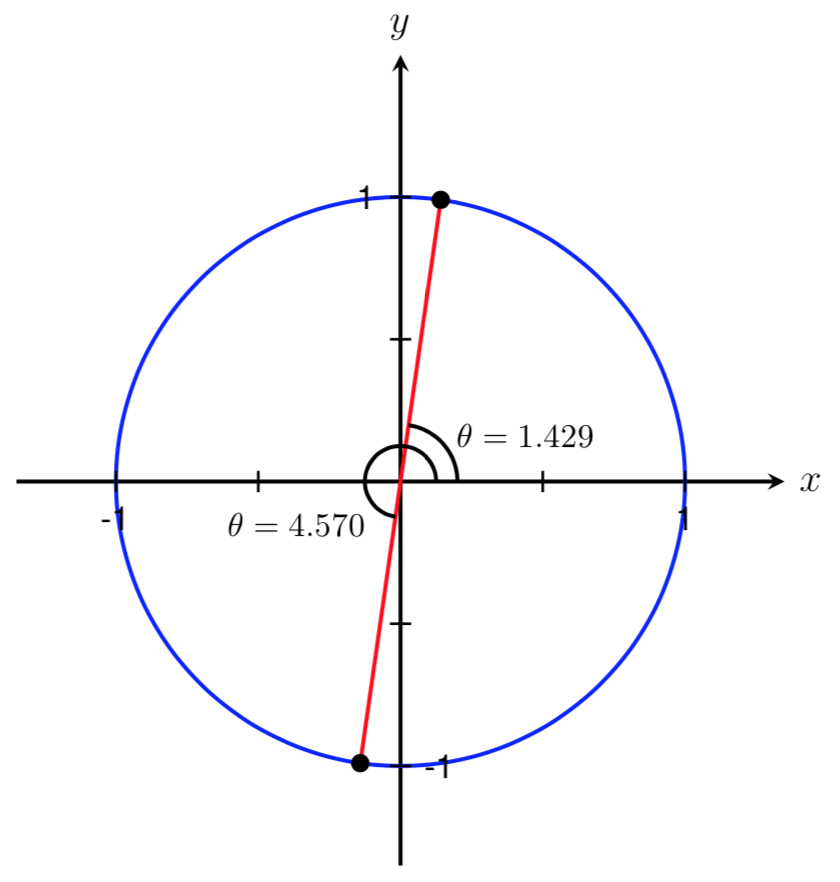
Before we move on, let's check our solutions by evaluating \(\tan(1.429)\) and \(\tan(4.570)\) on our calculators. If our calculator returns values close to \(7\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get
\begin{equation*}
\tan(1.429)=7.005 \hspace{.25in} \text{ and } \hspace{.25in} \tan(4.570)=6.975
\end{equation*}
Since both of these values are very close to 7, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\tan(\theta)=7\text{.}\)
Using inverse trig functions, we can also solve for the angles of a right triangle given two of its sides.
Example55
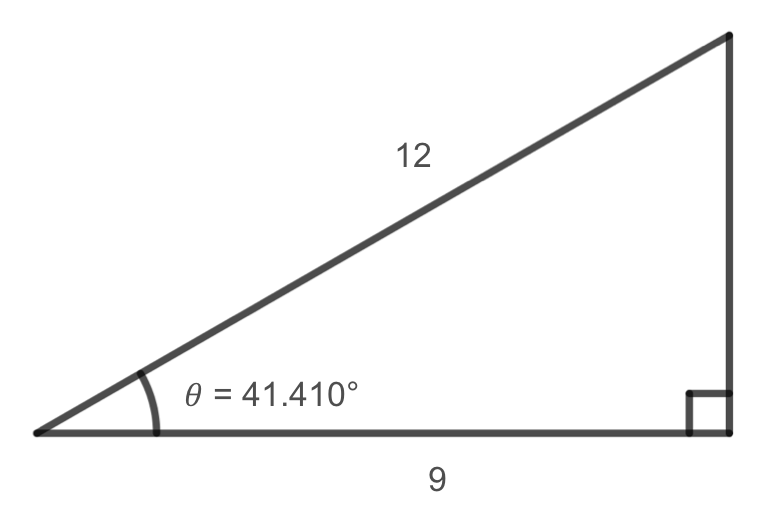
Solve the triangle for the angle \(\theta\text{.}\)
Solution
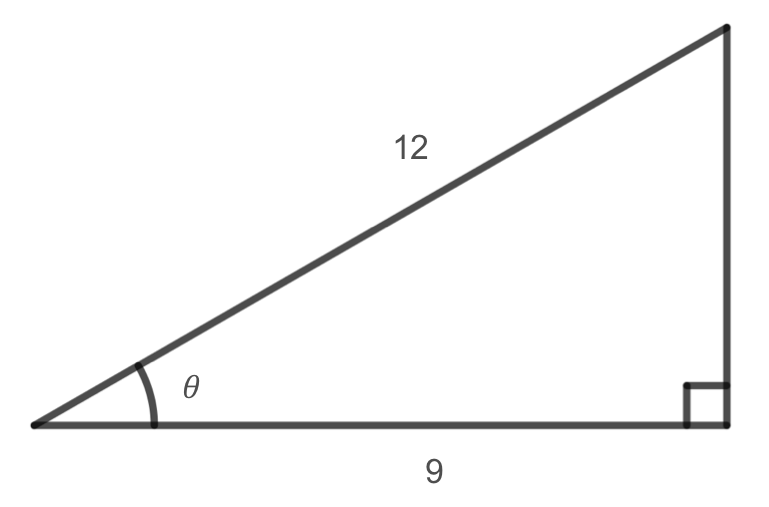
Since we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.
\begin{align*}
\cos(\theta) \amp = \frac{9}{12} \amp\amp\text{Using the definition of the inverse} \\
\\
\theta \amp = \cos^{-1}\left(\frac{9}{12}\right) \amp\amp\text{Evaluating on our calculator} \\
\\
\theta \amp \approx 0.723 \text{ radians} \amp\amp\text{or about } \ 41.410^\circ
\end{align*}