Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionThe Laws of Sines and Cosines
Although right triangles allow us to solve many applications, it is more common to find scenarios where the triangle we are interested in does not have a right angle.
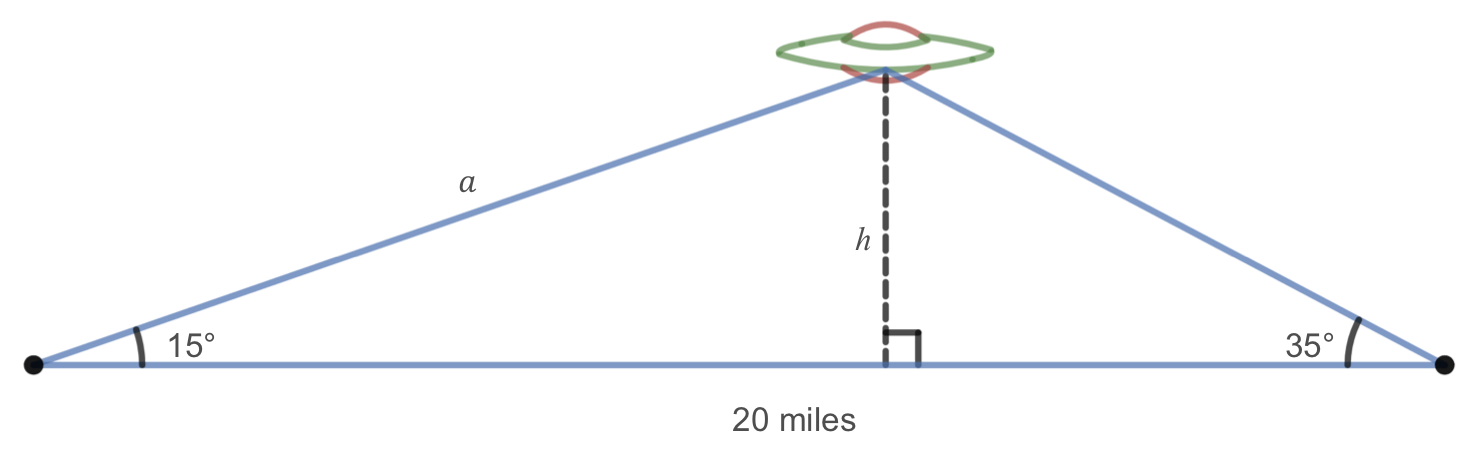
Two radar stations located 20 miles apart both detect a UFO located between them. The angle of elevation measured by the first station is 15 degrees. The angle of elevation measured by the second station is 35 degrees. What is the altitude of the UFO?
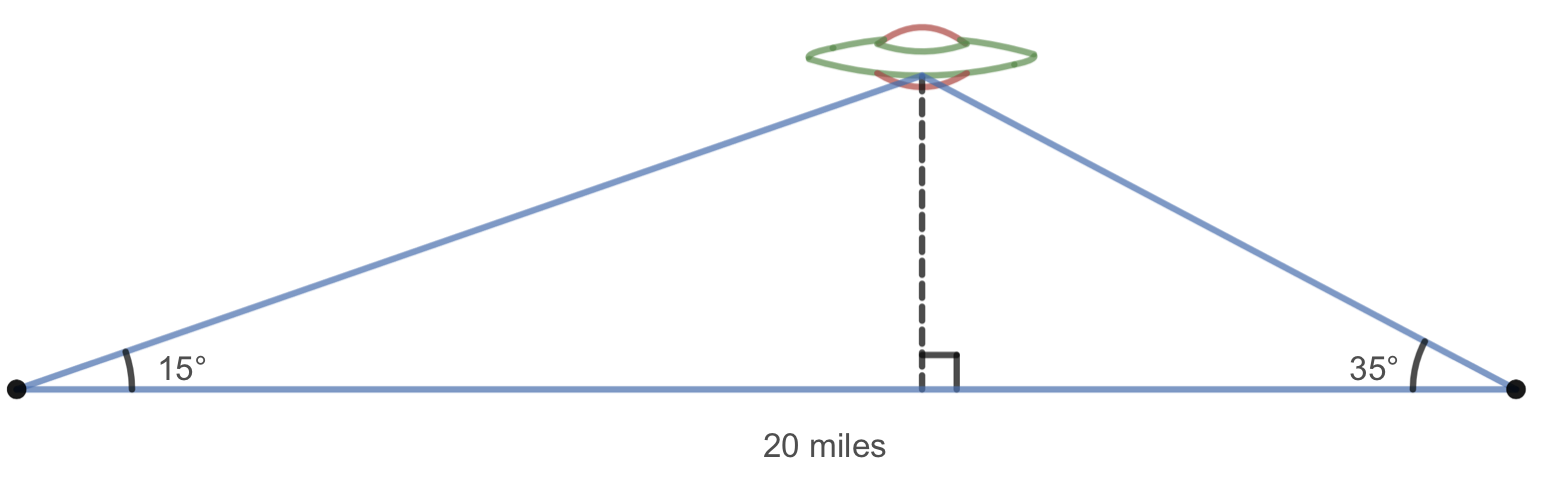
We see that the triangle formed by the UFO and the two stations is not a right triangle. Of course, in any triangle we could draw a perpendicular line from one vertex to the opposite side, forming two right triangles, but it would be nice to have methods for working directly with non-right triangles. In this section, we will expand upon right triangle trigonometry and adapt it to non-right triangles.
SubsectionStandard Triangle Labeling
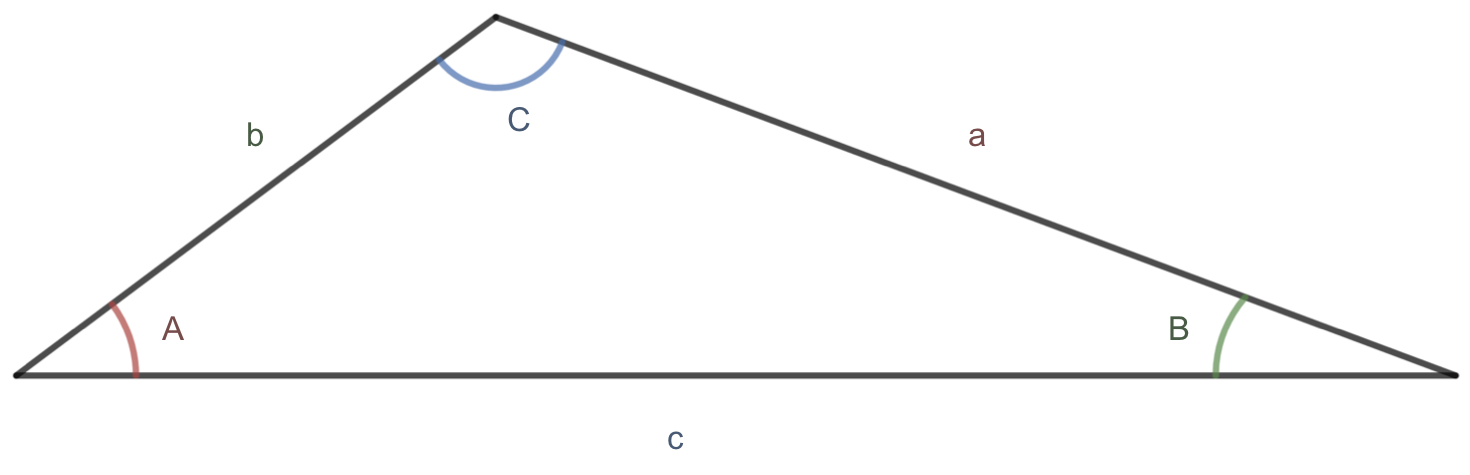
Before we begin solving non-right triangles, we must first decide on a standard way to label them. Below is a picture showing the standard triangle labeling that we will use in this section. The same letter pair gets assigned for each angle and its opposite side. Capital letters are used for angles, and lower case letters are used for the corresponding sides. It is crucial to use this convention when applying the Law of Sines and the Law of Cosines.
SubsectionLaw of Sines
We are going to now derive what is known as the Law of Sines. The Law of Sines establishes a relationship between pairs of angles and sides in triangles that are not necessarily right triangles. Given an arbitrary non-right triangle labeled in the standard way, we can draw a perpendicular line from one of the vertices to its opposite side, which we temporarily label \(h\text{,}\) to create two right triangles. We will use \(h\) to find a relationship between \(a\text{,}\) \(A\text{,}\) \(b\text{,}\) and \(B\text{.}\)
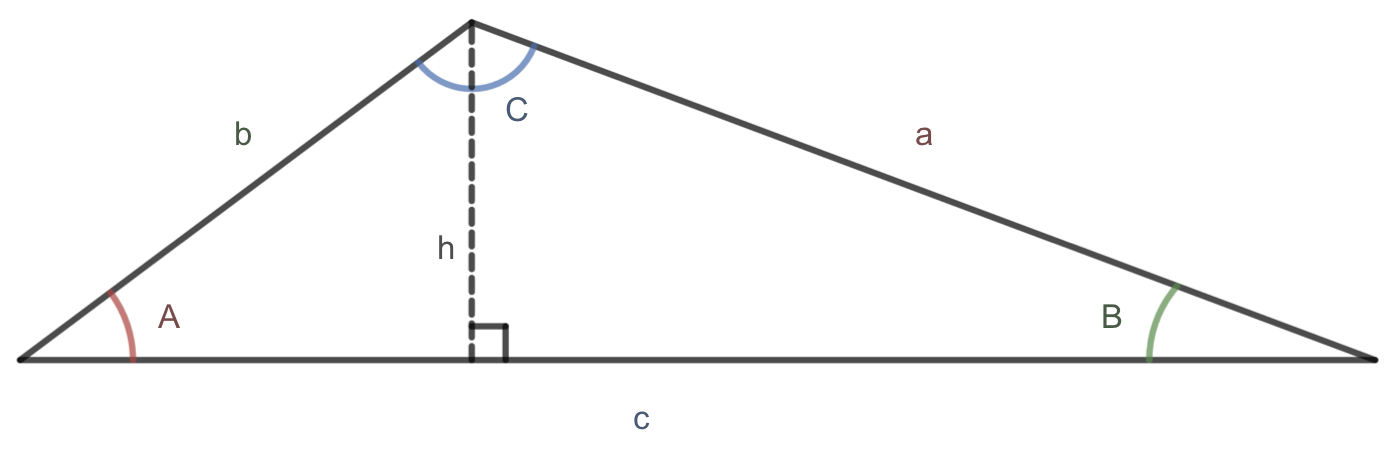
Using right triangle relationships, we have
\begin{equation*}
\sin(A)=\frac{h}{b} \hspace{.25in} \text{and} \hspace{.25in} \sin(B)=\frac{h}{a}\text{.}
\end{equation*}
Solving both equations for \(h\text{,}\) we get
\begin{equation*}
b\sin(A)=h \hspace{.25in} \text{and} \hspace{.25in} a\sin(B)=h
\end{equation*}
Since the \(h\) is the same in both equations, we establish
\begin{equation*}
b\sin(A)=a\sin(B)
\end{equation*}
Dividing both sides by \(ab\text{,}\) we conclude that
\begin{equation*}
\frac{\sin(A)}{a} = \frac{\sin(B)}{b}
\end{equation*}
Notice that we could have drawn \(h\) to be perpendicular to either \(a\) or \(b\) instead of \(c\text{.}\) If we'd drawn \(h\) perpendicular to a different side, we could similarly establish
\begin{equation*}
\frac{\sin(A)}{a} = \frac{\sin(C)}{c} \hspace{.25in} \text{and} \hspace{.25in} \frac{\sin(B)}{b} = \frac{\sin(C)}{c}
\end{equation*}
Collectively, these three relationships are called the Law of Sines.
Law of Sines
Given a triangle with angles and opposite sides labeled as shown,
\begin{equation*}
\frac{\sin(A)}{a} = \frac{\sin(B)}{b} = \frac{\sin(C)}{c}
\end{equation*}
For clarity, we call side \(a\) the corresponding side of angle \(A\text{.}\) Similarly, we call angle \(A\) the corresponding angle of side \(a\text{.}\)
We do likewise for side \(b\) and angle \(B\) and for side \(c\) and angle \(C\text{.}\)
When we use the Law of Sines, we can use any pair of ratios as an equation. In the most straightforward case, we know two angles and one of the corresponding sides.
Example91
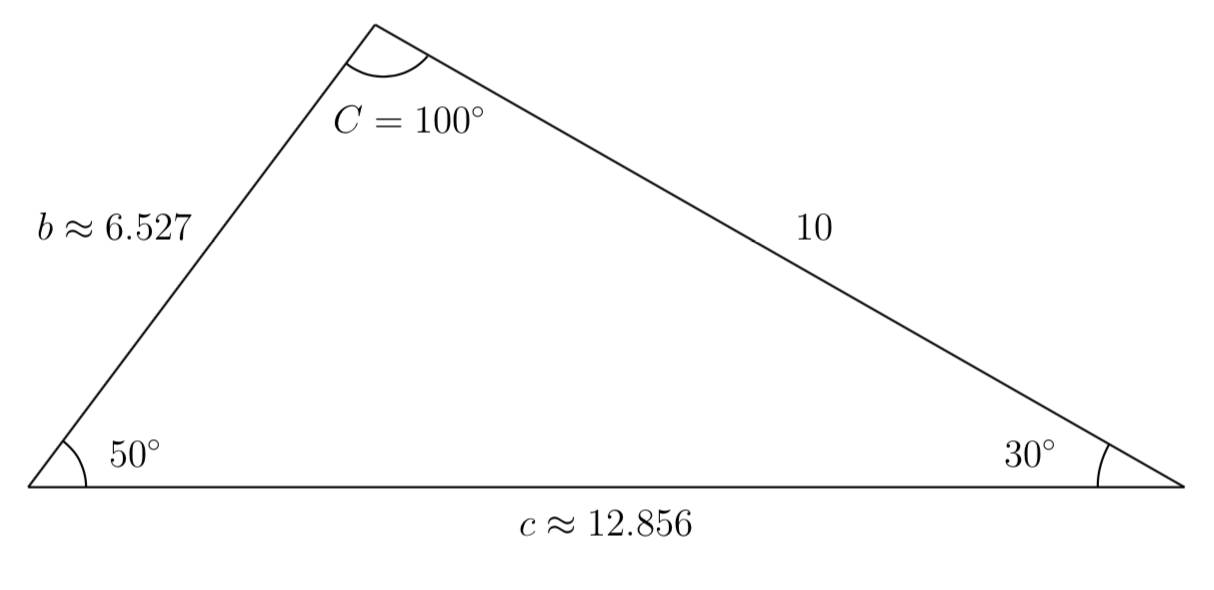
In the triangle shown below, solve for the unknown sides and angle.
Solution
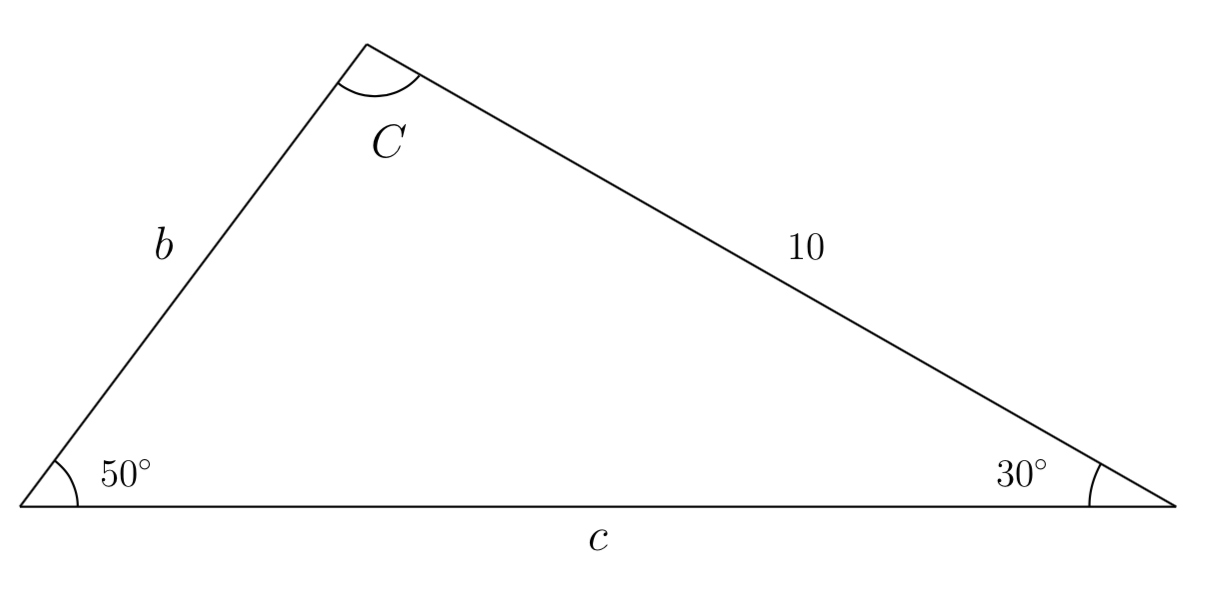
We solve for the unknown angle first. Since the three angles must add to 180 degrees, we can determine that
\begin{equation*}
\displaystyle C = 180^\circ - 50^\circ - 30^\circ = 100^\circ
\end{equation*}
To find an unknown side using the Law of Sines, we need to know the corresponding angle and another known ratio.
Since we know the angle \(50^\circ\) and its corresponding side, we can use \(\sin(50^\circ)/10\) as one of the two ratios. To solve for side \(b\text{,}\) we would use its corresponding angle, \(30^\circ\text{.}\) Using the Law of Sines we can set up the equation
\begin{equation*}
\frac{\sin(50^\circ)}{10} = \frac{\sin(30^\circ)}{b}
\end{equation*}
To solve for \(b\text{,}\) we can multiply both sides of the equation by \(b\) to get that
\begin{equation*}
b \cdot \frac{\sin(50^\circ)}{10} = \sin(30^\circ)
\end{equation*}
We can then multiply both sides by the reciprocal of \(\sin(50^\circ)/10\) to get \(b\) by itself. Therefore,
\begin{equation*}
b = \sin(30^\circ)\cdot\frac{10}{\sin(50^\circ)} \approx 6.527
\end{equation*}
Similarly, to solve for side \(c\text{,}\) we can use the Law of Sines to set up the equation
\begin{equation*}
\frac{\sin(50^\circ)}{10} = \frac{\sin(100^\circ)}{c}
\end{equation*}
Solving for \(c\text{,}\) we get that
\begin{equation*}
c = \sin(100^\circ)\cdot\frac{10}{\sin(50^\circ)} \approx 12.856
\end{equation*}
We have now solved for all of the unknown sides and angles of the triangle, as shown below.
Example92
Find the elevation of the UFO from the beginning of the section.
Solution
To find the elevation of the UFO, \(h\text{,}\) we can first find the distance from one radar station to the UFO, labeled as side \(a\) in the picture below and then use right triangle relationships to find the height of the UFO, \(h\text{.}\)
Since the angles in the triangle must add to \(180\) degrees, the unknown angle of the triangle shown below is \(C=180^\circ-15^\circ-35^\circ=130^\circ\text{.}\)
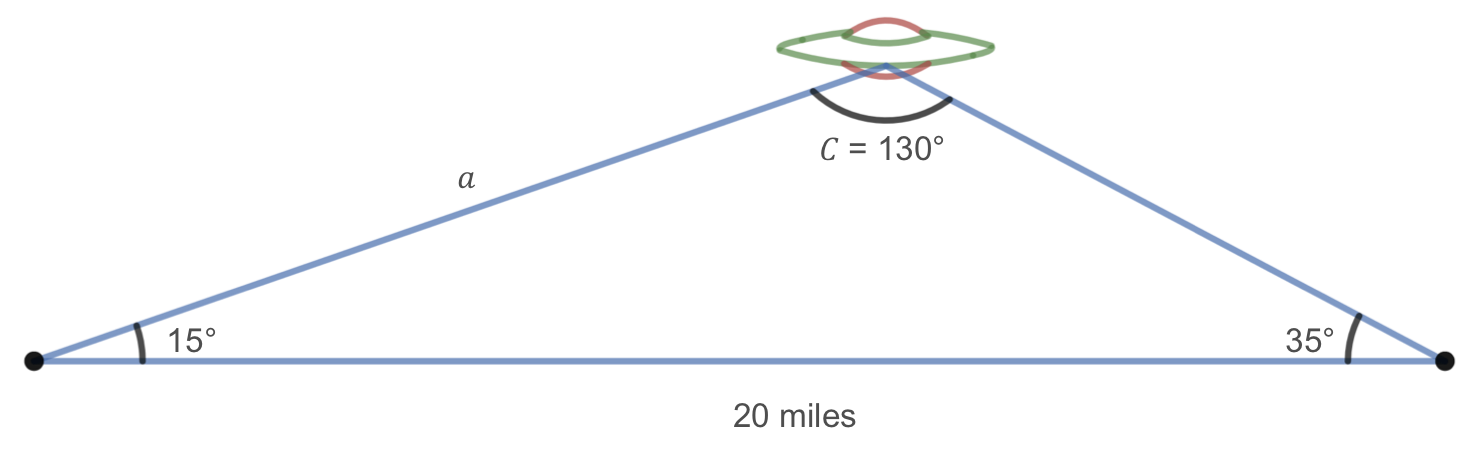
Since this angle is opposite the side of length 20, we can now use the Law of Sines to solve for side length \(a\) by setting up the equation
\begin{equation*}
\frac{\sin(130^\circ)}{20} = \frac{\sin(35^\circ)}{a}
\end{equation*}
Solving for \(a\text{,}\) we get that
\begin{equation*}
a = \frac{20\sin(35^\circ)}{\sin(35^\circ)} \approx 14.975 \text{ miles}
\end{equation*}
Therefore, the distance from one radar station to the UFO is about 15 miles.
Now that we know side length \(a\text{,}\) we can use right triangle relationships to solve for \(h\text{.}\)
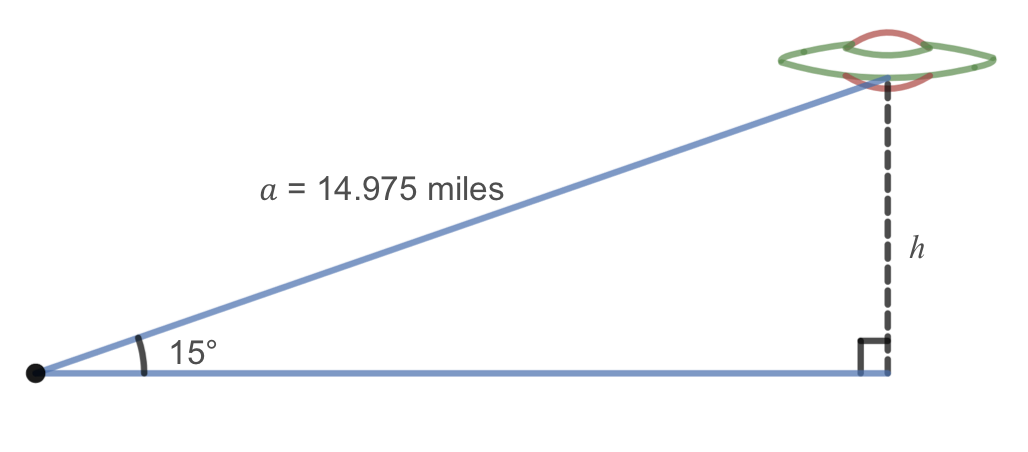
Using the sine function, we get that
\begin{equation*}
\sin(15^\circ) = \frac{\text{opp}}{\text{hyp}} = \frac{h}{a} = \frac{h}{14.975}
\end{equation*}
Solving for \(h\text{,}\) we get that
\begin{equation*}
h = 14.975\sin(15^\circ) \approx 3.876 \text{ miles}
\end{equation*}
Therefore, the altitude of the UFO is 3.876 miles.
In addition to solving triangles in which two angles are known, the Law of Sines can be used to solve for an angle when two sides and one corresponding angle are known.
Example93
In the triangle shown below, solve for the unknown sides and angles.
Solution
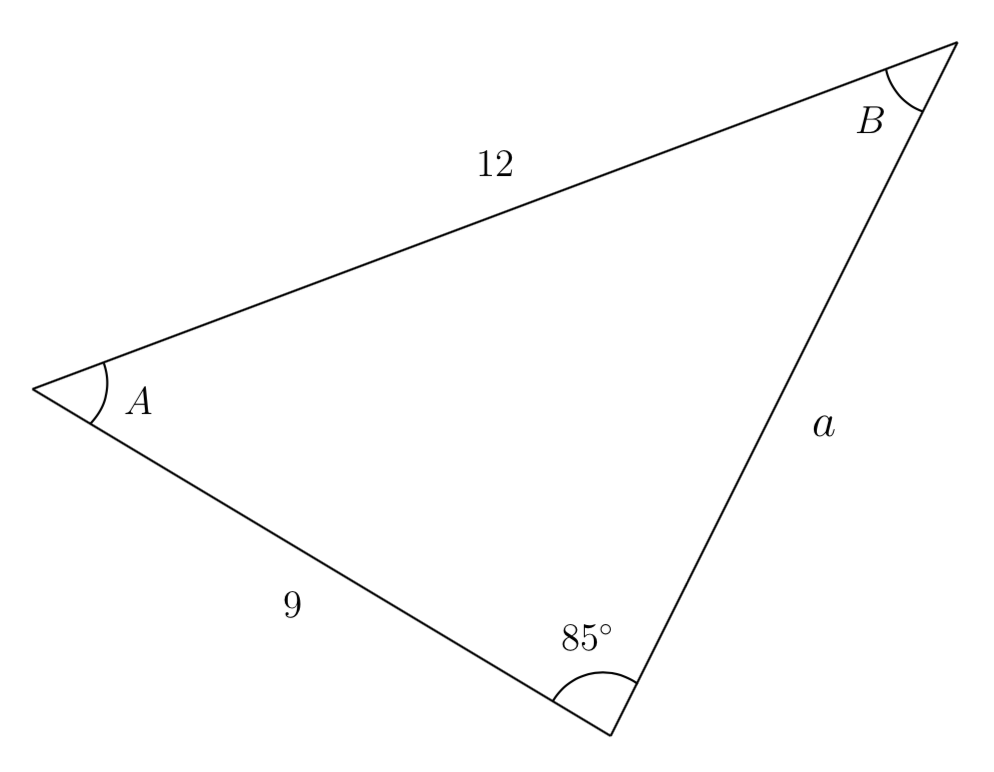
In choosing which pair of ratios from the Law of Sines to use, we always want to pick a pair where we know three of the four pieces of information in the equation.
In this case, we know the angle \(85^\circ\) and its corresponding side, so we will use the ratio \(\sin(85^\circ)/12\text{.}\) Since our only other known information is the side with length 9, we will use that side and solve for its corresponding angle. Using the Law of Sines, we get the equation
\begin{equation*}
\frac{\sin(85^\circ)}{12} = \frac{\sin(B)}{9}
\end{equation*}
To solve for \(B\text{,}\) we can multiply both sides of the equation by \(9\) to get that
\begin{equation*}
9 \cdot \frac{\sin(50^\circ)}{10} = \sin(B)
\end{equation*}
We can now use the inverse sine function to solve for \(B\text{.}\) Remember that when we use the inverse sine function, there are two possible answers. Using a calculator, we get that
\begin{equation*}
B = \sin^{-1}\left(\frac{9\sin(85^\circ)}{12}\right) \approx 48.344^\circ
\end{equation*}
To solve for the other possible solution, we can use symmetry to get that
\begin{equation*}
B \approx 180^\circ - 48.344^\circ = 131.656^\circ
\end{equation*}
If \(B \approx 131.656^\circ\text{,}\) then \(A \approx 180^\circ - 85^\circ - 131.656^\circ = -36.656^\circ\text{,}\) which does not make sense. Therefore, we can disregard this second possible solution and conclude that the only possible solution for this angle is
\begin{equation*}
B \approx 48.344^\circ
\end{equation*}
Now that we have two angles, we can solve for the third one. Since all of the angles must add up to \(180\) degrees, we have that
\begin{equation*}
A \approx 180^\circ - 85^\circ - 48.344^\circ = 46.656^\circ
\end{equation*}
Now that we know \(A\text{,}\) we can proceed as in earlier examples to find the unknown side \(a\text{.}\) Using the Law of Sines, we get that
\begin{equation*}
\frac{\sin(85^\circ)}{12} = \frac{\sin(46.656^\circ)}{a}
\end{equation*}
Solving for \(a\text{,}\) we get that
\begin{equation*}
a = \frac{12\sin(46.646^\circ)}{\sin(85^\circ)} \approx 8.760
\end{equation*}
We have now solved for all of the unknown sides and angles of the triangle, as shown below.
Caution94
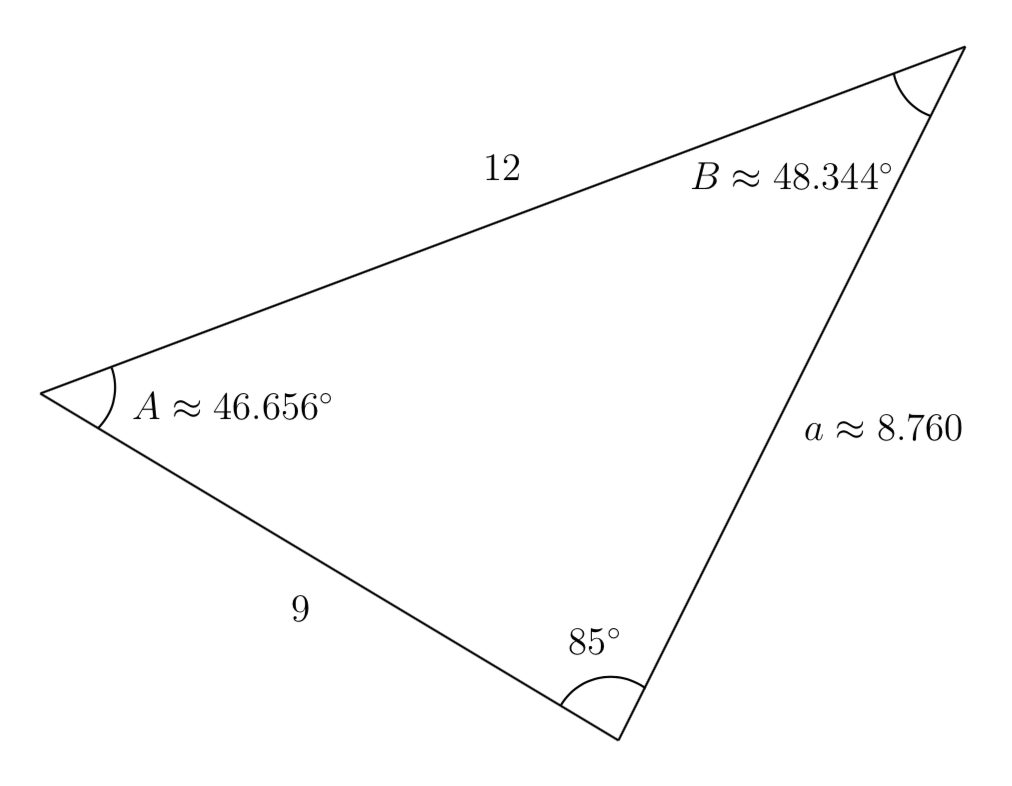
Notice that in the problem above, when we use the Law of Sines to solve for an unknown angle, there can be two possible solutions. This is called the ambiguous case and can arise when we know two sides and a non-included angle. In the ambiguous case we may find that a particular set of given information can lead to 2 solutions, 1 solution, or no solution at all. However, when an accurate picture of the triangle or suitable context is available, we can determine which angle is desired.
Example95
Given \(A=80^\circ\text{,}\) \(a=120\text{,}\) and \(b=121\text{,}\) find the corresponding and missing sides and angles. If there is more than one possible solution, show both.
Solution
Using the Law of Sines, we get the equation
Let us start by drawing a picture with the given information.
\begin{equation*}
\dfrac{\sin(80^\circ)}{120}=\dfrac{\sin(B)}{121}
\end{equation*}
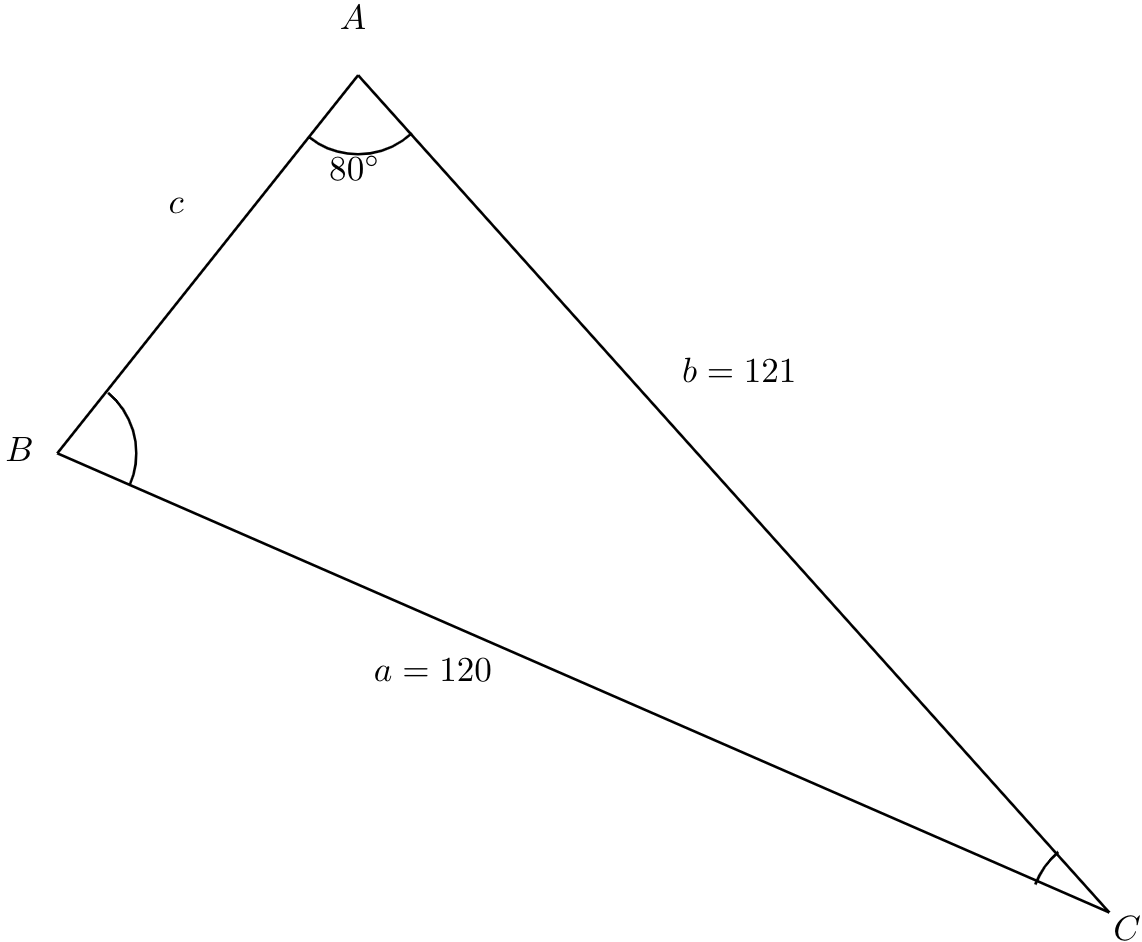
To solve for \(B\text{,}\) we can multiply both sides of the equation by \(121\) to get that
\begin{equation*}
121\cdot\dfrac{\sin(80^\circ)}{120}=\sin(B)
\end{equation*}
We can now use the inverse sine function to solve for \(B\text{.}\) Using our calculator, we get that
\begin{equation*}
B=\sin^{-1}\left(121\cdot\dfrac{\sin(80^\circ)}{120}\right)\approx83.224^\circ
\end{equation*}
To solve for the other possible solution, we can use symmetry to get that
\begin{equation*}
B\approx180^\circ-83.224^\circ=96.776^\circ
\end{equation*}
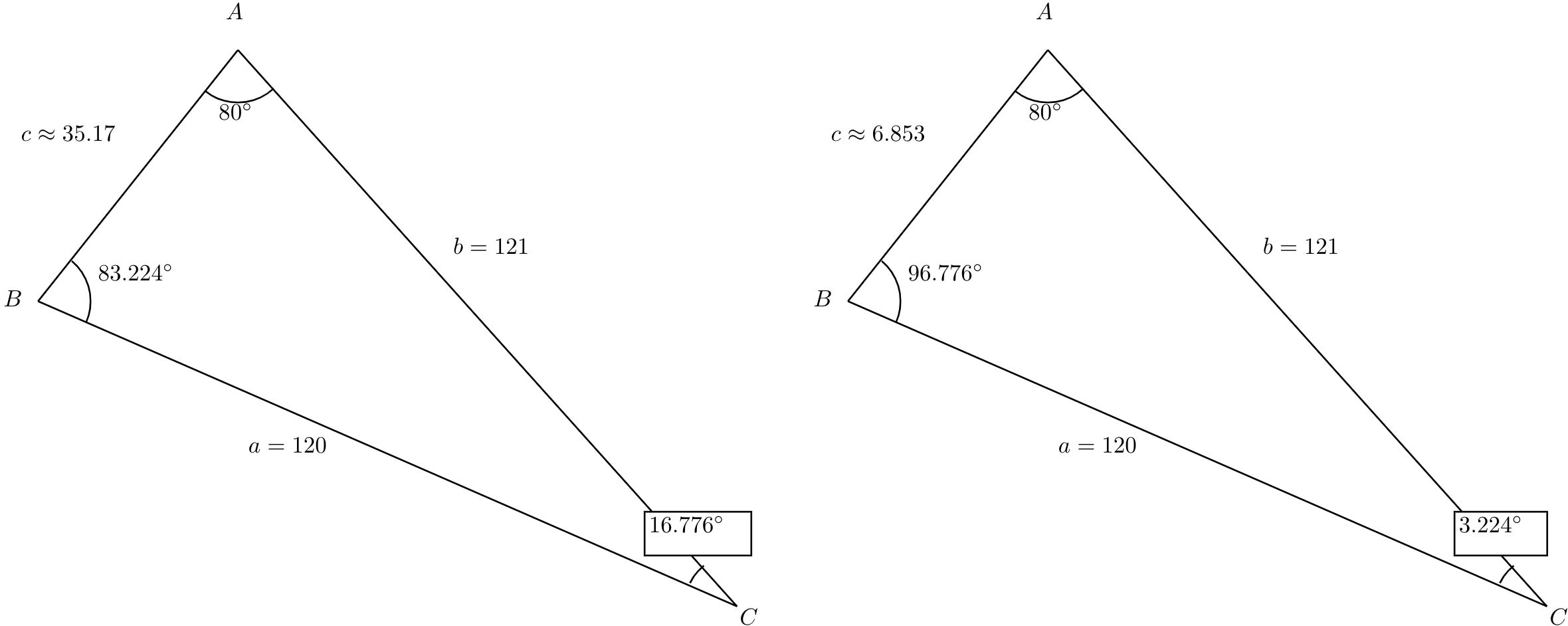
Since both of these answers make sense, we need to consider what happens for each of them. If \(B\approx83.224^\circ\text{,}\) then \(C\approx180^\circ-80^\circ-83.224^\circ\approx16.776^\circ\text{.}\) Now that we know \(C\text{,}\) we can again use the Law of Sines to find \(c\text{:}\)
\begin{equation*}
\dfrac{\sin(80^\circ)}{120}=\dfrac{\sin(16.776^\circ)}{c}
\end{equation*}
Solving for \(c\text{,}\) we get that
\begin{equation*}
c=\dfrac{120\sin(16.776^\circ)}{\sin(80^\circ)}\approx35.17
\end{equation*}
We have now solved for all of the unknowns for this value of \(B\text{.}\)
Now consider the case where \(B\approx96.776^\circ\text{.}\) If \(B\approx96.776^\circ\text{,}\) then \(C\approx180^\circ-80^\circ-96.776^\circ\approx3.224^\circ\text{.}\) Now that we know \(C\text{,}\) we can again use the Law of Sines to find \(c\text{:}\)
\begin{equation*}
\dfrac{\sin(80^\circ)}{120}=\dfrac{\sin(3.224^\circ)}{c}
\end{equation*}
Solving for \(c\text{,}\) we get that
\begin{equation*}
c=\dfrac{120\sin(3.224^\circ)}{\sin(80^\circ)}\approx6.853
\end{equation*}
We have now solved for all of the unknowns for this value of \(B\text{.}\) All together, we get that there are two possible triangles with \(a\text{,}\) \(A\text{,}\) and \(b\) as given:
SubsectionLaw of Cosines
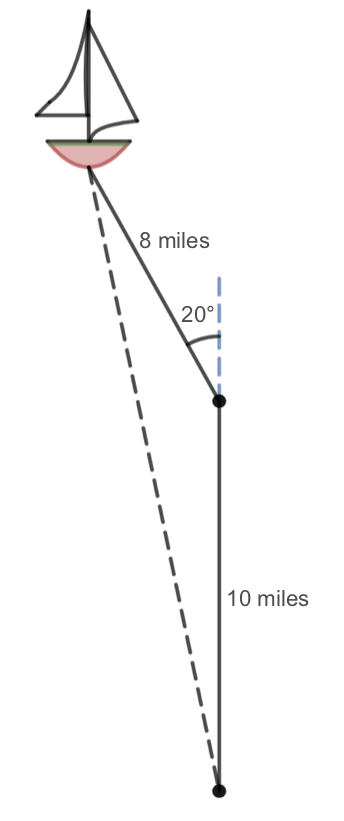
Suppose a boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles. How far from port is the boat?
Unfortunately, while the Law of Sines lets us address many non-right triangle cases, it does not allow us to address triangles where the one known angle is included between two known sides, which means it is not a corresponding angle for a known side. For this, we need another tool: the Law of Cosines.
Similar to the Law of Sines, the Law of Cosines establishes a relationship between the sides of a triangle and its angles. In particular, it relates all three sides and *any* of the three angles. We will derive it by again drawing adding in a perpendicular line and using what we know about right triangles.
Given an arbitrary non-right triangle, we can draw a perpendicular line from one vertex to the opposite side, which we temporarily label \(h\text{,}\) to create two right triangles. We will divide the base \(b\) into two pieces, one of which we will temporarily label \(x\text{.}\)
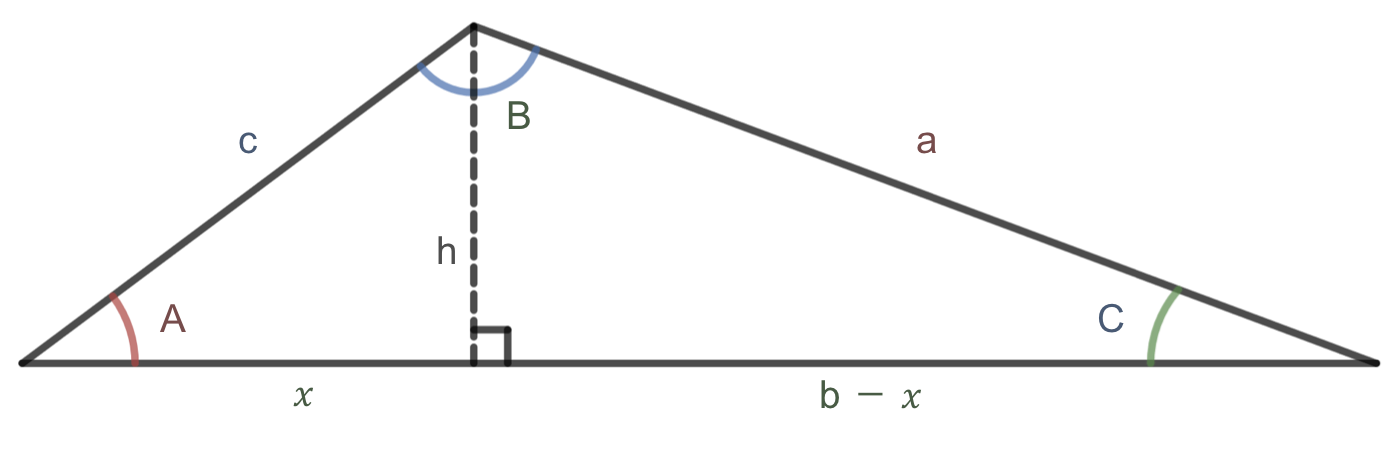
From this picture, we can establish the right triangle relationship
\begin{equation*}
\cos(A)=\frac{x}{c} \hspace{.25in} \text{or equivalently} \hspace{.25in} x=c\cos(A)
\end{equation*}
Using the Pythagorean Theorem, we can also establish that
\begin{equation*}
(b-x)^2+h^2=a^2 \hspace{.25in} \text{and} \hspace{.25in} x^2+h^2=c^2
\end{equation*}
Both of these equations can be solved for \(h^2\)
\begin{equation*}
h^2=a^2-(b-x)^2 \hspace{.25in} \text{and} \hspace{.25in} h^2=c^2-x^2
\end{equation*}
Since the left side of each equation is \(h^2\text{,}\) the right sides must be equal
\begin{align*}
c^2-x^2 \amp= a^2-(b-x)^2 \amp\amp \text{Multiplying out the right}\\
\\
c^2-x^2 \amp= a^2-(b^2-2bx+x^2) \amp\amp \text{Simplifying}\\
\\
c^2-x^2 \amp= a^2-b^2+2bx-x^2 \amp\amp \text{Simplifying}\\
\\
c^2 \amp= a^2-b^2+2bx \amp\amp \text{Isolating } a^2\\
\\
a^2 \amp= b^2+c^2-2bx \amp\amp \text{Substituting in } x=c\cos(A) \text{ from above}\\
\\
a^2 \amp= b^2+c^2-2bc\cos(A) \amp\amp
\end{align*}
This result is called the Law of Cosines. If we draw the line perpendicular to one of the other two sides, we could establish this relationship using any angle. The important thing to note is that the right side of the equation involves an angle and the sides adjacent to that angle while the left side of the equation involves the side opposite that angle.
Law of Cosines
Given a triangle with angles and opposite sides labeled as shown,
\begin{equation*}
a^2=b^2+c^2-2bc\cos(A)
\end{equation*}
\begin{equation*}
b^2=a^2+c^2-2ac\cos(B)
\end{equation*}
\begin{equation*}
c^2=a^2+b^2-2ab\cos(C)
\end{equation*}
Notice that if one of the angles of the triangle is 90 degrees, then the formula \(c^2=a^2+b^2-2ab\cos(C)\) simplifies to \(c^2=a^2+b^2\) since \(\cos(90^\circ)=0\text{.}\)
You should recognize this as the Pythagorean Theorem. Indeed, the Law of Cosines is sometimes called the Generalized Pythagorean Theorem since it extends the Pythagorean Theorem to non-right triangles.
In addition to solving for the missing side opposite one known angle, the Law of Cosines allows us to find the angles of a triangle when we know all three sides.
Example96
Given \(A=25^\circ\text{,}\) \(b=10\text{,}\) and \(c=20\text{,}\) find the missing side and angles.
Solution
Let's first draw a triangle with all the given information.
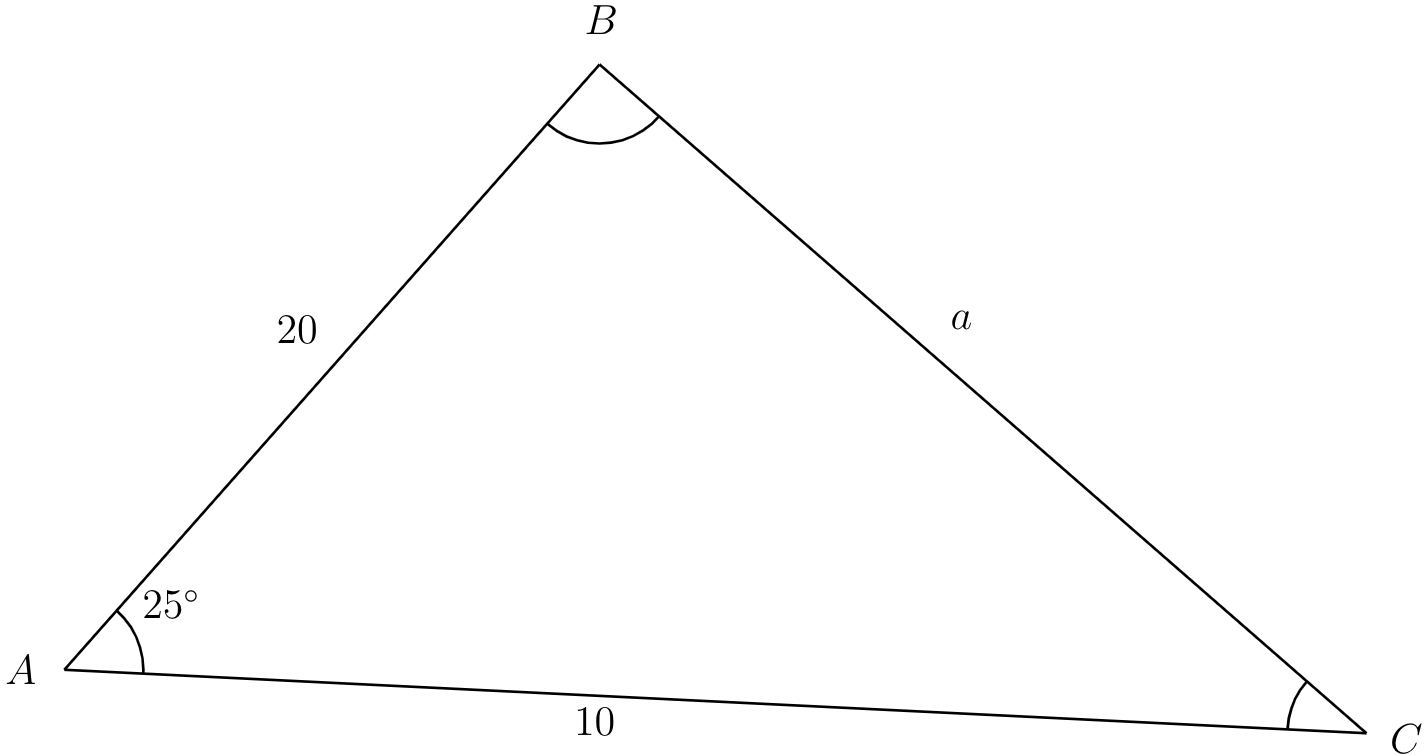
Since we are missing only one side length and it is opposite a known angle, we will use the Law of Cosines to find \(a\text{.}\) The Law of Cosines say that
\begin{equation*}
\begin{aligned}
a^2 \amp= b^2+c^2-2bc\cos(A) \\
a^2 \amp= 10^2+20^2-2(10)(20)\cos(25^\circ) \\
a^2 \amp\approx 136.477 \\
a \amp\approx 11.725
\end{aligned}
\end{equation*}
At this point we could use the Law of Sines or the Law of Cosines to find another angle, but we'll use the Law of Cosines. To find \(B\text{,}\) we have
\begin{equation*}
\begin{aligned}
b^2 \amp= a^2+c^2-2ac\cos(B) \\
10^2 \amp\approx 11.725^2+20^2-2(11.725)(20)\cos(B) \\
100 \amp\approx 537.476-469\cos(B) \\
-437.476 \amp\approx -469\cos(B) \\
cos(B)\amp\approx 0.933
\end{aligned}
\end{equation*}
Using the inverse cosine function, we get that \(B\approx 21.13^\circ\text{.}\) Finally, to find \(C\) we use the fact that there are \(180^\circ\) in a triangle:
\begin{equation*}
C\approx180^\circ-25^\circ-21.13^\circ\approx133.87^\circ\text{.}
\end{equation*}
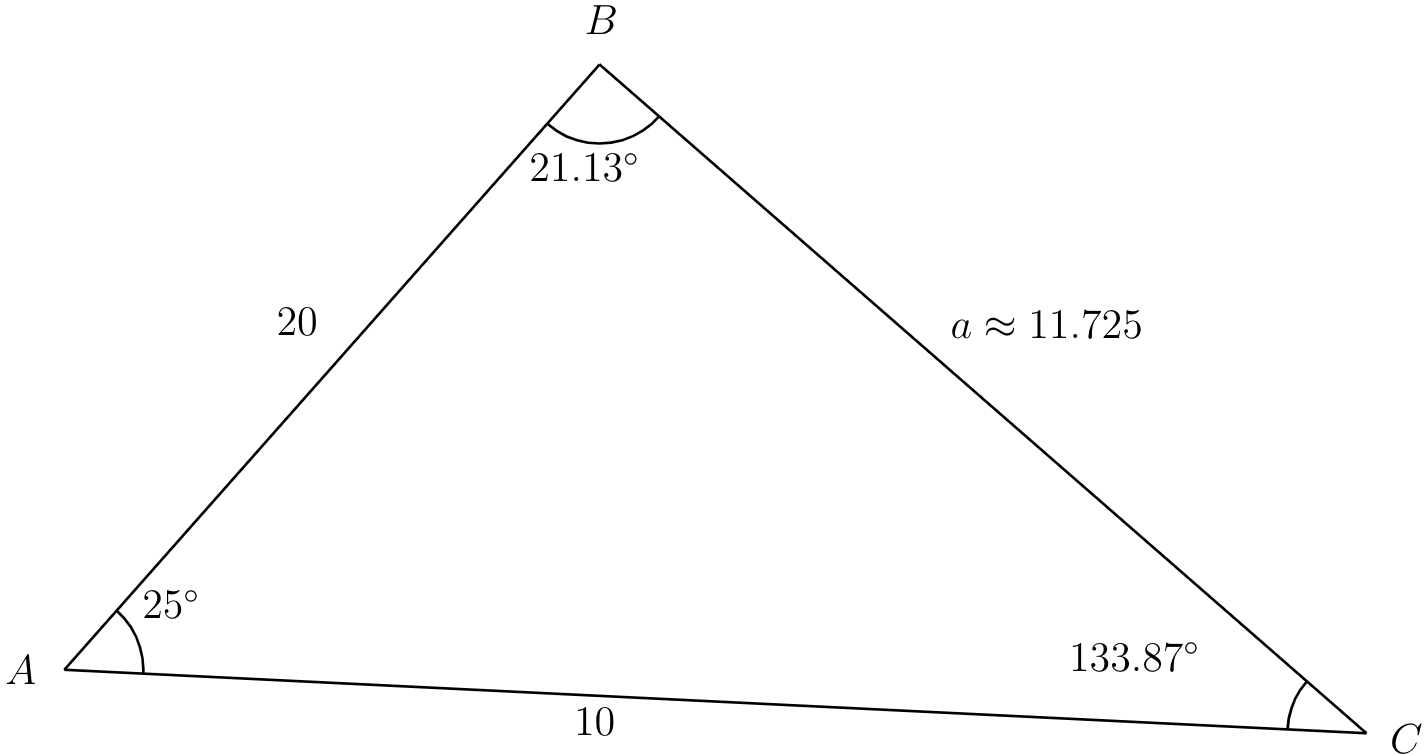
Notice that since the inverse cosine can return any angle between 0 and 180 degrees, there will not be any ambiguous cases when using the Law of Cosines to find an angle.