Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionRelationships Between Trigonometric Functions
So far, we have defined the sine, cosine, and tangent functions. There are three more trigonometric functions, which we define in this section. We will also explore relationships between the six trigonometric functions.
SubsectionReciprocal Trigonometric Functions
There are times when it can be useful to consider functions like \(1/\sin(\theta)\) or \(1/\cos(\theta)\text{.}\) This happens often enough that mathematicians have created special names for these types of functions. Generally, these functions are called reciprocal trigonometric functions, and they can be defined in terms of the sine, cosine, and tangent functions.
Reciprocal Trigonometric Functions
Given an angle \(\theta\text{,}\) we define:
\begin{align*}
\amp \text{the secant function as } \amp\amp \sec(\theta)=\frac{1}{\cos(\theta)}\\
\\
\amp \text{the cosecant function as } \amp\amp \csc(\theta)=\frac{1}{\sin(\theta)}\\
\\
\amp \text{the cotangent function as } \amp\amp \cot(\theta)=\frac{1}{\tan(\theta)}
\end{align*}
Example39
Find \(\sec\left(\frac{5\pi}{6}\right)\text{,}\) \(\csc\left(\frac{5\pi}{6}\right)\text{,}\) and \(\cot\left(\frac{5\pi}{6}\right)\text{.}\)
Solution
Since \(\frac{5\pi}{6}\) is a common angle on the unit circle, we have that
\begin{align*}
\sec\left(\frac{5\pi}{6}\right)\amp=\frac{1}{\cos\left(\frac{5\pi}{6}\right)} = \frac{1}{-\frac{\sqrt{3}}{2}} = -\frac{2}{\sqrt{3}} = -\frac{2\sqrt{3}}{3}\\
\\
\csc\left(\frac{5\pi}{6}\right)\amp=\frac{1}{\sin\left(\frac{5\pi}{6}\right)} = \frac{1}{\frac{1}{2}} = 2\\
\\
\cot\left(\frac{5\pi}{6}\right)\amp=\frac{1}{\tan\left(\frac{5\pi}{6}\right)} = \frac{1}{-\frac{1}{\sqrt{3}}} = -\sqrt{3}
\end{align*}
Example40
Using the triangle shown, evaluate \(\sec(\theta)\text{,}\) \(\csc(\theta)\text{,}\) and \(\cot(\theta)\text{.}\)
Solution
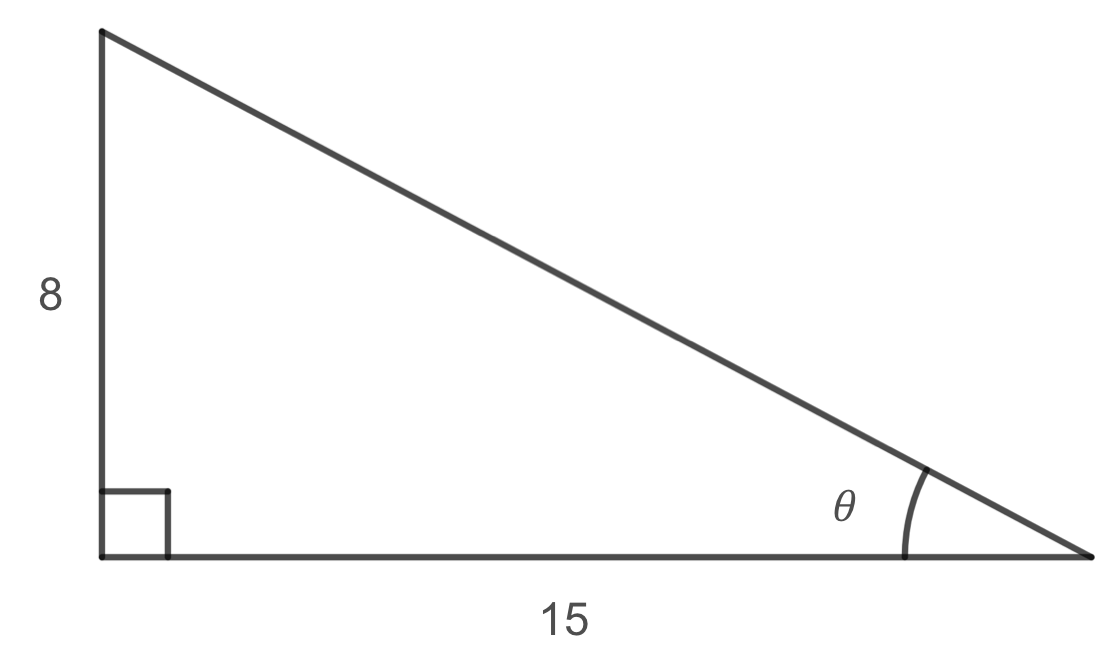
To find values for reciprocal trigonometric functions, we must first find values for \(\cos(\theta)\text{,}\) \(\sin(\theta)\text{,}\) and \(\tan(\theta)\text{.}\) We must also find the length of the hypotenuse. Letting the variable \(c\) represent the length of the hypotenuse and using the Pythagorean Theorem, we get that
\begin{align*}
c^2 \amp= 8^2 + 15^2 \\
c^2 \amp= 64 + 225 \\
c^2 \amp= 289 \\
c \amp= \pm \sqrt{289} \\
c \amp= 17
\end{align*}
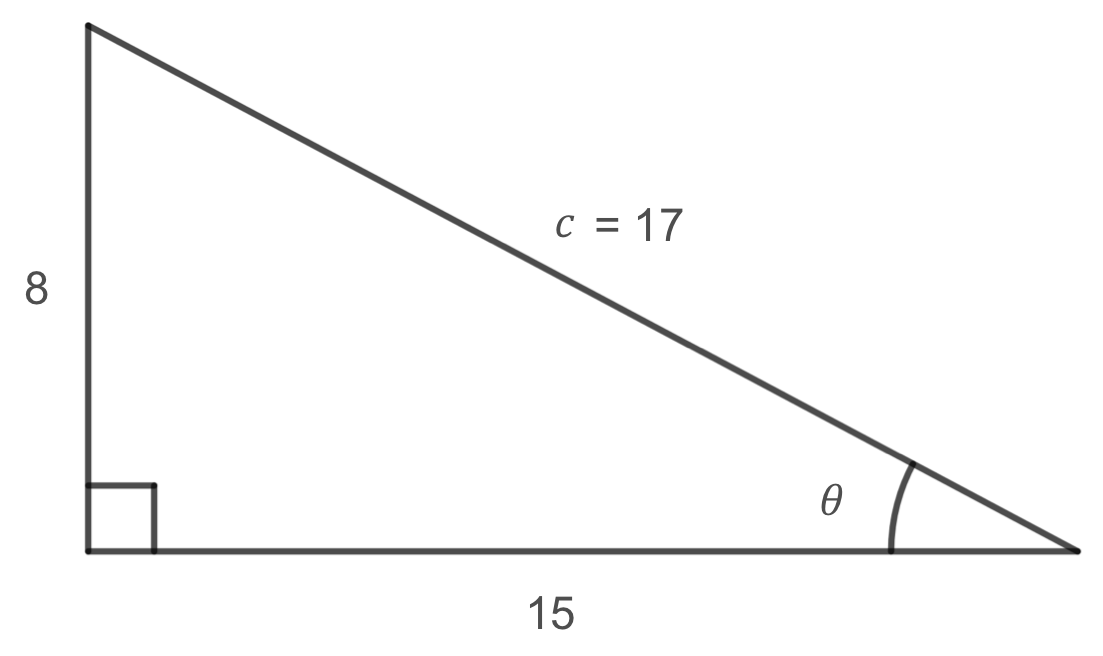
Now solving for \(\cos(\theta)\text{,}\) \(\sin(\theta)\text{,}\) and \(\tan(\theta)\text{,}\) we get that
\begin{align*}
\cos(\theta) \amp= \frac{15}{17} \\
\\
\sin(\theta) \amp= \frac{8}{17} \\
\\
\tan(\theta) \amp= \frac{8}{15}
\end{align*}
Finally, solving for the reciprocal trigonometric functions, we get
\begin{align*}
\sec(\theta) \amp= \frac{1}{\cos(\theta)} = \frac{17}{15} \\
\\
\csc(\theta) \amp= \frac{1}{\sin(\theta)} = \frac{17}{8} \\
\\
\cot(\theta) \amp= \frac{1}{\tan(\theta)} = \frac{15}{8}
\end{align*}
SubsectionCofunctions
Trigonometric functions are related to each other in special ways. In the last part of this section, we explored how sine, cosine, and tangent are related to the reciprocal trig functions cosecant, secant, and cotangent. We now return to Example30 from the previous Section to illustrate a special relationship between sine and cosine.
Example41
Using the triangle shown below, find \(\cos(\alpha)\text{,}\) \(\sin(\alpha)\text{,}\) \(\cos(\beta)\text{,}\) and \(\sin(\beta)\text{.}\)
Solution
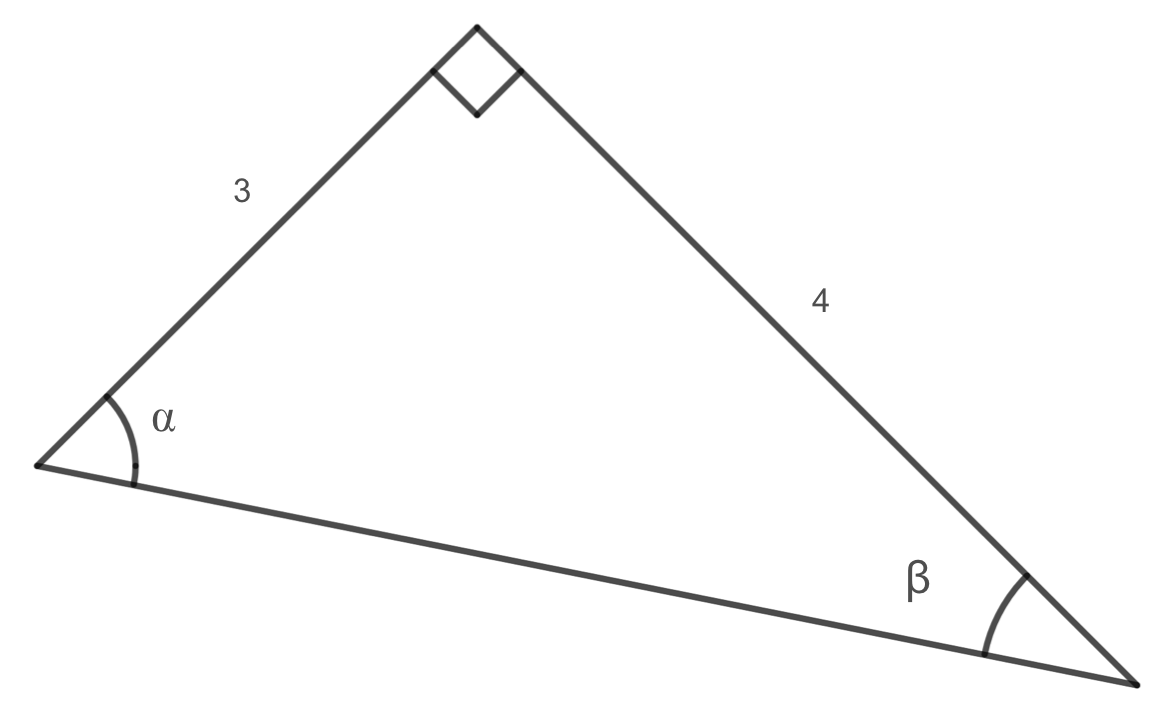
Before solving for the cosine and sine values of \(\alpha\) and \(\beta\text{,}\) we must first find the length of the hypotenuse. Using the Pythagorean theorem, we get that
\begin{align*}
c^2 \amp= 3^2 + 4^2 \\
c^2 \amp= 9 + 16 \\
c^2 \amp= 25 \\
c \amp = 5
\end{align*}
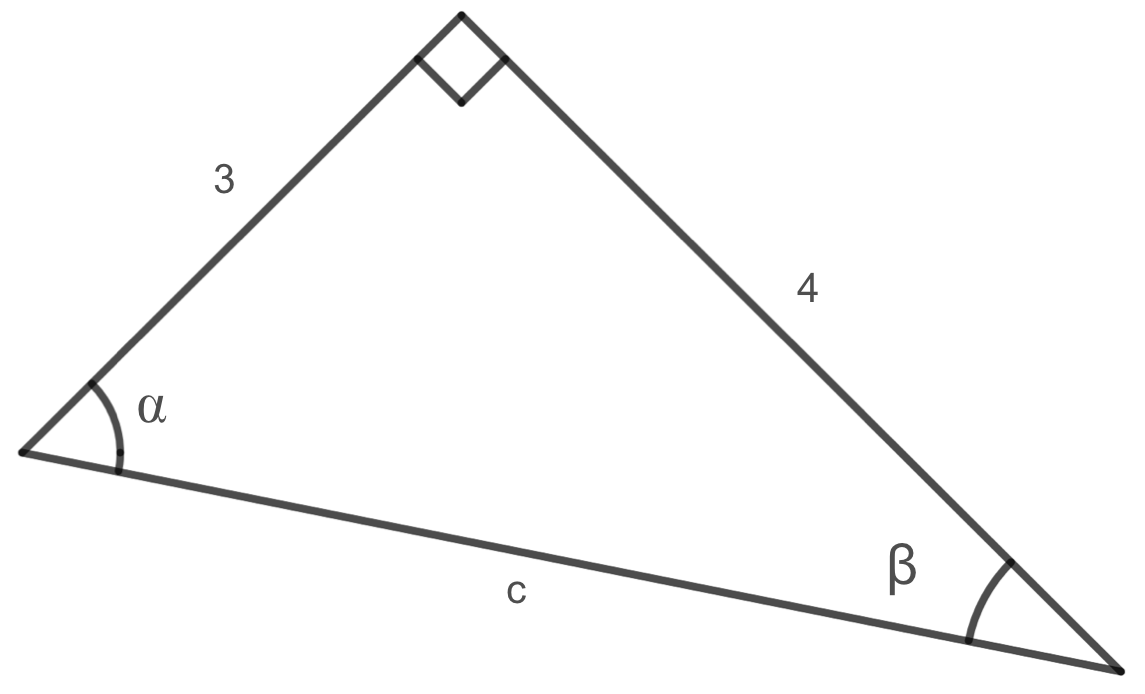
Now solving for the cosine and sine values of \(\alpha\) and \(\beta\text{,}\) we get that
\begin{equation*}
\cos(\alpha) = \frac{\text{adjacent to } \alpha}{\text{hypotenuse}}=\frac{3}{5} \hspace{.5in}
\cos(\beta) = \frac{\text{adjacent to } \beta}{\text{hypotenuse}}=\frac{4}{5}
\end{equation*}
\begin{equation*}
\sin(\alpha) = \frac{\text{opposite to } \alpha}{\text{hypotenuse}}=\frac{4}{5} \hspace{.5in} \sin(\beta) = \frac{\text{opposite to } \beta}{\text{hypotenuse}}=\frac{3}{5}
\end{equation*}
You may have noticed in the previous example that \(\cos(\alpha) = \sin(\beta)\) and \(\cos(\beta) = \sin(\alpha)\text{.}\) If we think about Soh-Cah-Toa and the right triangle relationships, the side opposite of \(\alpha\) is the side that is adjacent to \(\beta\) so it would make sense that \(\cos(\alpha) = \sin(\beta)\text{.}\) Since the three angles in a triangle need to add to \(\pi\text{,}\) or 180 degrees, then the angles \(\alpha\) and \(\beta\) must add to \(\pi/2\text{,}\) or 90 degrees, so \(\alpha + \beta = \pi/2\) and we have that
\begin{equation*}
\beta = \frac{\pi}{2} - \alpha \hspace{.25in} \text{ and } \hspace{.25in} \alpha = \frac{\pi}{2}-\beta
\end{equation*}
Since \(\cos(\alpha) = \sin(\beta)\text{,}\) we get that
\begin{equation*}
\cos(\alpha) = \sin\left(\frac{\pi}{2}-\alpha\right)
\end{equation*}
Cofunctions
Two functions are called cofunctions if they are equal on complementary angles (angles that add up to 90 degrees or \(\pi/2\) radians).
Sine and cosine are examples of cofunctions (hence the "co" in cosine). The cofunction identities for sine and cosine are
\begin{equation*}
\cos(\theta) = \sin\left(\frac{\pi}{2}-\theta\right) \hspace{.25in} \text{ and } \hspace{.25in} \sin(\theta) = \cos\left(\frac{\pi}{2}-\theta\right)
\end{equation*}
Secant and cosecant are another example of cofunctions as are tangent and cotangent, which gives us two more sets of identities.
\begin{equation*}
\sec(\theta) = \csc\left(\frac{\pi}{2}-\theta\right) \hspace{.25in} \text{ and } \hspace{.25in} \csc(\theta) = \sec\left(\frac{\pi}{2}-\theta\right)
\end{equation*}
\begin{equation*}
\tan(\theta) = \cot\left(\frac{\pi}{2}-\theta\right) \hspace{.25in} \text{ and } \hspace{.25in} \cot(\theta) = \tan\left(\frac{\pi}{2}-\theta\right)
\end{equation*}
SubsectionEven and Odd Properties of Trigonometric Functions
Recall that a function is called even if \(f(x)=f(-x)\) for all \(x\) in the domain of \(f\text{.}\) A function is called odd if \(f(x)=-f(-x)\) for all \(x\) in the domain of \(f\text{.}\) If you would like to review these concepts in further detail, please refer to Reflection and Even and Odd Functions.
Now, suppose that \(\theta \) is an angle in the first quadrant. Then recall that the \((x,y)\) coordinates of the corresponding point on the unit circle satisfy the equations
\begin{equation*}
\cos(\theta)=x \hspace{.25in} \text{and} \hspace{.25in} \sin(\theta)=y
\end{equation*}
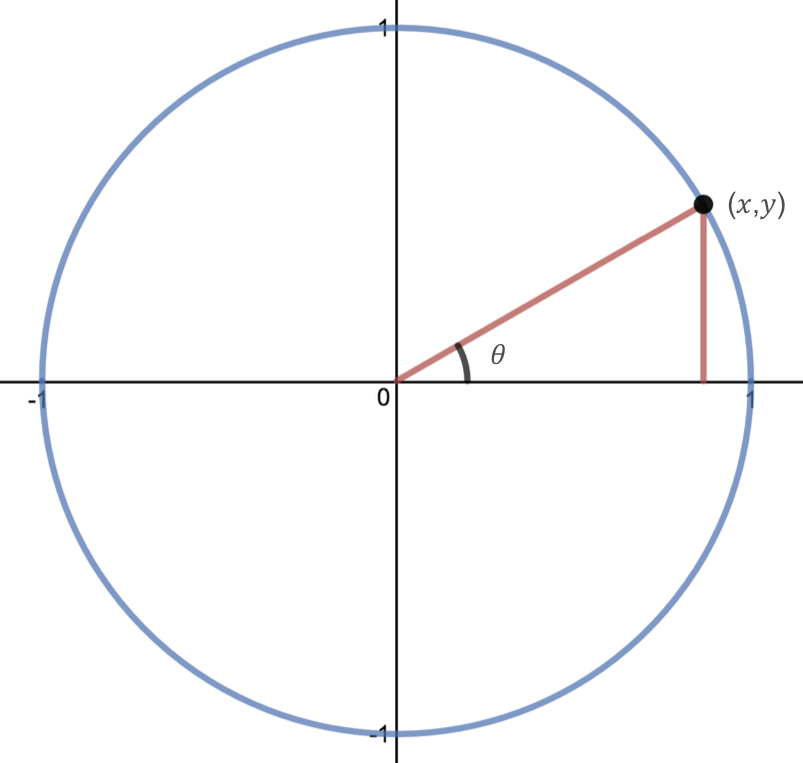
Then if we consider the angle \(-\theta \text{,}\) which is in the fourth quadrant, we can draw the following picture:
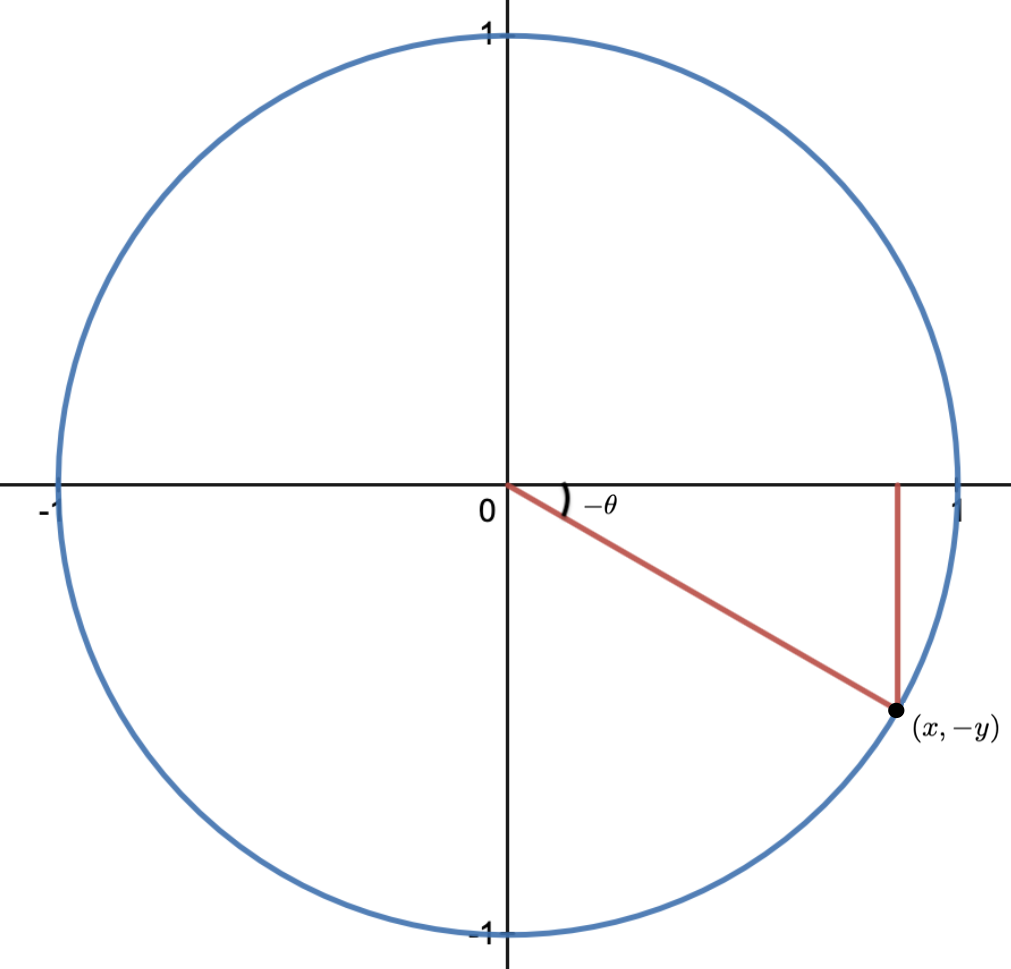
And use it to conclude that
\begin{equation*}
\sin(-\theta) = -y = -\sin(\theta)
\end{equation*}
and
\begin{equation*}
\cos(-\theta) = x = \cos(\theta).
\end{equation*}
As an exercise, you can check that these equations are also true for angles in the second, third, and fourth quadrants. Therefore, we can conclude that sine is an odd function and that cosine is an even function.
We can use the definition of tangent, and the even and odd properties of cosine and sine, respectively, to show that tangent is an odd function:
\begin{equation*}
\begin{aligned}
\tan(-\theta) \amp= \frac{\sin(-\theta)}{\cos(-\theta)} \amp\amp\text{Definition of tangent}\\
\amp= \frac{-\sin(\theta)}{\cos(\theta)} \amp\amp\text{Since sine is odd and cosine is even}\\
\amp= -\left(\frac{\sin(\theta)}{\cos(\theta)}\right) \\
\amp =-\tan(\theta)
\end{aligned}
\end{equation*}
Our findings are summarized below.
Cosine is an even function, i.e.
\begin{equation*}
\cos(-\theta)=\cos(\theta) \text{ for all angles }\theta
\end{equation*}
Sine is an odd function, i.e.
\begin{equation*}
\sin(-\theta)=-\sin(\theta) \text{ for all angles }\theta
\end{equation*}
Tangent is an odd function, i.e.
\begin{equation*}
\tan(-\theta)=-\tan(\theta) \text{ for all angles }\theta
\end{equation*}
Example42
Find \(\sin(-\theta+4\pi)\) given that \(\sin(\theta)=\frac{1}{3}\text{.}\)
Solution
Recall that sine is \(2\pi\) periodic. This means that the value of the sine function is same same whenever the input differs by \(2\pi\text{;}\) in other words, if two angles are coterminal, then they have the same output in the sine function. Therefore
\begin{equation*}
\sin(-\theta+4\pi)=\sin(-\theta+2\pi)=\sin(-\theta)
\end{equation*}
Since sine is a odd function, \(\sin(-\theta)=-\sin(\theta)\text{,}\) so
\begin{equation*}
\sin(-\theta+4\pi)=\sin(-\theta)=-\sin(\theta)=-\frac{1}{3}
\end{equation*}
SubsectionThe Pythagorean Identity
The relationship between right triangles and trigonometric functions of angles on the unit circle can also be used to derive a new identity. Consider the same right triangle we used above.
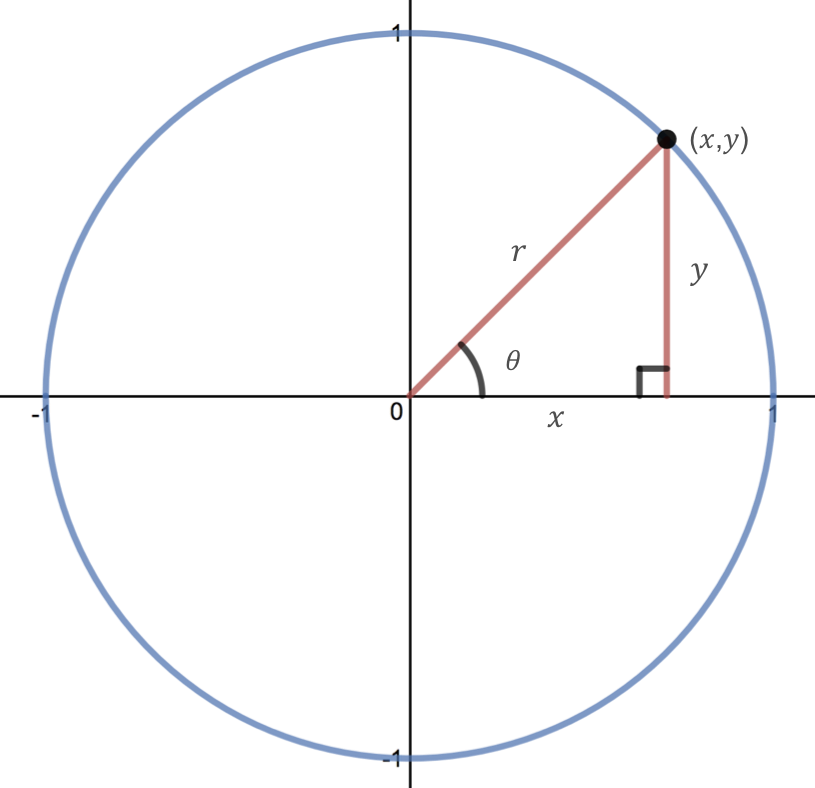
By using the Pythagorean Theorem and the definitions of cosine and sine, we can establish a new identity. We start by relating the sides of the right triangle shown above using the Pythagorean Theorem.
\begin{align*}
x^2+y^2 \amp= r^2 \amp\amp \text{Substituting in } r=1 \\
\\
x^2+y^2 \amp= 1^2 \amp\amp \text{Substituting in } x=\cos(\theta) \text{ and } y=\sin(\theta) \\
\\
(\cos(\theta))^2+(\sin(\theta))^2 \amp= 1^2 \amp\amp \text{Simplifying and using shorthand notation } \\
\\
\cos^2(\theta) + \sin^2(\theta) \amp= 1
\end{align*}
This result is known as the Pythagorean Identity.
Note43
As shown above, \(\cos^2(\theta)\) and \(\sin^2(\theta)\) are commonly used shorthand notations for \((\cos(\theta))^2\) and \((\sin(\theta))^2\text{.}\) Be aware that some calculators and computers may not understand the shorthand notation.
The Pythagorean Identity
For any angle \(\theta\text{,}\)
\begin{equation*}
\cos^2(\theta)+\sin^2(\theta)=1
\end{equation*}
The Pythagorean Identity can help us to find a cosine value of an angle if we know the sine value of that angle or vice versa. However, solving the equation will yield two possible values, so we will need to utilize additional knowledge of the angle to help us find the desired value.
Example44
If \(\displaystyle \sin(\theta)=\frac{3}{7}\) and \(\theta\) is in the second quadrant, find \(\cos(\theta)\text{.}\)
Solution
Substituting the known value for sine into the Pythagorean identity, we have
\begin{align*}
\cos^2(\theta) + \left(\frac{3}{7}\right)^2 \amp= 1 \amp\amp \text{Simplifying}\\
\\
\cos^2(\theta) + \frac{9}{49} \amp= 1 \amp\amp \text{Subtracting } \frac{9}{49} \text{ from both sides}\\
\\
\cos^2(\theta) \amp= \frac{40}{49} \amp\amp \text{Taking the square root of both sides }\\
\\
\cos(\theta) \amp= \pm \sqrt{\frac{40}{49}} \amp\amp \text{Simplifying} \\
\\
\amp= \pm \frac{\sqrt{40}}{7} \\
\\
\amp= \pm \frac{2\sqrt{10}}{7}
\end{align*}
Since \(\theta\) is in the second quadrant, we know the \(x\) value of the corresponding point on the unit circle is negative. Therefore, the cosine value should also be negative. Using this additional information, we can conclude that
\begin{equation*}
\cos(\theta) = -\frac{2\sqrt{10}}{7}
\end{equation*}