MathematicsPreCalculus Mathematics at Nebraska

In the previous section, we used the radius of a circle, \(r\text{,}\) and an angle, \(\theta\) to define polar coordinates. In this section, we use these variables to find the length of arcs on circles.

An arc is a portion of the circumference of a circle.

Arc length is defined as the length of an arc, \(s\text{,}\) along a circle of radius \(r\) subtended (drawn out) by an angle \(\theta\text{.}\)

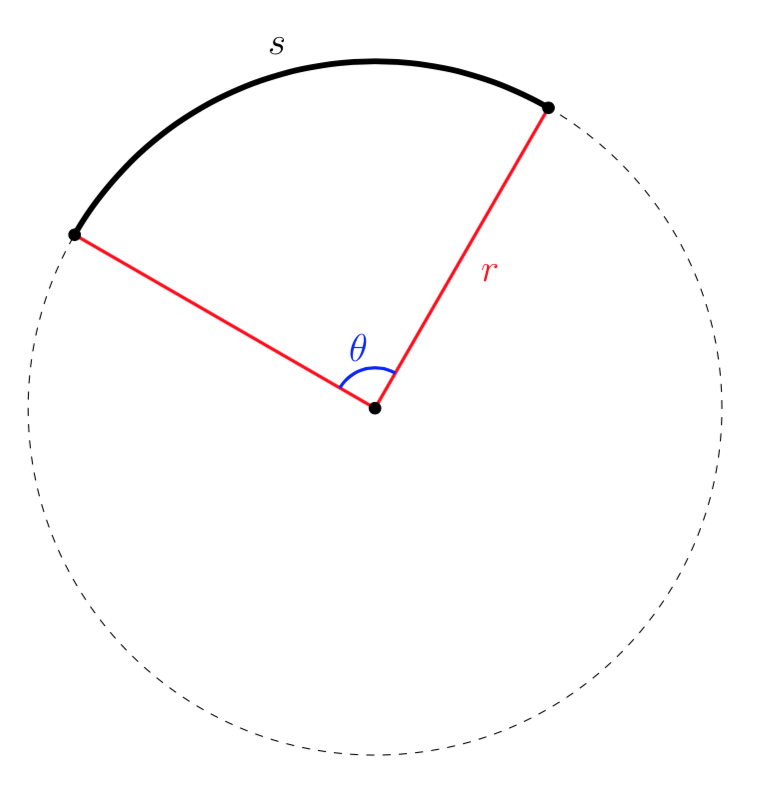
The length of the arc around an entire circle is called the circumference of the circle. The circumference of a circle is

\begin{equation*} C=2\pi r \end{equation*}

To find the length of an arc along a circle of radius \(r\text{,}\) we can think of the arc as a portion of the circumference of the circle. Consider the following example.

Example121

Find the length of an arc on a circle of radius 2 subtended by an angle of 45 degrees.

Solution

Let's start by drawing a picture of the arc and labeling the known information.

We want to find the arc length, \(s\text{,}\) of an arc corresponding to an angle of 45 degrees on a circle of radius 2.

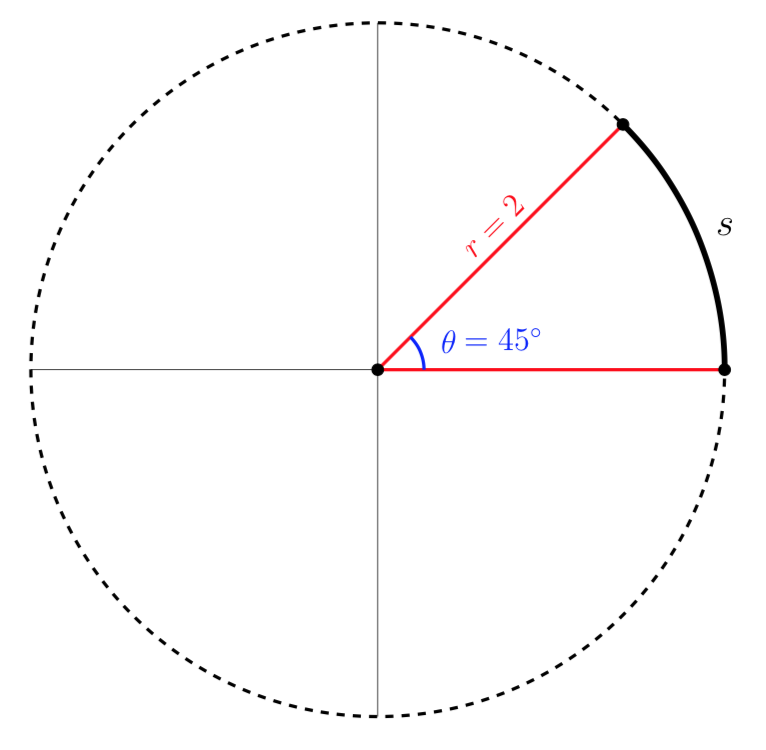
To find the arc length, we can think about the arc as a portion of the circle's circumference. The circumference of the circle is

\begin{equation*} C = 2\pi r = 2\pi \cdot 2 = 4\pi \end{equation*}

Since the arc corresponding to \(45^\circ\) is one-eighth of the full circumference of the circle, the arc length is

\begin{equation*} s = 4\pi \cdot \frac{1}{8} = \frac{4\pi}{8} = \frac{\pi}{2} \end{equation*}

Recall that we defined radians as an angle measurement that arises by looking at angles as a fraction of the unit circle. Since the radius of the unit circle is 1, the circumference of the unit circle is \(2\pi\text{.}\) This is why there are \(2\pi\) radians in one complete trip around a circle. Thus, arc lengths on the unit circle correspond to the angle measures (in radians) that those arcs subtend.

For example, consider an arc subtended by an angle of \(\pi/2\) radians on the unit circle. Since the circumference of the unit circle is \(2\pi\) and the arc is one-fourth of the circumference, the arc length is

This corresponds exactly to the angle subtended by the arc, \(\pi/2\text{.}\)

What if the circle has radius \(r\text{?}\) If the circle is subtended by an angle of \(\theta\) radians, then the arc makes up a fraction of \(\frac{\theta}{2\pi}\) of the whole circumference. Since the circumference is \(2\pi r\text{,}\) we can compute the arc length as follows.