SubsectionParallel and Perpendicular Lines
Parallel lines are lines in the same plane that never intersect. Two different lines in the same plane are parallel if their slopes are the same; in symbols, if the slope of the first line is \(m_1\) and the slope of a different line is \(m_2\text{,}\) then the slopes are parallel if \(m_1=m_2\text{.}\)
Example90
Find an equation of the line passing through \((4,1)\) and parallel to \(x-2y=-2\text{.}\)
SolutionTo find the slope of the given line, solve for \(y\text{.}\)
\begin{equation*}
\begin{aligned}
x-2y\amp =-2\\
-2y\amp = -x-2\\
y\amp =\frac{-x-2}{-2}\\
y\amp = \frac{-x}{-2}-\frac{2}{-2}\\
y\amp =\frac{1}{2}x+1
\end{aligned}
\end{equation*}
Here the given line has slope \(m_1=\frac{1}{2}\text{.}\) The line we are constructing is parallel to this line and will therefore have the same slope, so \(m_2=\frac{1}{2}\text{.}\) Since we are given a point and we now have the slope, we will choose to use point-slope form of a linear equations to determine the slope-intercept form of the equation.
Our point is \((4,1)\) and our slope is \(m=\frac{1}{2}\text{.}\)
\begin{equation*}
\begin{aligned}
y-y_1 \amp= m(x-x_1) \\
y-1 \amp= \dfrac{1}{2}(x-4)
\end{aligned}
\end{equation*}
The equation of the line is given by \(y-1 = \dfrac{1}{2}(x-4)\text{.}\)
It is important to have a geometric understanding of this question. The line we were given, \(x-2y=-2\text{,}\) is shown in blue. The line we constructed, \(y-1=\frac{1}{2}(x-4)\text{,}\) is shown in magenta. notice that the slope is the same at the given line, but they are distinct lines (that is, they do not have the same \(y\)-intercept).
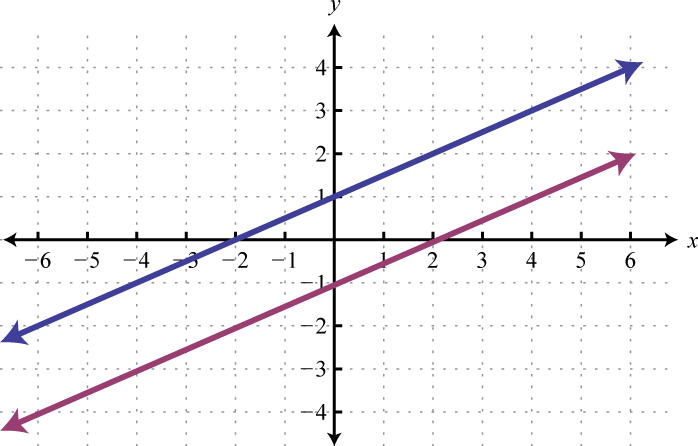
Perpendicular lines are lines in the same plane that intersect at right angles (90 degrees). Two nonvertical lines, in the same plane with slopes \(m_1\) and \(m_2\text{,}\) are perpendicular if the product of their slopes is \(-1\text{,}\) \(m_1\cdot m_2=-1\text{.}\) We can solve for \(m_1\) and obtain \(m_1=-\frac{1}{m_2}\text{.}\) In this form, we see that perpendicular lines have slopes that are opposite reciprocals. In general, given non-zero real numbers \(a\) and \(b\text{,}\) if the slope of the first line is given by \(m_1=\frac{a}{b}\text{,}\) then the slope of the perpendicular line is \(m_2=-\frac{b}{a}\text{.}\)
For example, the opposite reciprocal of \(m_1=-\frac{3}{5}\) is \(m_2=\frac{5}{3}\text{.}\) We can verify that two slopes produce perpendicular lines if their product is \(-1\text{.}\)
\begin{gather*}
m_1\cdot m_2=-\frac{3}{5}\cdot\frac{5}{3}=-\frac{15}{15}=-1
\end{gather*}
Example91
Find an equation of the line passing through \((-5,-2)\) and perpendicular to the graph of \(x+4y=4\text{.}\)
SolutionTo find the slope of the given line, solve for \(y\text{.}\)
\begin{equation*}
\begin{aligned}
x+4y\amp =4\\
4y\amp = -x+4\\
y\amp = \frac{-x+4}{4}\\
y\amp = -\frac{x}{4}+\frac{4}{4}\\
y\amp = -\frac{1}{4}x+1
\end{aligned}
\end{equation*}
The given line has slope \(m_1=-\frac{1}{4}\text{.}\) Since we are constructing a line that is perpendicular to this line, their slopes should be opposite reciprocals, and thus the line we are constructing should have a slope of \(m_2=+\frac{4}{1}=4\text{.}\) Now we can substitute the slope, \(m_2=4\text{,}\) and the given point, \((-5,-2)\text{,}\) into point-slope form:
\begin{equation*}
\begin{aligned}
y-y_1\amp =m(x-x_1)\\
y-(-2)\amp = 4(x-(-5))\\
y+2\amp = 4(x+5)
\end{aligned}
\end{equation*}
The equation of the perpendicular line is given by \(y+2=4(x+5)\text{.}\)
Geometrically, we see that the graph of \(y=4x+18\text{,}\) shown as the dashed line in the graph, passes through \((-5,-2)\) and is perpendicular to the graph of \(y=-\frac{1}{4}x+1\text{.}\)
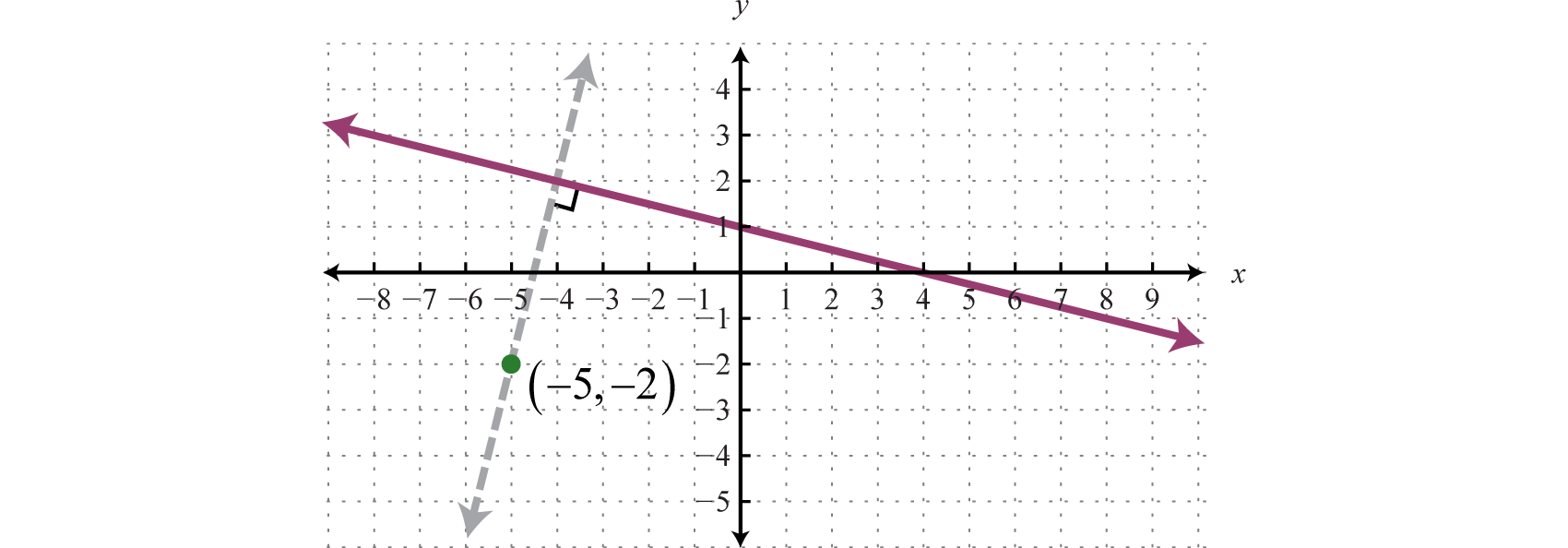
Example92
Find an equation of the line passing through \((-5,-1)\) and perpendicular to \(\frac{1}{3}x-\frac{1}{2}y=-2\text{.}\)
SolutionTo find the slope of the given line, we solve for \(y\text{:}\)
\begin{equation*}
\begin{aligned}
\frac{1}{3}x-\frac{1}{2}y \amp= -2 \\
6\left(\frac{1}{3}x-\frac{1}{2}y\right) \amp= 6(-2) \\
2x - 3y \amp= -12 \\
-3y \amp= -2x - 12 \\
y \amp= \dfrac{2}{3}x + 4
\end{aligned}
\end{equation*}
The given line has slope \(m_1=\frac{2}{3}\text{,}\) therefore the line we are constructing must have a slope of \(m_2=-\frac{3}{2}\text{.}\) Using this and the point \((-5,-1)\text{,}\) we can use point-slope form to write the following equation:
\begin{equation*}
\begin{aligned}
y-(-1) \amp= -\frac{3}{2}(x-(-5)) \\
y+1 \amp- -\frac{3}{2}(x+5)
\end{aligned}
\end{equation*}


