Supplemental Videos
The main topics of this section are also presented in the following videos:
The main topics of this section are also presented in the following videos:
We've been working with the unit circle for quite some time, exploring the relationship between points on the unit circle, the angle made by the line which connects a point on the unit circle to the origin, and the trigonometric function (e.g. sine and cosine) values of said angle.
The unit circle was simply defined to be the circle with radius \(1\) centered at the origin. In this section, we use that definition, along with our knowledge of transformations of functions and their associated graphs, to explore other important geometric shapes.
One way of defining the unit circle is via geometry, the collection of all points that are a distance of one unit from the origin.
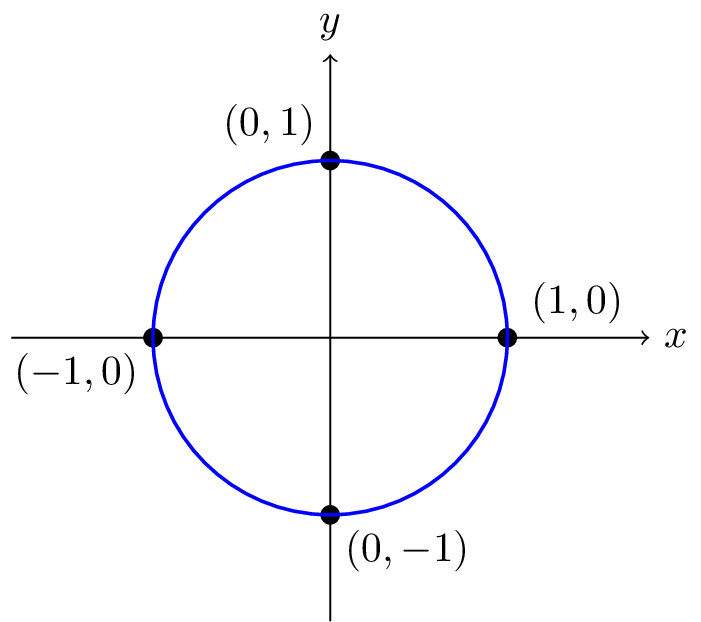
There are also other (equivalent) ways of defining the unit circle. For example, it may be advantageous to define the unit circle analytically, that is, using a formula relating variables \(x\) and \(y\text{.}\) This can be done, and you may have seen the formula before - the unit circle is the collection of all points with \((x,y)\)-coordinates which satisfy the equation
Think about an arbitrary point in the first quadrant of the unit circle:
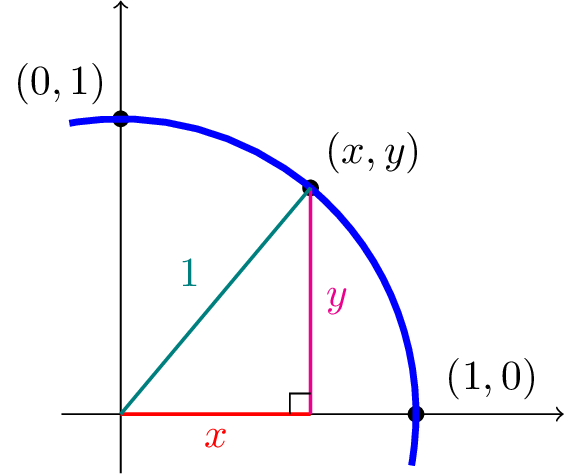
For any such point, we can draw a right triangle whose legs have lengths \(x\) and \(y\text{,}\) as depicted in Figure135. The hypotenuse of the triangle is a line connecting the arbitrary point on the circle, \((x,y)\text{,}\) to the origin, so its length must be \(1\) (as in the definition of the unit circle, the collection of all points a distance of \(1\) from the origin).
What does the Pythagorean Theorem tell us about the relationship among the side lengths of this right triangle? The Pythagorean Theorem says that the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse, i.e. \[ {\color{Red}x}^2 + {\color{Magenta}y}^2 = {\color{OliveGreen}1}^2. \] This aligns perfectly with the equation (1), confirming that our "different ways of representing a circle" are in alignment.
However, we should be a little careful - what about points on the unit circle that are not in the first quadrant? It turns out that equation (1) holds even for \((x,y)\)-coordinate pairs not in the first quadrant; see Example136 for details.
Using the Pythagorean Theorem, find an equation that relates the \((x,y)\)-coordinates depicted in Figure137.
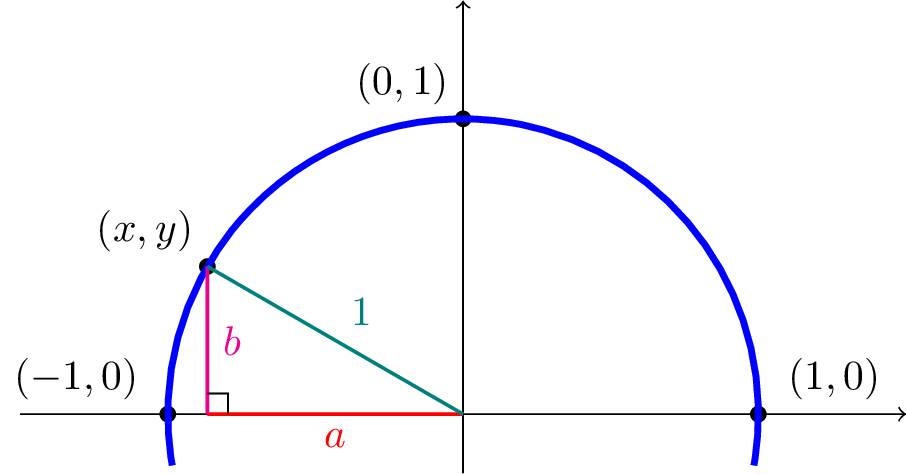
In the picture above, the numbers \(a\) and \(b\) are both positive, since they represent side lengths of a triangle. We know by the Pythagorean Theorem that
Since \((x,y)\) is in the second quadrant, the \(y\)-coordinate of the point \((x,y)\) is positive, and is equal to the length \(b\text{.}\) However, the \(x\)-coordinate is negative, so it cannot be equal to the value \(a\text{!}\) The \(x\)-coordinate is a (positive) distance of \(a\) units to the left of the origin, which means that \(x=-a\text{.}\) Knowing that \(x=-a\) (which means \(a=-x\)) and \(y=b\text{,}\) the equation (2) turns into \begin{align*} (-x)^2 \amp+ (y)^2 = 1 \\ x^2 \amp+ y^2 = 1, \end{align*} all because \((-x)^2=(-x)\cdot(-x)=(-1)^2\cdot x^2=x^2\text{.}\) Even though the \(x\)-coordinate is negative, the "squared" term makes the negative sign disappear, and we confirm that the point on the circle satisfies the equation \(x^2+y^2=1\text{.}\)
In this section, we consider circles in the plane other than the unit circle. For example, we should be able to come up with a formula to describe the following circle.
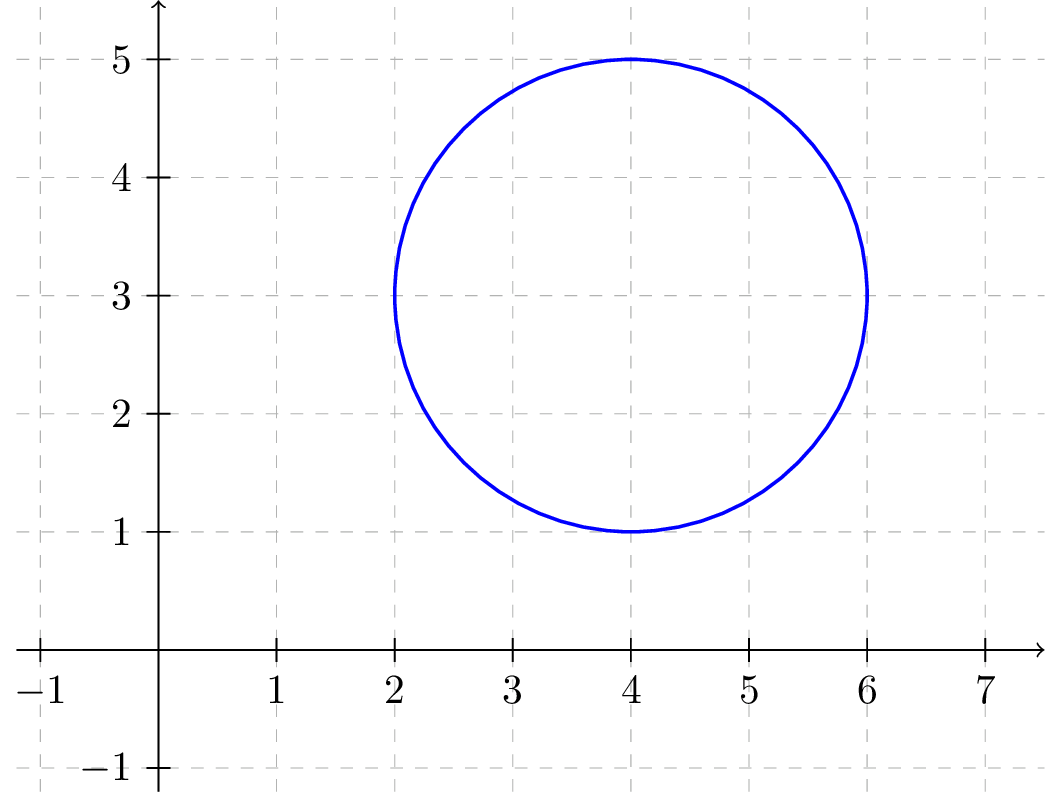
Notice that this circle neither has radius \(1\text{,}\) nor is it centered at the origin. Nonetheless, our knowledge of the unit circle, combined with what we know about general transformations of functions, will be useful for determining formulae to describe general circles in the plane.
As a starting point, let's consider a circle centered at the origin (just like the unit circle) but which has a radius not equal to \(1\text{.}\)
Figure138 below depicts a general circle with radius \(r\) (where \(r\) is some positive real number) centered at the origin, and Figure139 next to it shows a useful right triangle associated with an arbitrary point \((x,y)\) on the circle with radius \(r\) - a right triangle that should look familiar from our work with the unit circle earlier in this section.
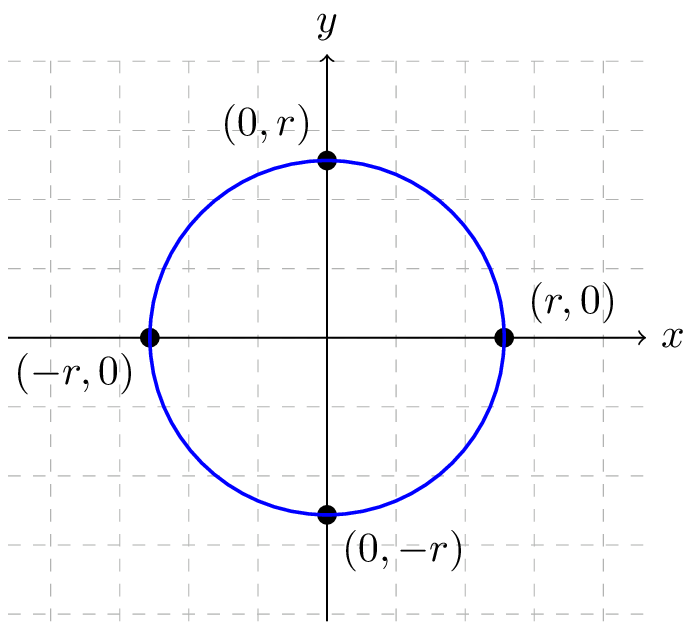
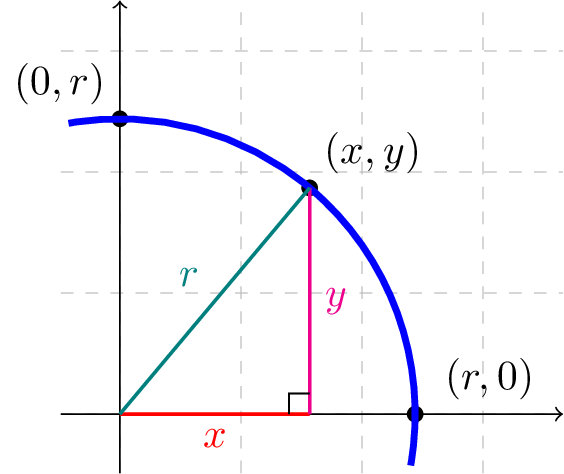
On the unit circle, the hypotenuse of this right triangle was always \(1\text{,}\) but for \((x,y)\) coordinates on a circle of radius \(r\text{,}\) the hypotenuse of the right triangle equals \(r\text{.}\) The Pythagorean Theorem tells us that the quantities \(x\text{,}\) \(y\text{,}\) and \(r\) are related via
Although we have looked at a point \((x,y)\) in the first quadrant, equation (3) holds for points in any quadrant on the circle of radius \(r\) centered at the origin (by the same reasoning as was used for the unit circle previously). We summarize this important formula for circles of arbitrary radius as follows:
A circle of radius \(r\) centered at the origin is the collection of all points which satisfy the equation \[ x^2 + y^2 = r^2 \]
Determine all points on the circle of radius \(8\) centered at the origin whose \(x\)-coordinates are equal to \(5.5\text{.}\)
Start by picturing the circle described (Figure141). Points whose \(x\)-coordinates are equal to \(5.5\) must lie on the vertical line \(x=5.5\) depicted in red in the figure, and we see that this crosses the circle in two spots. We should be able to find two sets of \((x,y)\)-coordinates that satisfy the conditions.
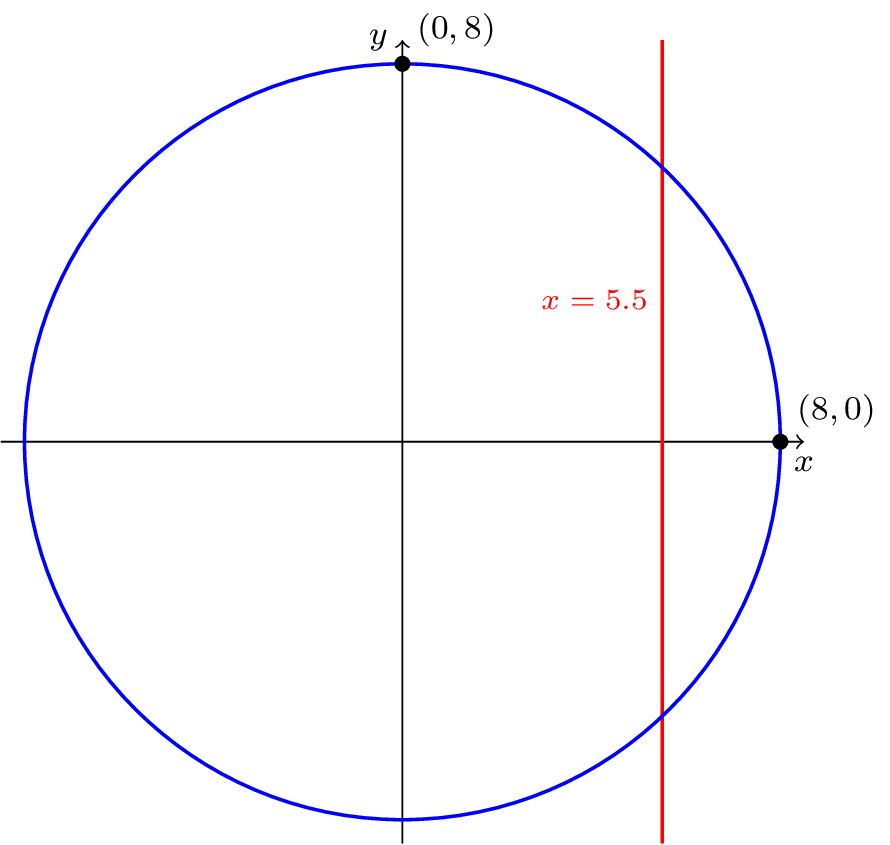
The circle of radius \(8\) centered at the origin is the collection of all points which satisfy the equation
We know that for each point, \(x=5.5\text{.}\) Substituting this in, we are trying to find \(y\) values for which
Solving for \(y^2\) gives
There are supposed to be two distinct solutions, and indeed, there are two distinct values of \(y\) for which \(y^2=33.75\text{.}\) Either \(y=\sqrt{33.75}\) or \(y=-\sqrt{33.75}\text{.}\)
In conclusion, there are two points that lie on the circle of radius \(8\) centered at the origin whose \(x\)-coordinates are equal to \(5.5\text{,}\) and those points are \((5.5,\sqrt{33.75})\) and \((5.5,-\sqrt{33.75})\text{.}\)
We will use our knowledge of transformations of functions (see Section) to come up with formulae for circles not centered at the origin.
First, let's suppose we would like a formula for the circle of radius \(4\) centered at the point \((7,0)\text{.}\)
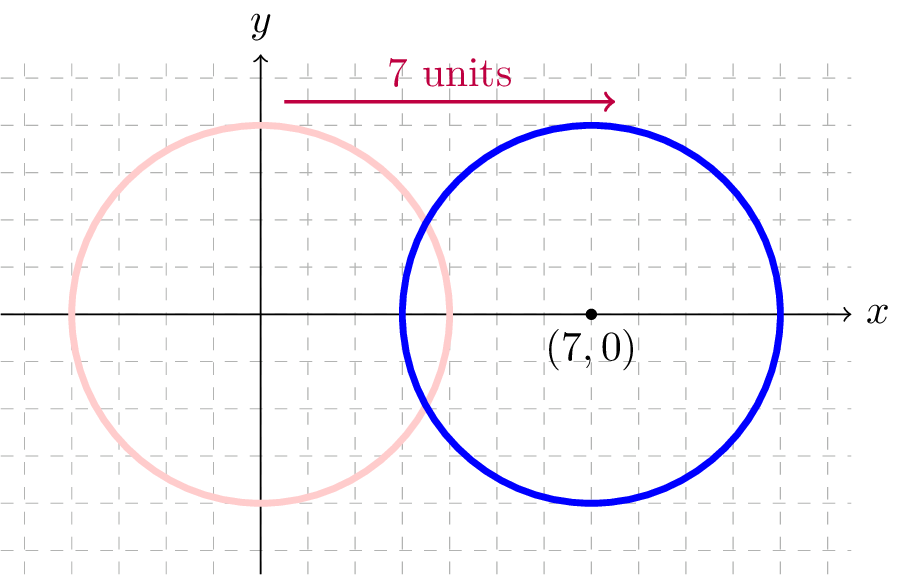
The lighter red circle in Figure142 is centered at the origin, so we know a formula for the points on this circle:
The blue circle in Figure142, the circle of radius \(4\) which is centered at the point \((7,0)\text{,}\) looks identical to the circle whose equation is given by equation (4), just shifted \(7\) units to the right. Our knowledge of transformations of functions tells us that their formulae look very similar, but to shift \(7\) units to the right, replace each variable "\(x\)" in the formula with "\(x-7\)", which gives the formula for the circle of radius \(4\) centered \((7,0)\text{:}\)
We would also like to know what happens to the formula for a circle if it is shifted vertically. Vertical transformations are covered in Section, but in a slightly different context. Section dealt only with explicit functions, that is, functions we could write in the form "\(y=f(x)\)" (where the variable \(y\) is isolated all by itself on one side of the equals sign). The formula for the points on a circle, however, is known as an implicit function because we cannot solve for \(y\) on its own without changing or losing some information about the formula. In this instance, we'll treat vertical shifts just like we handled horizontal shifts, but we change the \(y\) variable instead of the \(x\) variable.
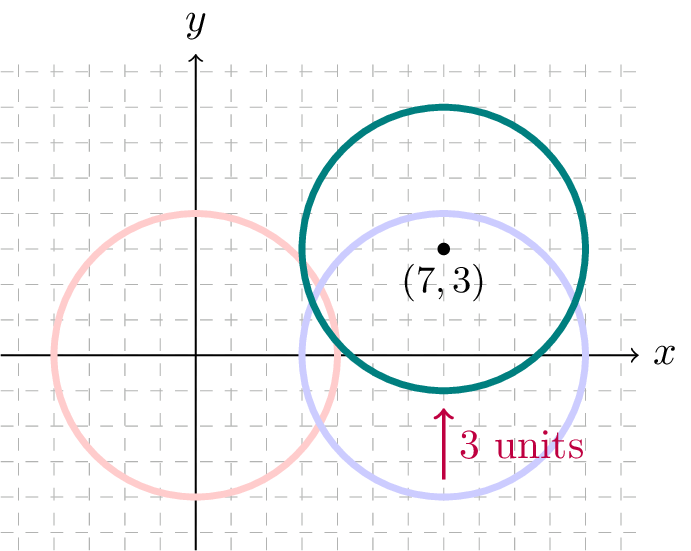
Specifically, if we would like to write down an equation for the circle of radius \(4\) centered at the point \((7,3)\text{,}\) we can make note that this circle is the same as the circle of radius \(4\) centered at the point \((7,0)\) shifted up by \(3\) units (see Figure143). Since we are shifting \(3\) units upward from the circle represented by equation (5), we replace each instance of "\(y\)" with "\(y-3\)" to obtain the formula for the circle of radius \(4\) centered at \((7,3)\text{:}\) \[ (x-7)^2 + (y-3)^2 = 16 \]
The preceding examples generalize to the following result regarding formulae for circles not centered at the origin:
A circle of radius \(r\) centered at the point \((h,k)\) is the collection of all points which satisfy the equation \[ (x-h)^2 + (y-k)^2 = r^2 \]
Note that the definition above works if \(h\) or \(k\) (or both) is negative. For example, the circle of radius \(15\) centered at the point \((-5,-19)\) would be represented by the equation \[ (x-(-5))^2 + (y-(-19))^2 = 15^2, \] which would be simplified to give a more clean formula that represents the circle: \[ (x+5)^2 + (y+19)^2 = 225. \]
Find the center and radius of a circle given by the equation
Recall that a circle of radius \(r\) centered at the point \((h,k)\) is the collection of all points which satisfy the equation
To align with this equation, it must be the case that \(h=2\text{,}\) \(k=-4\text{,}\) and \(r^2=90\text{.}\) This implies that either \(r=\sqrt{90}\) or \(r=-\sqrt{90}\text{.}\) However, in the context of the problem, \(r\) represents the radius of a circle, so it should be a positive value.
We conclude that the equation represents the circle centered at the point \((2,-4)\) which has radius \(\sqrt{90}\text{.}\)
Find the equation of the circle graphed to the right.
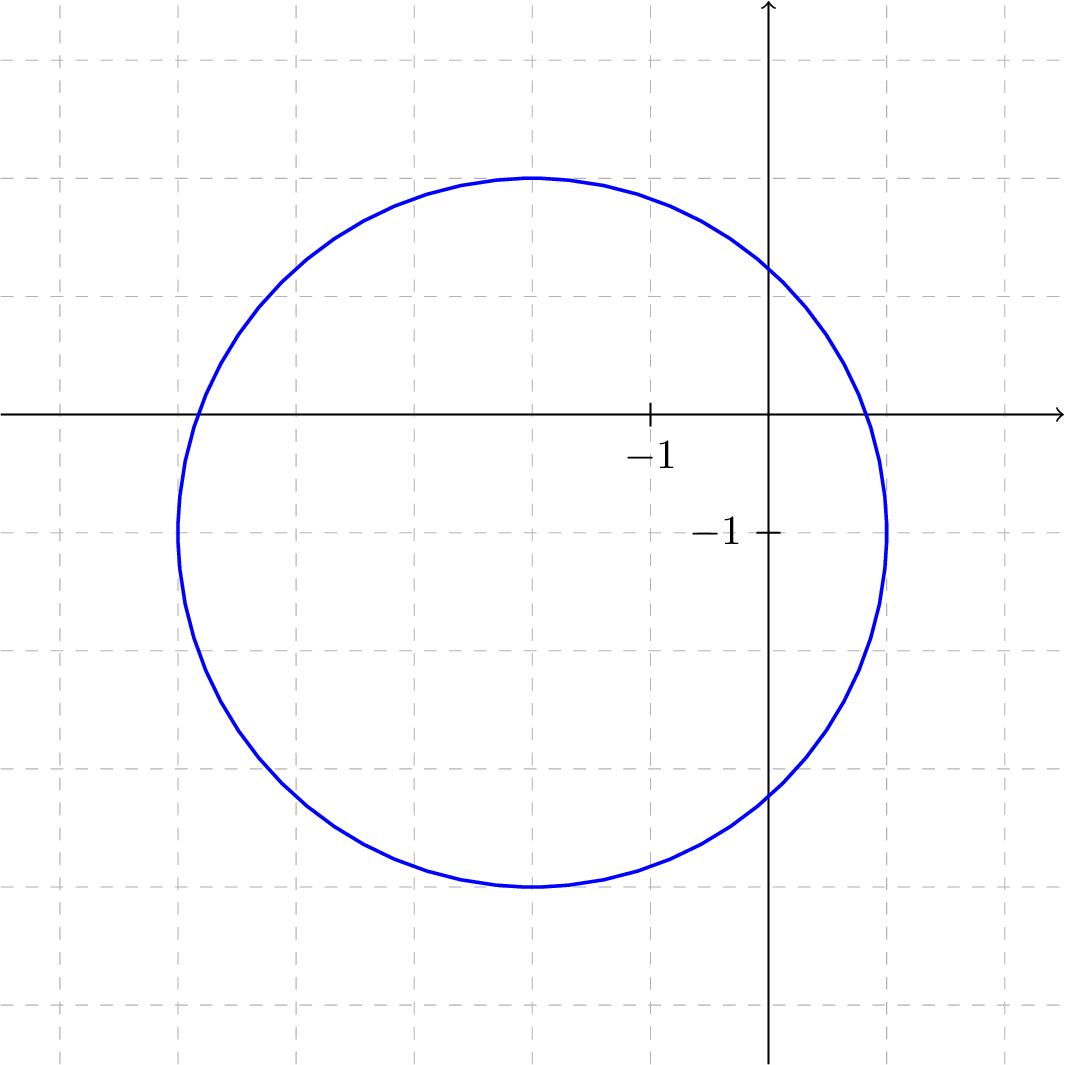
Looking at the picture, the diameter of the circle can be found by measuring the vertical distance between the point at the top of the circle, \((-2,2)\text{,}\) and the point at the bottom of the circle, \((2,-4)\text{.}\) Alternatively, the diameter could be measured by looking at the horizontal distance between \((-5,-1)\) and \((1,-1)\text{.}\) In either case, the diameter is \(6\text{,}\) which implies that the radius of the circle is \(6/2=3\text{.}\)
The center of the circle can be determined by finding the point halfway between the points at the top and bottom of the circle. Moving \(3\) units down from the top point of the circle, we find that the center is located at \((-2,-1)\text{.}\)
Putting everything together, the circle shown is the circle of radius \(3\) centered at the point \((-2,-1)\text{,}\) which is represented by the following equation:
If we take the unit circle and stretch it both vertically and horizontally by exactly the same amount, we end up with a larger circle (that is, a circle with a radius greater than \(1\)). However, we may choose to stretch the unit circle both vertically and horizontally by different factors, and this results in an ellipse.
See an example below, where we take the unit circle and stretch it horizontally by a factor of \(5\) and vertically by a factor of \(3\text{:}\)
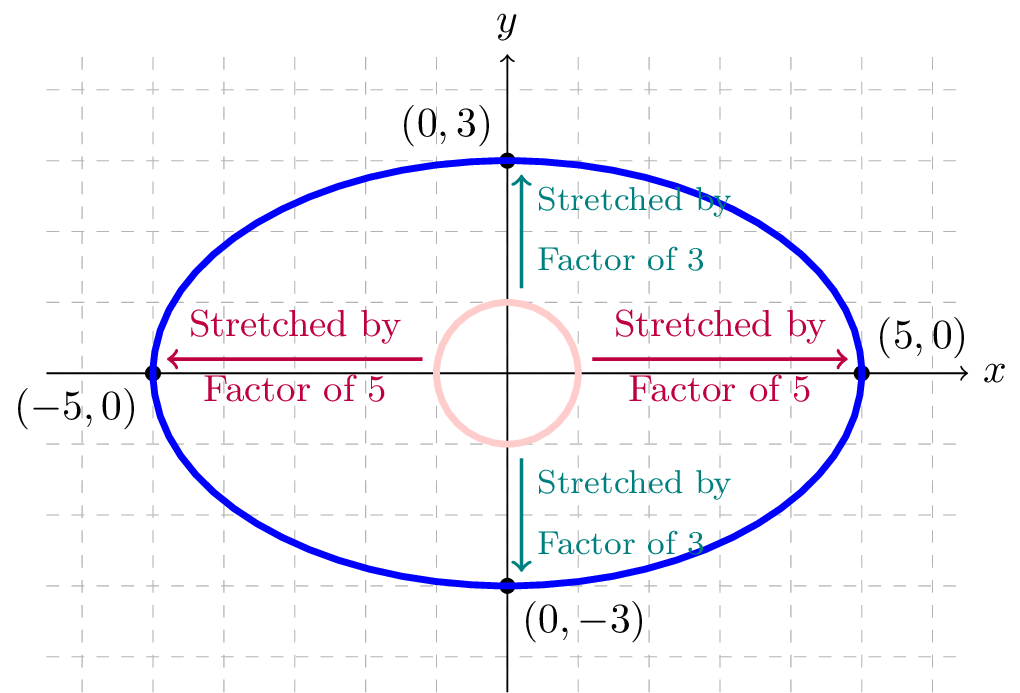
Let's build a formula for this ellipse by again using our knowledge of transformations of functions with the equation of the unit circle, \(x^2+y^2=1\text{.}\)
First, let's consider how the formula must be adjusted to stretch the graph horizontally by a factor of \(5\text{.}\) In order to stretch horizontally, we need to replace each instance of "\(x\)" in the formula with "\(\frac{1}{5}x\)". This is not so intuitive, since we want to stretch the graph by a factor of \(5\text{,}\) but we multiply each \(x\) term by a number smaller than \(1\text{.}\) Nonetheless, as outlined in Section, multiplying each \(x\) term by a factor of \(\frac{1}{5}\) has the result of stretching the graph horizontally by a factor of \(\frac{1}{\sfrac{1}{5}}\text{,}\) which is equal to \(5\text{,}\) as desired.
Because the formula for the unit circle is an implicit formula, we treat our vertical stretch similarly, accomplishing stretching the graph vertically by a factor of \(3\) by replacing each instance of "\(y\)" in the formula with "\(\frac{1}{3}y\)". Thus, the formula that represents the ellipse depicted in Figure146 is given by:
Note the very careful use of parentheses. In the formula for the unit circle, \(x^2+y^2=1\text{,}\) each variable \(x\) and \(y\) is being squared. If we wish to replace, say, each instance of the variable \(x\) with the expression "\(\frac{1}{5}x\)", we must add parentheses to make sure that order of operations is followed appropriately (with \(\frac{1}{5}\) multiplying \(x\) first, then squaring the result).
Although formula (6) perfectly captures the collection of all points that lie on the ellipse depicted in Figure146, it is helpful to do some algebra to obtain another presentation of the formula: \begin{align*} \left( \frac{1}{5} x \right)^2 + \left( \frac{1}{3} y \right)^2 \amp= 1 \\ \left( \frac{x}{5} \right)^2 + \left( \frac{y}{3} \right)^2 \amp= 1 \\ \frac{x^2}{5^2} + \frac{y^2}{3^2} \amp= 1 \end{align*}
Thus, the ellipse centered at the origin which is obtained by stretching the unit circle horizontally by a factor of \({\color{red}5}\) and vertically by a factor of \({\color{blue}3}\) is precisely the collection of \((x,y)\)-coordinates which satisfy the equation \[ \frac{x^2}{{\color{red}5}^2} + \frac{y^2}{{\color{blue}3}^2} = 1. \]
The horizontal and vertical stretch factors used in the previous example could be taken to be any constants, and the result is summarized as follows:
The general equation of an ellipse centered at the origin is the collection of all points which satisfy the equation \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \] where the ellipse is obtained by stretching the unit circle by a factor of \(a\) in the horizontal direction and a factor of \(b\) in the vertical direction.
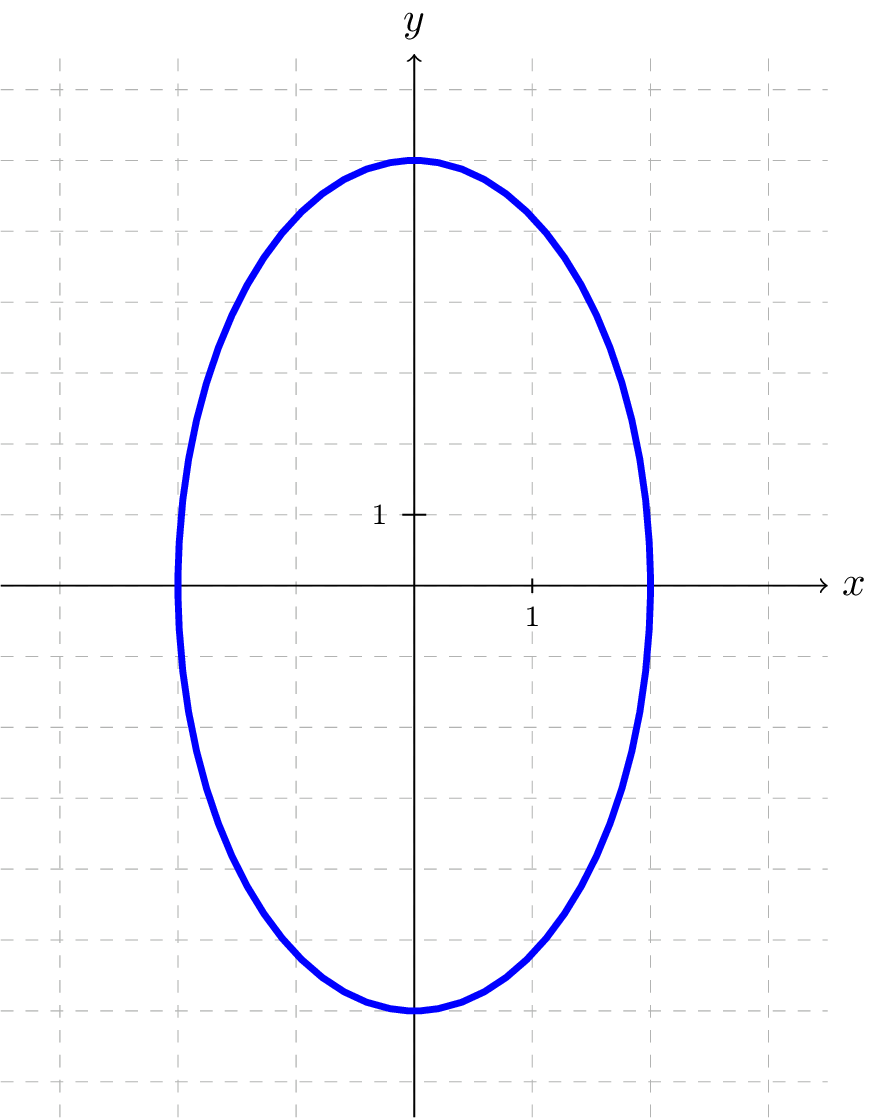
Find the equation of the ellipse graphed to the right.
Recall that an ellipse centered at the origin is the collection of all points which satisfy the equation
where the ellipse is obtained by stretching the unit circle by a factor of \(a\) in the horizontal direction and a factor of \(b\) in the vertical direction.
The ellipse intersects the \(x\)-axis at the points \((-2,0)\) and \((2,0)\text{,}\) so it has been stretched horizontally by a factor of \(2\text{.}\) That is, the \(x\)-coordinates of the points where the unit circle would intersect the \(x\)-axis are \((-1,0)\) and \((1,0)\text{,}\) so each \(x\)-coordinate is multiplied by a factor of \(a=2\text{.}\)
By similar reasoning, since the ellipse intersects the \(y\)-axis at the points \((0,-6)\) and \((0,6)\text{,}\) it has been stretched vertically by a factor of \(b=6\text{.}\)
Using the formula for an ellipse centered at the origin, we find that the ellipse is represented by the equation
A stage is to be built so that the platform is \(20\) feet wide and \(3\) feet tall, and a semiellipse will be placed on top as a backdrop. The base of the semiellipse should be \(1\) foot in from each edge of the stage, and the top of the semiellipse should be a total of \(10\) feet off the ground. A \(6\) ft tall person will be presenting an award and standing \(4.5\) feet off of center-stage. Will their head go above the backdrop?
We start by adding some additional distance labeling based on the problem description with Figure149.
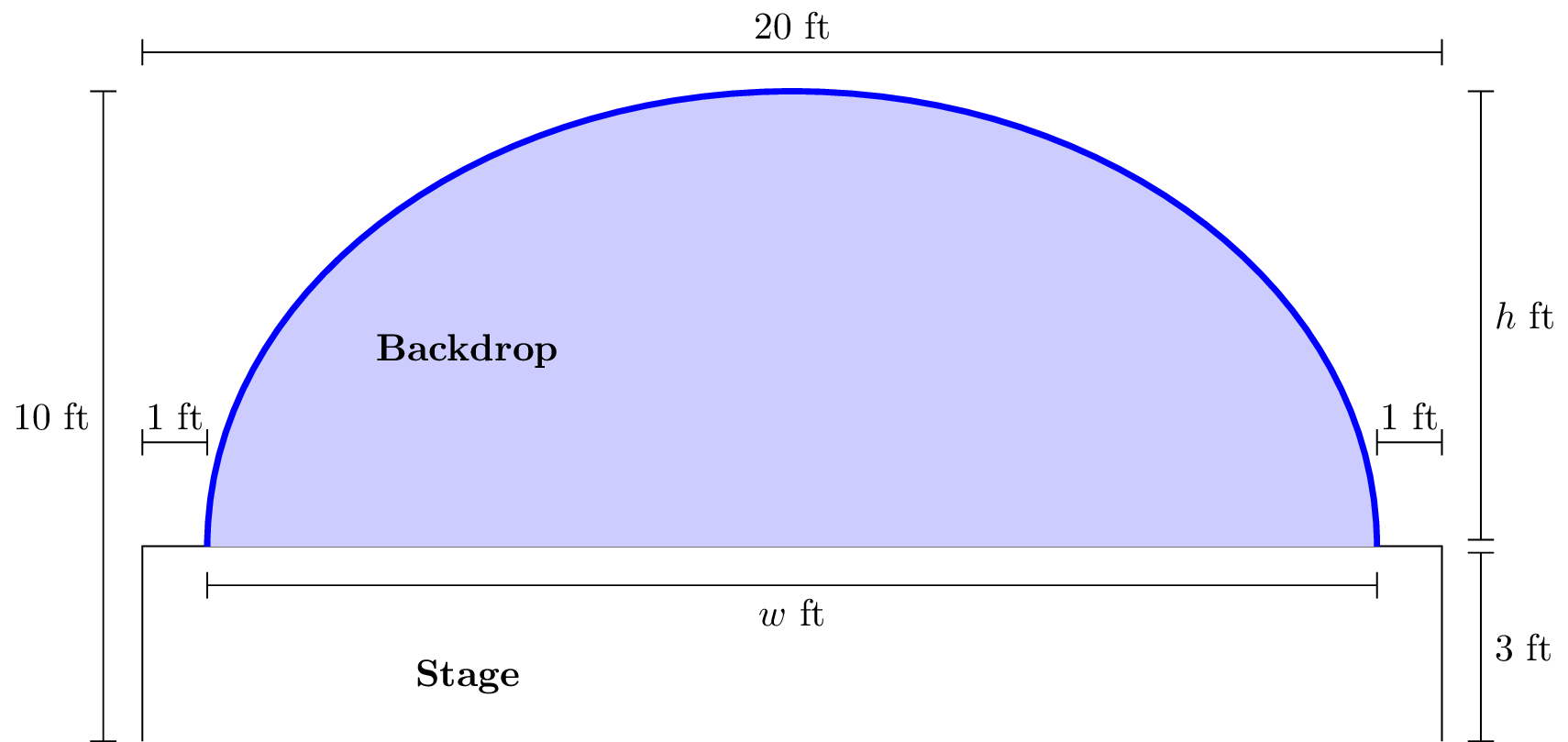
We desire to determine the values of \(h\) and \(w\text{,}\) which would allow us to find an equation to represent the semielliptical backdrop. With this equation, we can determine the exact height of the backdrop where the person will be standing.
The full width of the stage is \(20\) ft, and the backdrop extends exactly \(1\) ft inside either end of the stage, so \(w\) must equal \(20-1-1=18\) ft.
The highest point on the backdrop is \(10\) ft off the ground, and the stage itself is \(3\) ft tall, so the height of the backdrop is \(10-3=7\) ft.
Let's determine an equation to represent the ellipse, imagining the origin situated at the center of the stage (see Figure150). We see that \(b=7\text{,}\) and since the full width of the semiellipse is \(18\text{,}\) we see that \(a=9\text{.}\) With this in mind, the equation which represents this semiellipse is
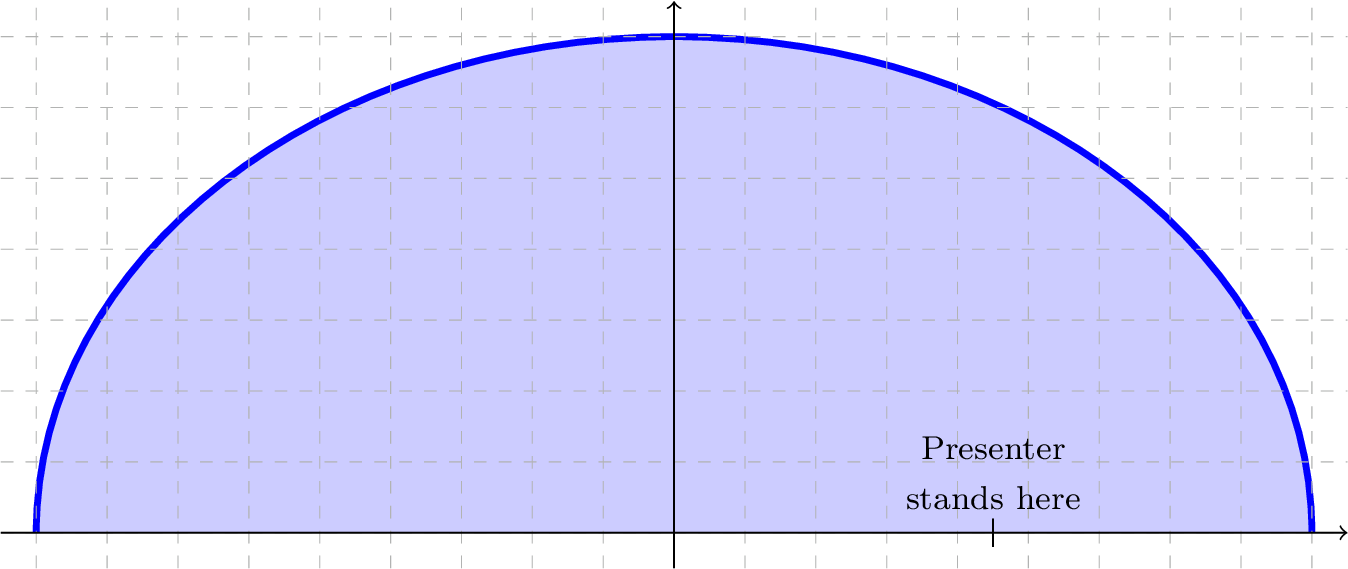
A person will be standing \(4.5\) ft off center-stage (again, see Figure150), so to find the height of the backdrop where they will be standing, we need solve for \(y\) in equation when \(x=2\text{:}\) \begin{align*} \frac{x^2}{81} + \frac{y^2}{49} \amp= 1 \\ \frac{4.5^2}{81} + \frac{y^2}{49} \amp= 1 \\ \frac{y^2}{49} \amp= 1 - \frac{20.25}{81} \\ y^2 \amp= \frac{60.75}{81} \cdot 49 \\ y \amp= \sqrt{ \frac{60.75\cdot49}{81} } \approx 6.06. \end{align*} This means that the backdrop is approximately \(6.06\) ft tall where the presenter will be standing. Since their height is \(6\) ft, their head will not go above the backdrop.
We conclude this section with one final important result about ellipses not centered at the origin. See the formula below which represents a general ellipse centered at any point \((h,k)\text{,}\) generated using the same reasoning as was justified above for a general circle not centered at the origin.
The general equation of an ellipse centered at the point \((h,k)\) is the collection of all points which satisfy the equation \[ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1, \] where the ellipse is obtained by stretching the unit circle by a factor of \(a\) in the horizontal direction and a factor of \(b\) in the vertical direction.