Supplemental Videos
The main topics of this section are also presented in the following videos:
SectionSolving Generalized Equations
In the previous section, we learned how to solve basic trigonometric equations like \(\sin(\theta)=\frac{1}{2}\text{.}\) In this section, we will learn how to solve more complicated trig equations, specifically, generalized trig equations.
SubsectionSolving Generalized Trig Equations
Example84
Solve the trigonometric equation \(2\sin(3\theta)=1\) for all possible values of \(\theta\text{.}\)
Solution
Similar to the examples in the previous section, we can sketch a graph of \(f(\theta)=2\sin(3\theta)\) to see where it intersects with the line \(y=1\text{.}\) Just like before, the angles that correspond to the intersection points of these two functions are the solutions to the equation \(2\sin(3\theta)=1\text{.}\) If we look at the graph, we can see that there are an infinite number of solutions to this equation.
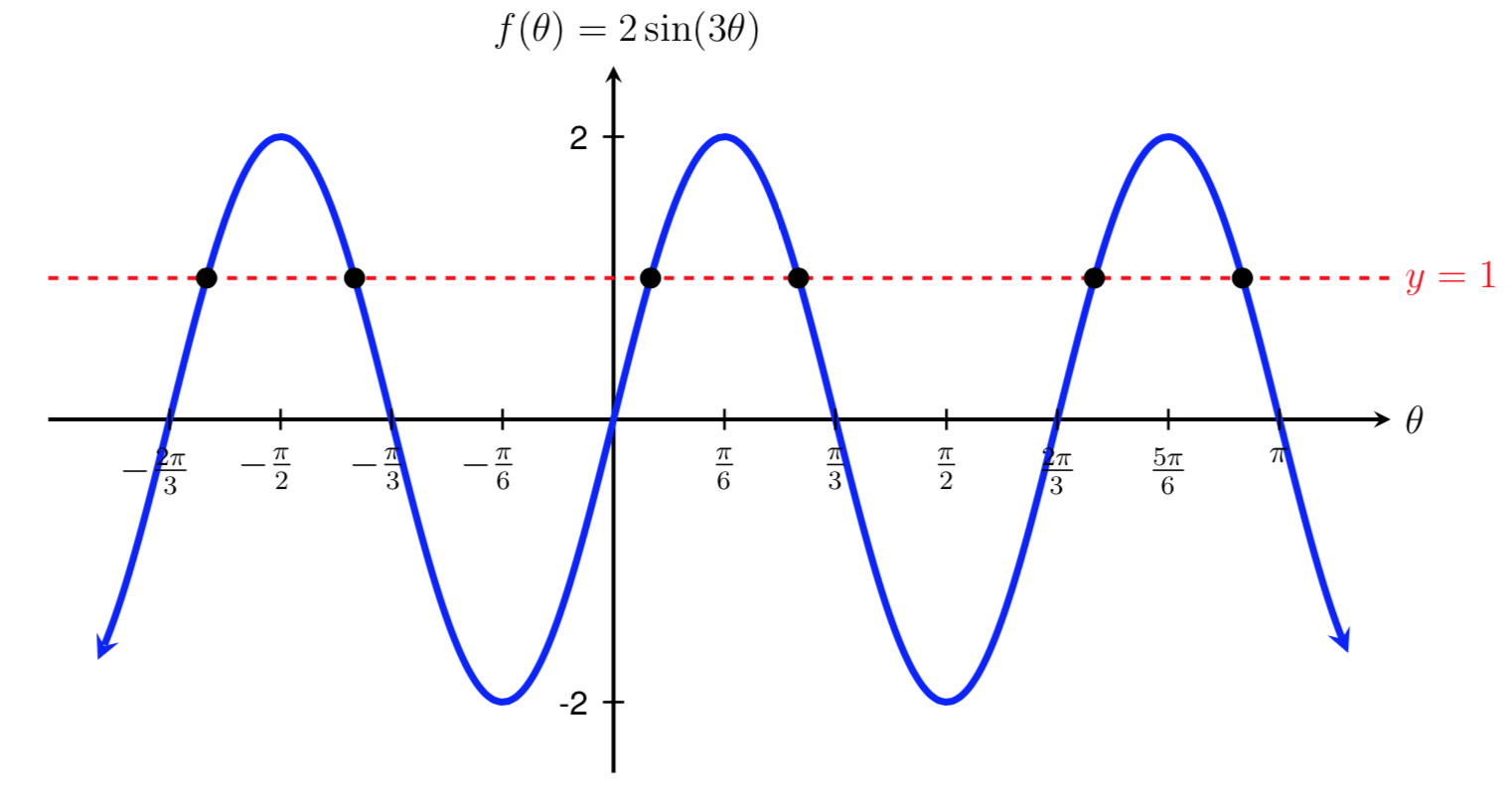
The key difference between this example and examples that we've seen before is that we now have an input of \(3\theta\) instead of just \(\theta\) into our sine function. To solve this equation, we need to identify all angles, \(\theta\text{,}\) such that \(2\sin(3\theta)=1\text{.}\)
To solve this problem, we can first isolate the sine function by dividing each side of the equation by \(2\text{,}\) which gives us
\begin{equation*}
\sin(3\theta)=\frac{1}{2}
\end{equation*}
While we know what angles have a sine value of \(\frac{1}{2}\text{,}\) it is less clear how to proceed when we have \(3\theta\) as our input. To make the problem more familiar, we can introduce a new variable \(\phi\) and set \(\phi=3\theta\text{.}\) Then, substituting \(\phi\) into our equation, we get
\begin{equation*}
\sin(\phi)=\frac{1}{2}
\end{equation*}
In Example77, we found that the solutions to this equation are
\begin{equation*}
\phi = \frac{\pi}{6}+2\pi k \hspace{.25in} \text{and} \hspace{.25in} \phi = \frac{5\pi}{6} + 2\pi k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
Since we want to solve for all possible values of \(\theta\text{,}\) we can use our substitution and replace \(\phi\) with \(3\theta\) in the solutions above. Therefore, we have that
\begin{equation*}
3\theta = \frac{\pi}{6}+2\pi k \hspace{.25in} \text{and} \hspace{.25in} 3\theta = \frac{5\pi}{6} + 2\pi k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
Our final step in solving for \(\theta\) is to divide each side of the equations by \(3\text{,}\) so we have
\begin{equation*}
\theta = \frac{\frac{\pi}{6}+2\pi k}{3} \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{\frac{5\pi}{6} + 2\pi k}{3} \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
and simplifying we get
\begin{equation*}
\theta = \frac{\pi}{18}+\frac{2\pi}{3} k \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{5\pi}{18} + \frac{2\pi}{3} k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
Notice that when we divide the right side of our equations by \(3\text{,}\) we must divide each term by \(3\) in order to simplify the equations. Therefore, we end up adding multiples of \(\frac{2\pi}{3}\) to our initial solutions instead of multiples of \(2\pi\text{.}\) Also note that the sine function we are dealing with, \(f(\theta)=2\sin(3\theta)\text{,}\) has a period of \(\frac{2\pi}{3}\text{.}\)
Example85
Solve the trigonometric equation \(2\sin(3(x-2)) = 1\) for all possible values of \(x\text{.}\)
SolutionTo solve this problem, we can first isolate the sine function by dividing each side of the equation by \(2\text{,}\) which give us
\begin{equation*}
\sin(3(x-2)) = \frac{1}{2}
\end{equation*}
Set \(\phi = 3(x-2)\text{.}\) Then, substituting \(\phi\) into our new equation, we get
\begin{equation*}
\sin(\phi) = \frac{1}{2}
\end{equation*}
In Example77, we found that the solutions to this equation are
\begin{equation*}
\phi = \frac{\pi}{6}+2\pi k \hspace{.25in} \text{and} \hspace{.25in} \phi = \frac{5\pi}{6} + 2\pi k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
We can use our substitution and replace \(\phi\) with \(3(x-2)\) in the solutions above. Therefore, we have that
\begin{equation*}
3(x-2) = \frac{\pi}{6}+2\pi k \hspace{.25in} \text{and} \hspace{.25in} 3(x-2) = \frac{5\pi}{6} + 2\pi k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
We need to solve for \(x\text{.}\) To isolate the \(x\text{,}\) let's divide each side of the equations by \(3\text{.}\) Doing so and simplifying gives us
\begin{equation*}
x-2 = \frac{\pi}{18}+\frac{2\pi}{3} k \hspace{.25in} \text{and} \hspace{.25in} x-2 = \frac{5\pi}{18} + \frac{2\pi}{3} k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
Our final step in solving for \(x\) is to add \(2\) to each of the equations, so the solutions are:
\begin{equation*}
x = 2+\frac{\pi}{18}+\frac{2\pi}{3} k \hspace{.25in} \text{and} \hspace{.25in} x = 2+\frac{5\pi}{18} + \frac{2\pi}{3} k \hspace{.25in} \text{ where } k \text{ is any integer}
\end{equation*}
Example86
Solve the trigonometric equation \(\tan(\frac{1}{5}(x+4)) = 3\) for all possible values of \(x\text{.}\)
SolutionFor this problem, the tangent function has already been isolated. So, set \(\phi = \frac{1}{5}(x+4)\text{.}\) Then, substituting \(\phi\) into the equation gives us \(\tan(\phi) = 3\text{.}\) We then take the inverse tangent to both sides of the equation. Doing so give us \(\phi = \tan^{-1}(3)\text{.}\)
Using a calculator, we find that
\begin{equation*}
\phi \approx 1.249
\end{equation*}
To get all solutions for \(\phi\text{,}\) recall that the tangent function has period \(\pi\text{.}\) Hence,
\begin{equation*}
\phi \approx 1.249 + \pi k
\end{equation*}
where \(k\) is an integer.
Now, if we undo the substitution, we have that
\begin{equation*}
\frac{1}{5}(x+4) \approx 1.249 + \pi k\text{.}
\end{equation*}
We can then use simple algebra to solve for \(x\) from this equation. Let's start by multiplying both sides by \(5\text{.}\) This gives us
\begin{equation*}
x+4 \approx 5(1.249 + \pi k)
\end{equation*}
Next, we subtract \(4\) to both sides of the previous equation. Then,
\begin{equation*}
x \approx 5(1.249 + \pi k) - 4
\end{equation*}
Therefore, the solutions to the trig equation is given by
\begin{equation*}
x \approx 5(1.249 + \pi k) - 4, \ \text{ or equivalently, } \ x \approx 2.245 + 5\pi k, \text{ where } \ k \ \text{ is an integer.}
\end{equation*}