SubsectionEquations of Lines
Given the algebraic equation of a line, we can graph it in a number of ways. In this section, we will be given a geometric description of a line and find the algebraic equation. Finding an equation of a line can be accomplished in a number of ways. The following example makes use of slope-intercept form, \(y=mx+b\text{,}\) or using function notation, \(f(x)=mx+b\text{.}\) If we can determine the slope, \(m\text{,}\) and the \(y\)-intercept, \((0,b)\text{,}\) we can then construct an equation.
Example82
Find an equation of the line passing through \((-3,6)\) and \((5,-4)\text{.}\)
SolutionWe begin by finding the slope. Given two points, we can find the slope using the slope formula.
\begin{equation*}
\begin{aligned}
m\amp = \frac{y_2-y_1}{x_2-x_1}\\
\amp =\frac{-4-(6)}{5-(-3)}\\
\amp =\frac{-4-6}{5+3}\\
\amp =\frac{-10}{8}\\
\amp = -\frac{5}{4}
\end{aligned}
\end{equation*}
Here \(m=-\frac{5}{4}\) and we have
\begin{equation*}
\begin{aligned}
f(x)\amp =mx+b\\
f(x)\amp = -\frac{5}{4}x+b.
\end{aligned}
\end{equation*}
To find \(b\text{,}\) substitute either one of the given points through which the line passes. Here we will use \((-3,6)\text{,}\) but \((5,-4)\) would work just as well:
\begin{equation*}
\begin{aligned}
f(x)\amp = -\frac{5}{4}x+b\amp \alert{\text{Use }(x,f(x))=(-3,6)}\\
\alert{6}\amp = -\frac{5}{4}(\alert{-3})+b\\
6\amp =\frac{15}{4}+b\\
\frac{6\cdot \alert{4}}{1\cdot\alert{4}}-\frac{15}{4}\amp =b\\
\frac{24-15}{4}\amp =b\\
\frac{9}{4}\amp =b
\end{aligned}
\end{equation*}
Therefore, the equation of the line passing through the two given points is \(f(x)=mx+b=-\frac{5}{4}x+\frac{9}{4}\text{.}\)
Next, we outline an alternative method for finding equations of lines. Begin by applying the slope formula with a given point \((x_1,y_1)\) and a variable point \((x,y)\text{.}\)
\begin{align*}
m\amp =\frac{y-y_1}{x-x_1}\\
\frac{m}{1}\amp =\frac{y-y_1}{x-x_1}\\
m(x-x_1)\amp = y-y_1\\
y-y_1\amp = m(x-x_1)
\end{align*}
Therefore, the equation of a nonvertical line can be written in point-slope form:
\begin{gather*}
y-y_1=m(x-x_1)
\end{gather*}
Point-slope form is particularly useful for finding an equation of a line given the slope and any ordered pair solution. After finding the slope, \(-\frac{5}{4}\) in the previous example, we could use this form to find an equation. Using the point \((-3,6)\text{,}\) we substitute as follows:
\begin{align*}
y-y_1\amp =m(x-x_1)\\
y-(\alert{6})\amp =\alert{-\frac{5}{4}}(x-(\alert{-3}))\\
y-6\amp =-\frac{5}{4}(x+3)\\
y-6\amp=-\frac{5}{4}x-\frac{15}{4}\\
y\amp =-\frac{5}{4}x-\frac{15}{4}+6\\
y\amp =-\frac{5}{4}x+\frac{9}{4}
\end{align*}
Notice that we obtain the same linear function \(f(x)=-\frac{5}{4}x+\frac{9}{4}\text{.}\)
Note: Sometimes a variable is not expressed explicitly in terms of another; however, it is still assumed that one variable is dependent on the other. For example, the equation \(2x+3y=6\) implicitly represents the function \(f(x)=-\frac{2}{3}x+2\text{.}\) You should become comfortable with working with functions in either form.
Example83
Find an equation of the following linear function:
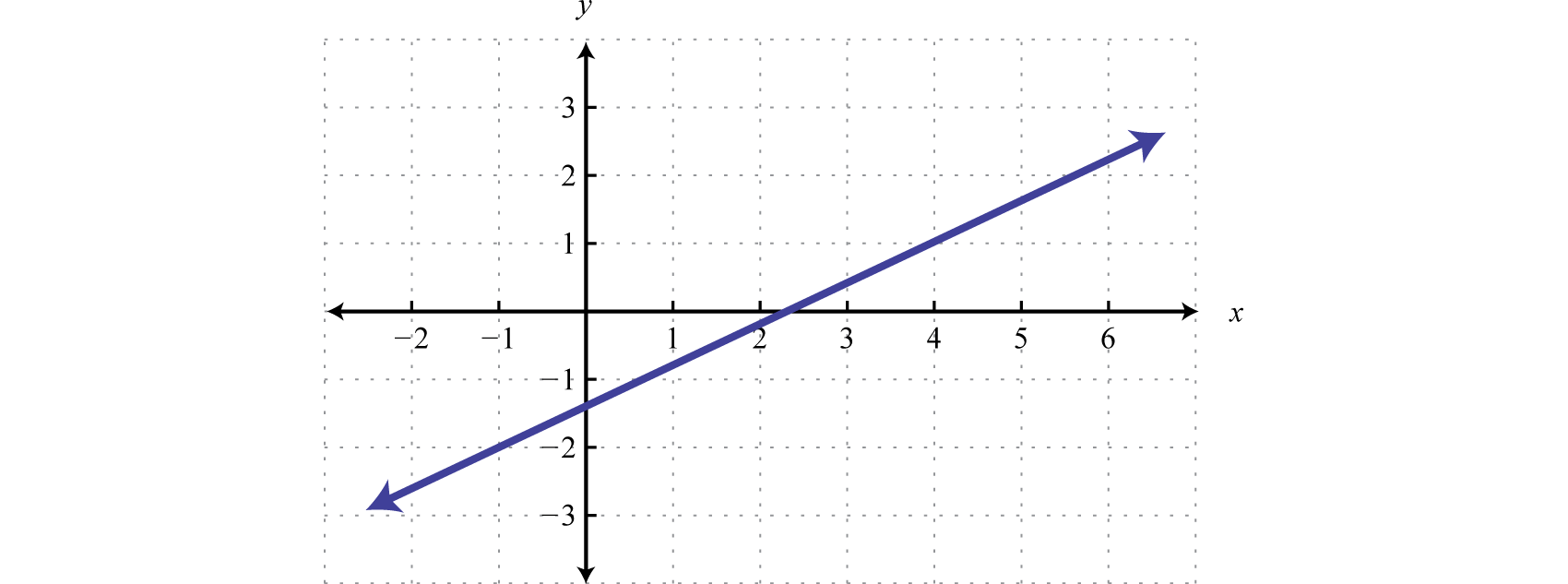
SolutionFrom the graph we can determine two points \((-1, -2)\) and \((4, 1)\text{.}\) Use these points to read the slope from the graph. The rise is \(3\) units and the run is \(5\) units.
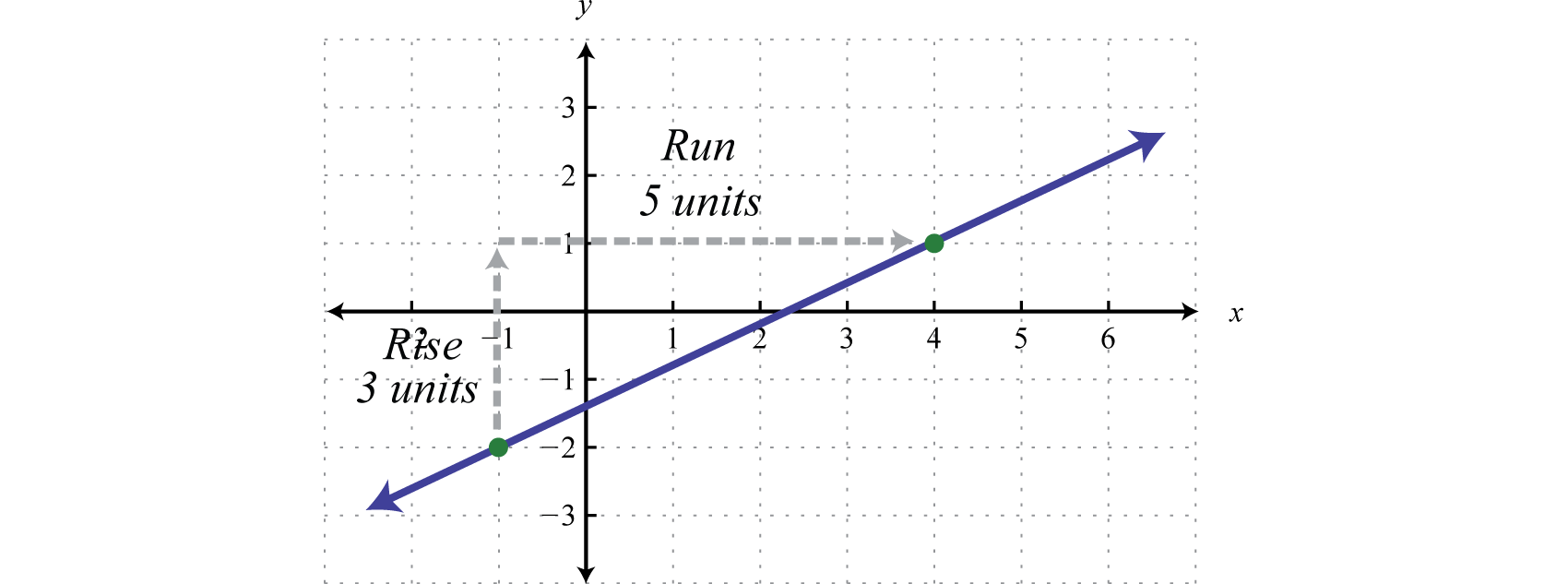
Therefore, we have the slope and a point. (It does not matter which of the given points we use, the result will be the same.) We will use the point \((-1,-2)\) with our slope \(m=\frac{3}{5}\text{.}\)
We will use point-slope form to determine an equation of the line.
\begin{equation*}
\begin{aligned}
y-y_1\amp =m(x-x_1)\\
y-(\alert{-2})\amp -\alert{\frac{3}{5}}(x-(\alert{-1}))\\
y+2\amp = \frac{3}{5}(x+1)\\
y+2\amp = \frac{3}{5}x+\frac{3}{5}\\
y\amp =\frac{3}{5}x+\frac{3}{5}-2\\
y\amp =\frac{3}{5}x-\frac{7}{5}
\end{aligned}
\end{equation*}
An equation of the line is given by \(y=\frac{3}{5}x-\frac{7}{5}\) or \(f(x)=\frac{3}{5}x-\frac{7}{5}\text{.}\)
Parallel lines are lines in the same plane that never intersect. Two different, non-vertical, lines in the same plane with slopes \(m_1\) and \(m_2\) are parallel if their slopes are the same, \(m_1=m_2\text{.}\)
Example84
Find an equation of the line passing through \((4,1)\) and parallel to \(x-2y=-2\text{.}\)
SolutionTo find the slope of the given line, solve for \(y\text{.}\)
\begin{equation*}
\begin{aligned}
x-2y\amp =-2\\
-2y\amp = -x-2\\
y\amp =\frac{-x-2}{-2}\\
y\amp = \frac{-x}{-2}-\frac{2}{-2}\\
y\amp =\frac{1}{2}x+1
\end{aligned}
\end{equation*}
Here the given line has slope \(m_1=\frac{1}{2}\) and thus the slope of a parallel line is given by \(m_2=\frac{1}{2}\text{.}\) Since we are given a point and we now have the slope, we will choose to use point-slope form of a linear equations to determine the slope-intercept form of the equation.
Our point is \((4,1)\) and our slope is \(m=\frac{1}{2}\text{.}\)
\begin{align*}
y-y_1\amp =m(x-x_1)\\
y-(1)\amp =\frac{1}{2}(x-4)\\
y-1\amp =\frac{1}{2}x-\frac{4}{2}\\
y-1\alert{+1}\amp =\frac{1}{2}x-2\alert{+1}\\
y\amp = \frac{1}{2}x-1
\end{align*}
The equation of the line is given by \(y=\frac{1}{2}x-1\text{,}\) or \(f(x)=\frac{1}{2}x-1\text{.}\)
It is important to have a geometric understanding of this question. We were asked to find an equation of a line parallel to another line passing through a certain point.
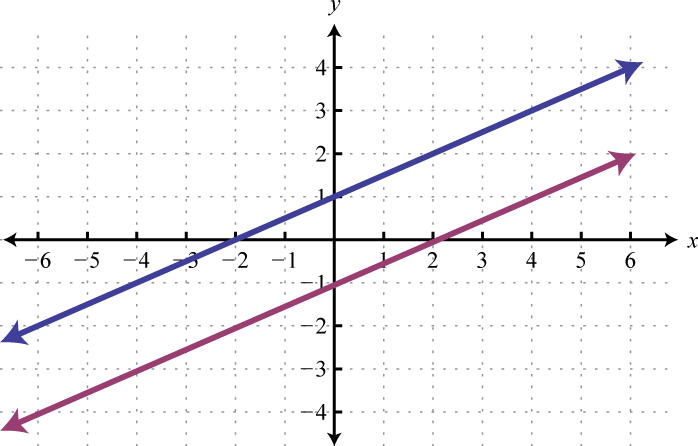
Through the point \((3,-\frac{1}{2})\) we have a parallel line, \(y=\frac{1}{2}x-1\text{,}\) shown as a magenta line. Notice that the slope is the same as the given line, \(y=\frac{1}{2}x+1\text{,}\) but the \(y\)-intercept is different.
Perpendicular lines are lines in the same plane that intersect at right angles (90 degrees). Two nonvertical lines, in the same plane with slopes \(m_1\) and \(m_2\text{,}\) are perpendicular if the product of their slopes is \(-1\text{,}\) \(m_1\cdot m_2=-1\text{.}\) We can solve for \(m_1\) and obtain \(m_1=-\frac{1}{m_2}\text{.}\) In this form, we see that perpendicular lines have slopes that are negative reciprocals, or opposite reciprocals. In general, given non-zero real numbers \(a\) and \(b\text{,}\) if the slope of the first line is given by \(m_1=\frac{a}{b}\text{,}\) then the slope of the perpendicular line is \(m_2=-\frac{b}{a}\text{.}\)
For example, the opposite reciprocal of \(m_1=-\frac{3}{5}\) is \(m_2=\frac{5}{3}\text{.}\) We can verify that two slopes produce perpendicular lines if their product is \(-1\text{.}\)
\begin{gather*}
m_1\cdot m_2=-\frac{3}{5}\cdot\frac{5}{3}=-\frac{15}{15}=-1
\end{gather*}
Example85
Find an equation of the line passing through \((-5,-2)\) and perpendicular to the graph of \(x+4y=4\text{.}\)
SolutionTo find the slope of the given line, solve for \(y\text{.}\)
\begin{equation*}
\begin{aligned}
x+4y\amp =4\\
4y\amp = -x+4\\
y\amp = \frac{-x+4}{4}\\
y\amp = -\frac{x}{4}+\frac{4}{4}\\
y\amp = -\frac{1}{4}x+1
\end{aligned}
\end{equation*}
The given line has slope \(m_1=-\frac{1}{4}\) and thus, \(m_2=+\frac{4}{1}=4\text{.}\) Substitute this slope and the given point into point-slope form.
Our point is \((-5,-2)\) and our slope is \(m_2=4\text{.}\)
\begin{equation*}
\begin{aligned}
y-y_1\amp =m(x-x_1)\\
y-(-2)\amp = 4(x-(-5))\\
y+2\amp = 4(x+5)\\
y+2\amp = 4x+20\\
y\amp = 4x+18
\end{aligned}
\end{equation*}
The equation of the perpendicular line is given by \(y=4x+18\text{,}\) or \(f(x)=4x+18\text{.}\)
Geometrically, we see that the graph of \(y=4x+18\text{,}\) shown as the dashed line in the graph, passes through \((-5,-2)\) and is perpendicular to the graph of \(y=-\frac{1}{4}x+1\text{.}\)
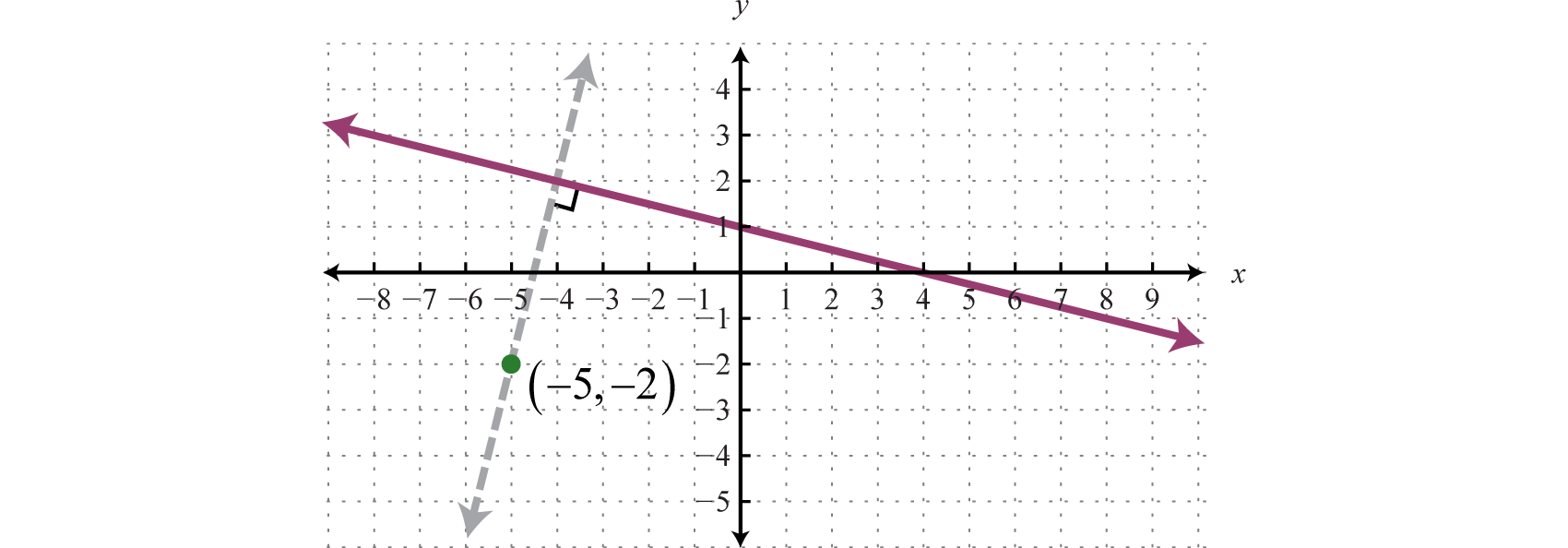
Exercise86
Find an equation of the line passing through \((-5,-2)\) and perpendicular to \(\frac{1}{3}x-\frac{1}{2}y=-2\text{.}\)
SolutionThe equation of the perpendicular line is given by \(y=-\frac{3}{2}x-\frac{19}{2}\text{.}\)
SubsectionElementary Functions
In this section we graph two elementary functions that will be used throughout this course. Each function is graphed by plotting points. For this course \(f(x)=y\) and thus \(f(x)\) and \(y\) can be used interchangeably.
Any function of the form \(f(x)=c\text{,}\) where \(c\) is any real number, is called a constant function. Constant functions are linear and can be written in the form \(f(x)=0x+c\text{.}\) In this form, it is clear that the slope is 0 and the \(y\)-intercept is \((0,c)\text{.}\) Evaluating any value for \(x\text{,}\) such as \(x=2\text{,}\) will result in \(c\text{.}\)
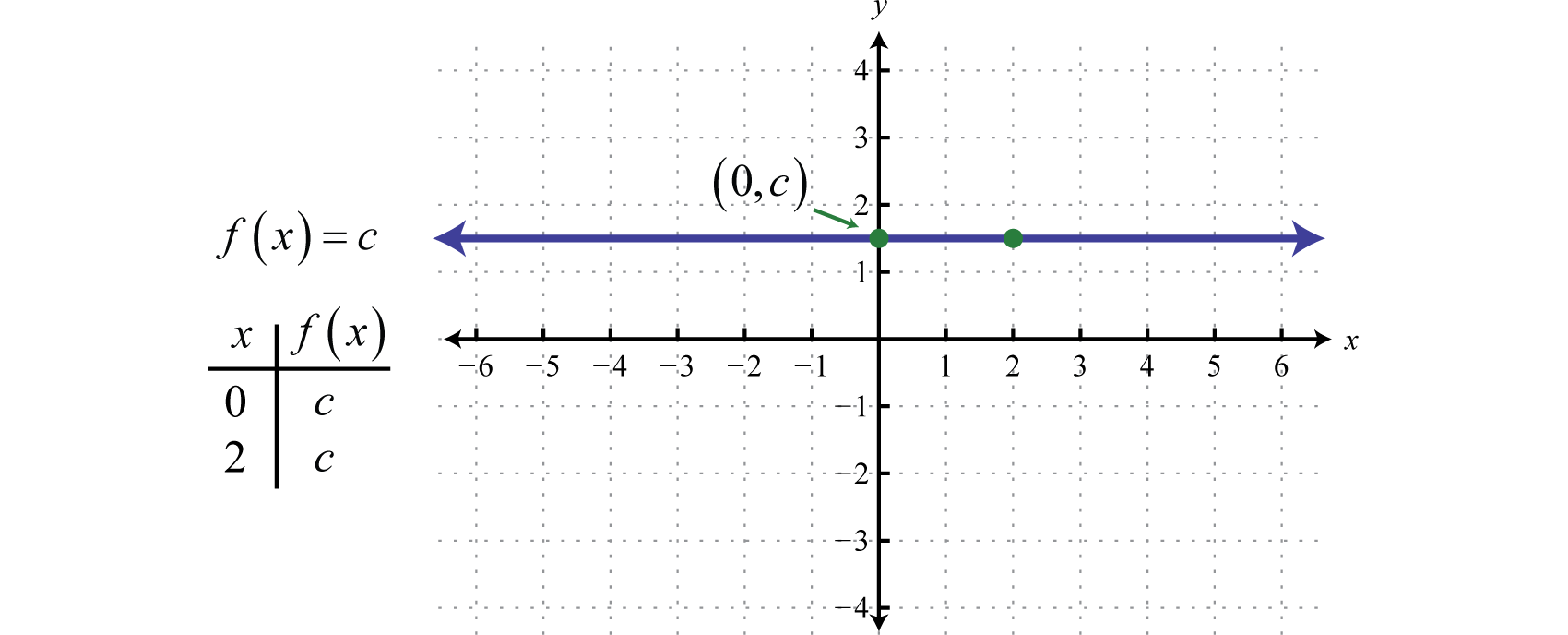
The graph of a constant function is a horizontal line. The domain consists of all real numbers \(\mathbb{R}=(-\infty,\infty)\) and the range consists of the single value \({c}\text{.}\)
We next define the identity function \(f(x)=x\text{.}\) Evaluating any value for \(x\) will result in the same value. For example, \(f(0)=0\) and \(f(2)=2\text{.}\) The identity function is linear, \(f(x)=1x+0\text{,}\) with slope \(m=1\) and \(y\)-intercept \((0,0)\text{.}\)
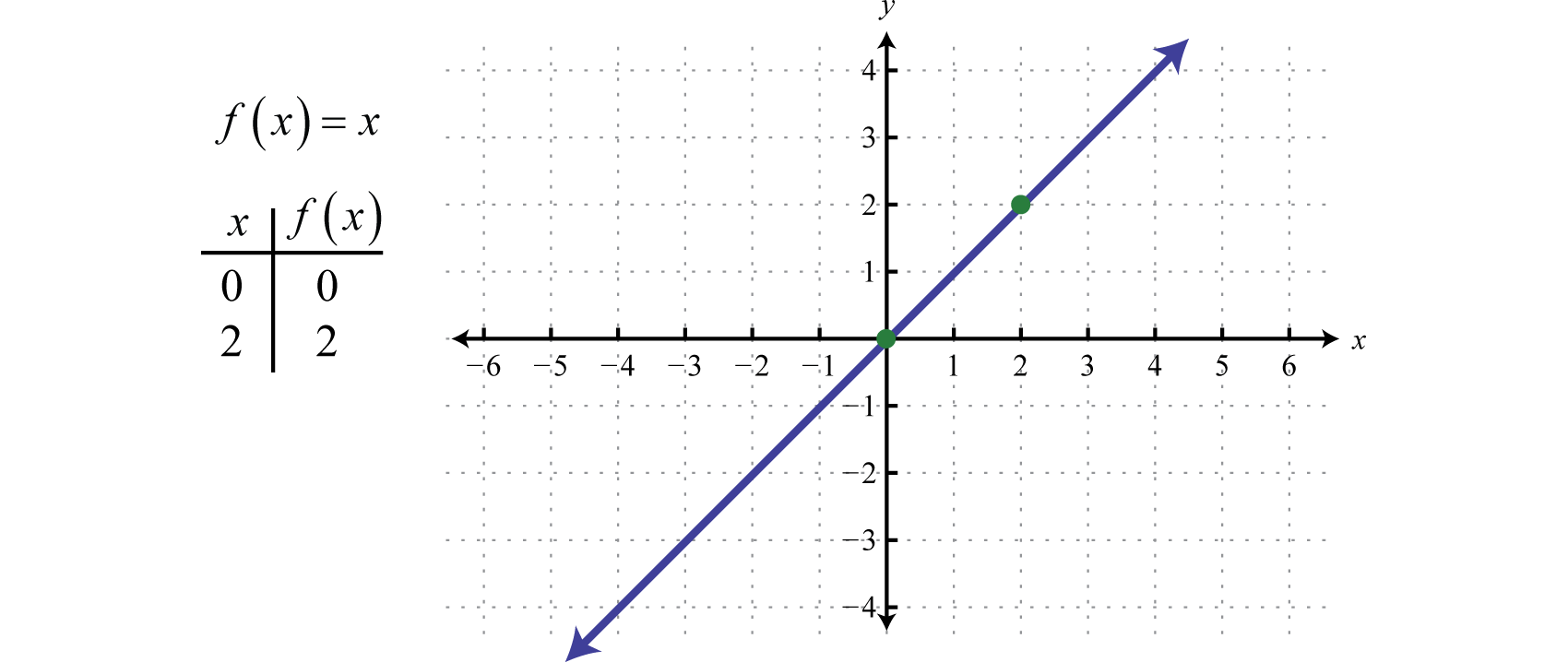
The domain and range both consist of all real numbers, \(\mathbb{R}=(-\infty,\infty)\text{.}\)






