Gerrymandering.
Gerrymandering is the process of manipulating the boundaries of an electoral district using the political affiliation of the constituents to the advantage of those drawing the boundary.
Section 8.2 Gerrymandering
Subsection 8.2.1 Government Representation and Gerrymandering
An important principle in a democracy is the notion of equal representation, in other words every citizen’s vote counts equally. This is the idea behind the way in which people from each state are represented in Congress in the U.S. House of Representatives.
In most states, there are a fixed number of representatives to the state legislature. Rather than apportioning each county a number of representatives, legislative districts are drawn so that each legislator represents a district. To help ensure that citizens are equally represented, each district must include approximately the same number of constituents. Because of this goal, a geographically small city may have several representatives, while a large rural region may be represented by one legislator. Nebraska’s congressional districts, shown in Figure 8.2.1 are a good example of this.
1
images.google.comEvery ten years, the U.S. government conducts a census to measure the U.S. population to determine the number of seats each state has in the U.S. House of Representatives. The census identifies shifts in population and states use this data to redraw district maps. This process is called redistricting and is required by law.
The methods that states use for redistricting vary from state to state. In 37 states, the state legislature draws the districts (usually with some guidance). As a result, the political party that controls the state house also controls the redistricting process. Although the districts are supposed to be roughly equal in population, the configuration of these districts is not clearly prescribed , making the process of redistricting in some states highly politicized. When efforts to redraw the districts are designed to favor one party over another, or one racial group over another, this process is called gerrymandering.
2
Many state constitutions require compactness and contiguity, but no definitions are provided. Nebraska’s state constitution includes these requirements.
3
Eight states use a commission to draw the districts; seven states (Alaska, Delaware, Montana, North Dakota, South Dakota, Vermont, and Wyoming) have only one Congressional district each, so boundaries are not needed.
Example 8.2.2.
Consider three districts which equal population simplified to the three boxes below. On the left there is a college area that typically votes Democratic. On the right is a rural area that typically votes Republican. The rest of the people are more evenly split. The middle district has been voting 50% Democratic and 50% Republican.
As part of redistricting, a Democratic led committee could redraw the boundaries so that the middle district includes less of the typically Republican voters, thereby making it more likely that their party will win in that district, while increasing the Republican majority in the third district.
On the other hand, a Republican led committee might redraw the boundaries to increase rural representation in the middle district while still maintaining a majority in the third district.
There are many methods that politicians use to try to gain an advantage, but the most common are:
- packing— grouping as many members as possible of the opposing party into the smallest number of districts so they win fewer representatives.
- cracking— dividing members of the opposing party into many districts so they will not comprise a majority in very many of them.
Let’s see how this works. Below are three ways to draw five districts (with equal population) to represent 50 people.
4
img.washingtonpost.com/wp-apps/imrs.php?src=https://img.washingtonpost.com/blogs/wonkblog/files/2015/03/gerry.png&w=1484You might notice the unusual shapes used to determine the districts in Method 3. As it turns out, this can often be evidence of gerrymandering. In fact, it is built-in to the origin of the term. In 1812 Elbridge Gerry, the governor of Massachusetts, signed into law a district resembling a salamander (as shown here) designed to favor his party in 1812 elections: Gerry + salamander = gerrymander.
Subsection 8.2.2 Using Mathematics to Combat Gerrymandering
Subsubsection 8.2.2.1 Compactness
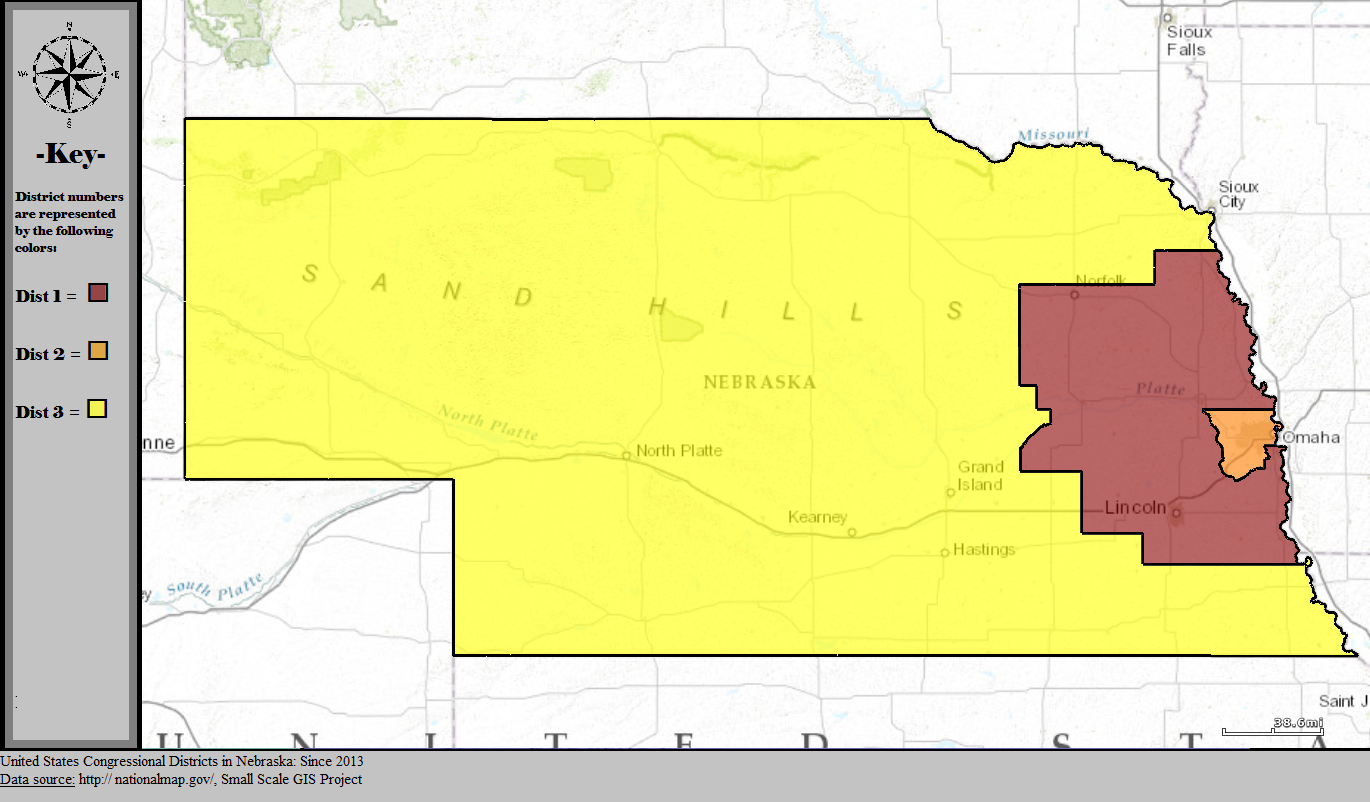
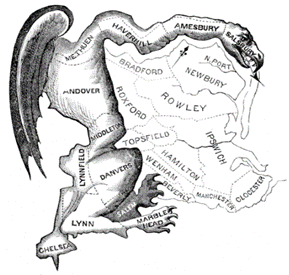
One characteristic which can be described mathematically that is sometimes regarded as an indicator for whether a voting district has been gerrymandered is the notion of compactness. A shape is considered compact when it encloses as much area as possible for a given perimeter.
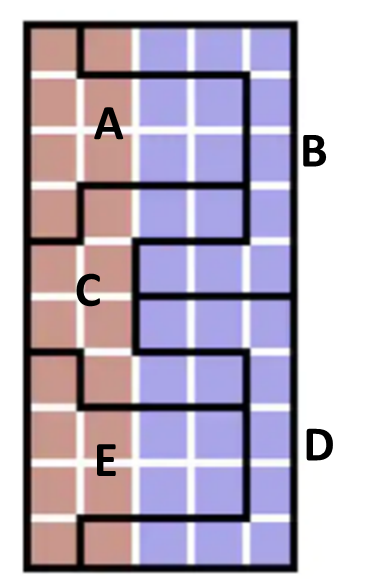
We can recognize shapes that are compact intuitively. For example, we can quickly surmise that the "salamander" shape in the image above is not very compact, while the entire shape (the salamander plus the regions in the image with lighter outlines) is more compact.
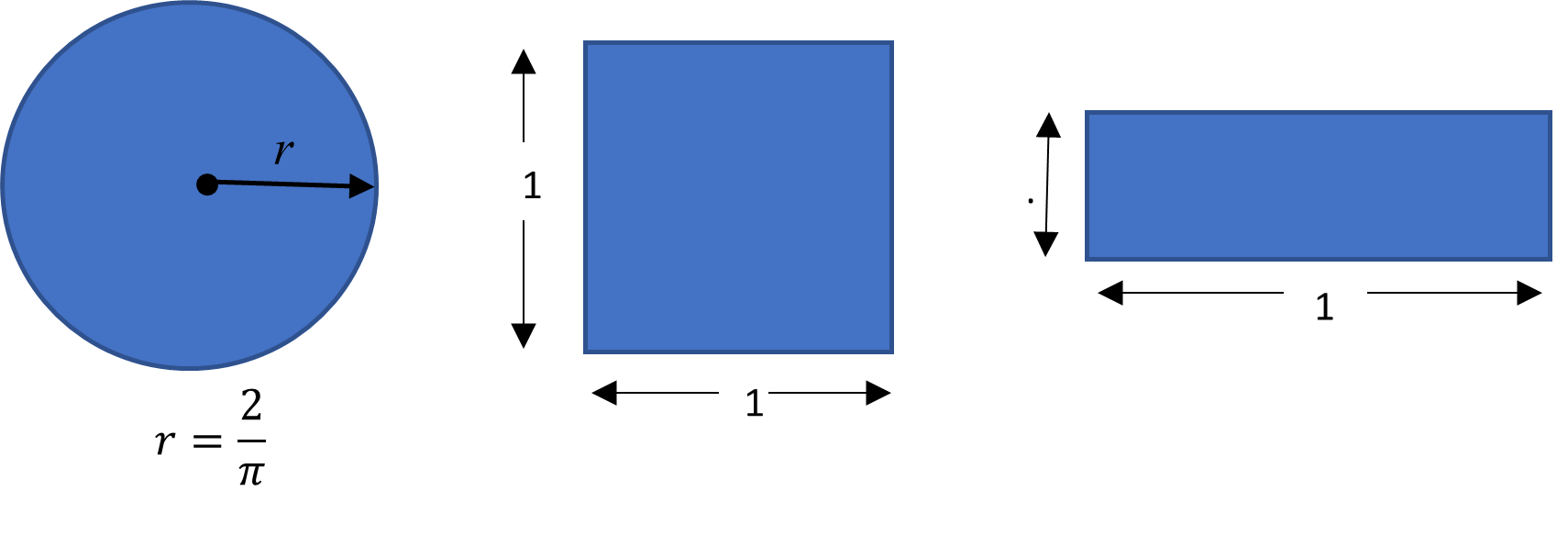
What about other, more familiar two-dimensional geometric shapes? The circle, the square and the rectangle below, are drawn so they all have the same perimeter of approximately 4 units. (Recall that for a circle, the perimeter is called the circumference.)
Can you tell just by looking at them which shape has the greatest area? Let’s check.
| Circle | Square | Rectangle | |
| Perimeter | \(C = 2 \pi r = 4\) | \(P = 1+1+1+1 = 4\) | \(P = 0.5+1.5+0.5+1.5 = 4\) |
| Area (units\(^2\)) | \(A = \pi r^2 = \frac{4}{\pi} \approx 1.27\) | \(A = l \times w = 1 \times 1 = 1\) | \(A = l \times w = 0.5 \times 1.5 = 0.75\) |
If you guessed the circle, you’re correct; the familiar geometric shape that is the most compact is the circle because it has the greatest area for a given perimeter.
As you can see, it is helpful to use numerical values to compare the compactness of a shape. Unfortunately, most of the shapes of voting districts are not going to be this simple. Nevertheless, having a way to quantify the compactness of a voting district is helpful. One way to do this is to use what is known as the Polsby-Popper Score.
Polsby-Popper Score.
The Polsby-Popper Score (PPS) is a measure of the compactness of a voting district given by the formula
\begin{equation*}
\text{PPS} = \frac{4 \pi (\text{Area of District})}{(\text{Perimeter of District})^2}
\end{equation*}
The PPS always falls in the interval [0, 1]. Scores near 0 indicate a lack of compactness, while a score of 1 is the maximum level of compactness.
You might notice the formula involves circles since it includes the number \(\pi\text{.}\) Since circles enclose the most area for a given perimeter, this formula compares the ratio of the area to the perimeter (squared) of any shape to that of a circle, which always has a PPS value of 1.
Example 8.2.4.
Assume the circle, square, and rectangle are voting districts and calculate their PPS scores.
- Circle:\begin{equation*} \text{PPS} = \frac{4 \pi (\text{Area of District})}{(\text{Perimeter of District})^2} = \frac{4 \pi \cdot 1.27}{4^2} = 1 \end{equation*}
- Square:\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 1}{4^2} \approx 0.79 \end{equation*}
- Rectangle:\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 0.75}{4^2} \approx 0.59 \end{equation*}
Example 8.2.5.
Find the PPS of each of the districts in Figure 8.2.3.
- Method 1: All of the districts are the same size. Their perimeter is 22 units and their area is 10 square units. Thus the PPS of each district is given by\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 10}{22^2} \approx 0.26 \end{equation*}
- Method 2: All of the districts are the same size. Their perimeter is 14 units and their area is 10 square units. Thus the PPS of each district is given by\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 10}{14^2} \approx 0.64 \end{equation*}
-
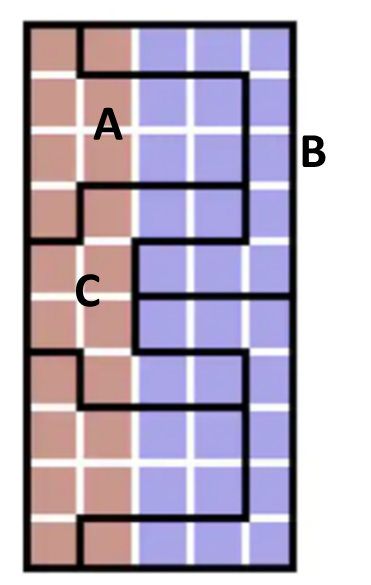
Method 3:
- Shape A:\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 10}{16^2} \approx 0.49 \end{equation*}
- Shape B:\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 10}{22^2} \approx 0.26 \end{equation*}
- Shape C:\begin{equation*} \text{PPS} = \frac{4 \pi \cdot 10}{20^2} \approx 0.31 \end{equation*}
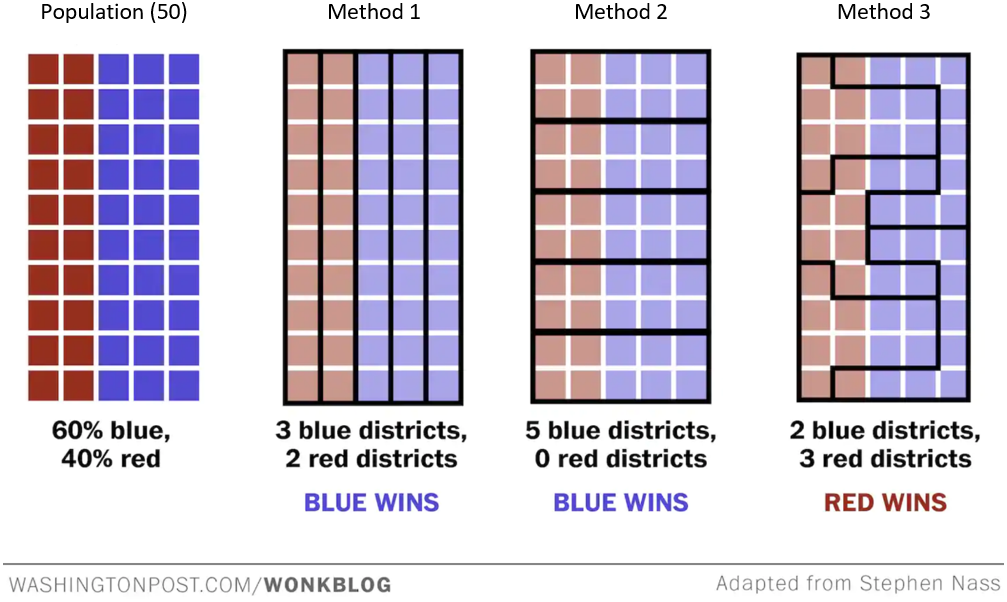
Let’s look again at the districting methods shown in Figure 8.2.3:
Although the PPS of each district is calculated in the previous example, you can tell just by looking at them that the districts in Method 2 are more compact than those in Method 1. Yet the election results of Method 1 are more fair (since they are more aligned with the voting population) than those in Method 2. We see here that although compactness can sometimes be an indicator for whether a district has been gerrymandered, it is not a guarantee. Consequently, we consider another method.
Subsubsection 8.2.2.2 Efficiency Gaps
(Developed by Nicholas Stephanopoulos and Eric McGhee, this method was used in a federal court (Whitford v. Gill, 2016) to declare a legislative map invalid because it evidenced gerrymandering.)
Since shape and compactness are not sufficient for detecting gerrymandering, other methods for quantifying the strategic manipulation of voting districts are needed. Another, more reliable way to measure the degree to which a districting plan is gerrymandered is to compare what we call the efficiency gaps of the parties involved in an election. To learn this method, we first need to think about what it means for a vote to be wasted.
Wasted Votes.
We say votes from a given district can be wasted in two ways:
- If a party wins the district, any votes for that party past the number necessary to win are wasted.
- If a party loses the district, all votes for that party are wasted.
To learn how to identify wasted votes, let’s work an example.
Example 8.2.6.
Find the votes wasted by each party in Method 3 of Figure 8.2.3.
First, we note that there are 10 voters in each district, so 6 are needed to win a district-level election.
- District A: There are exactly 6 red votes. Since all of these are needed to win the election, none of them are wasted. Since Blue lost the election in this district, all 4 blue votes are wasted.
- District B: There are 9 blue votes and 1 red vote. Since only six of them are needed to win, 3 blue votes are wasted. Since Blue won the election, 1 red vote is wasted.
The full list of wasted votes for all of the districting methods in Figure 8.2.3, along with the totals for each district, appear in the table below.
| Wasted votes | District A | District B | District C | District D | District E | Total Wasted |
| Red party | 0 | 1 | 0 | 1 | 0 | 2 |
| Blue party | 4 | 3 | 4 | 3 | 4 | 18 |
We are now ready to define a new measure for detecting gerrymandering.
Efficiency Gap.
The efficiency gap (EG) of a districting plan is a ratio given by the formula
\begin{equation*}
\text{EG} = \frac{|W_A - W_B|}{T}
\end{equation*}
where \(T\) is the total number of votes cast and \(W_A\) and \(W_B\) are the total number of wasted votes for parties A and B, respectively.
If \(0 \leq \text{EG} < 0.07\) (or 7%) the plan is considered fair.
If \(0.07 \leq \text{EG} < 1\) the plan is considered unfair in favor of the party with the least number of wasted votes.
To calculate the Efficiency Gap for Method 3 in Figure 8.2.3, we let A be the red party and B be the blue party and note that the total number of votes cast in the election is \(T = 50\text{.}\) Then we compute the following:
\begin{equation*}
\text{EG} = \frac{|W_A - W_B|}{T} = \frac{|2 - 18|}{50} = \frac{|-16|}{50} = \frac{16}{50} = 0.32
\end{equation*}
Since 0.32 is larger than 0.07, we can conclude that this election is unfair in favor of red (since red had the least number of wasted votes).
Example 8.2.7.
Calculate the efficiency gap EG for districting Method 1 and Method 2 in Figure 8.2.3. Let A be the red voters and B be the blue voters.
- Method 1: Since there are 10 voters in each district, 6 votes are needed to win. In the first two districts, all votes are red, so 4 votes are wasted in each district. In the remaining three districts blue wins, wasting 4 votes per district. Thus, we have\begin{equation*} \text{EG} = \frac{|W_A - W_B|}{T} = \frac{|8 - 12|}{50} = \frac{|-4|}{50} = \frac{4}{50} = 0.08 \end{equation*}Since 0.08 is larger than 0.07, this districting method favors red (but only slightly) since red had the least number of wasted votes.
- Method 2: Each of the districts have the same number of red and blue votes. Since all six blue votes are needed to win the district election, there are zero wasted blue votes. Since blue won each district, all four red votes in each district are wasted, for a total of 20 wasted votes. Thus, we have\begin{equation*} \text{EG} = \frac{|W_A - W_B|}{T} = \frac{|20 - 0|}{50} = \frac{20}{50} = 0.4 \end{equation*}Since 0.4 is larger than 0.07, this districting method significantly favors blue since blue had the least number of wasted votes.
Though the efficiency gap is a better measure of fairness than compactness, it still has weaknesses when being used to detect gerrymandering. Researchers continue to look for ways to monitor the fairness of districting methods in elections.
Subsection 8.2.3 The Impact of Gerrymandering
Both the Republican and Democratic parties have used questionable boundaries to maintain their power. Examples can be used to help illustrate the impact of gerrymandering on the political system.
Example 8.2.8. North Carolina, Congressional District 12.
Even though the population of North Carolina is nearly evenly divided between Republicans and Democrats, at times as many as ten of the thirteen seats in the U.S. House of Representatives for North Carolina have been held by Republicans. This is in large part because of how district lines were drawn when Republicans controlled the redistricting process. In 2016, the Supreme court ruled that the boundary of district 12 (shown below), designed to concentrate the Black vote into one district and limit their influence elsewhere, was deemed unconstitutional. Struggles to ensure that Black and other minority voters have a voice in state elections are ongoing in North Carolina, making District 12 known as "the most gerrymandered district in America".
5
Source: The Guardian
Example 8.2.9. Representation in Massachusetts.
Although nearly one third of the voters in Massachusetts are known to be Republican, since 1994, all nine of their House representatives have been Democrats. Part of the issue in this case, is that the Republican voters are somewhat evenly distributed throughout the state, making it extremely difficult to draw a compact, connected district containing enough Republican voters in any one of them to have a majority. Since Democrats have controlled the redistricting process for nearly three decades, it appears there has been little motivation to make any changes in order to remedy this.
6
Source: Politico
Subsection 8.2.4 Changing the Game
The Voting Rights Act of 1965 created laws which apply to redistricting to prevent states and localities from drawing districts that deny minorities a chance to elect a candidate of their choice. Thus, certain districts are created to contain a majority of minority voters. This requires a balancing act between maintaining a majority of votes and packing too many minorities into a single district. In fact, there are many criteria that states list as important for redistricting and meeting all the criteria is quite difficult. In most cases there is no "best" solution, so the goal is to find a "good" solution. Two examples of this are below.
Example 8.2.10. California, Congressional District 38.
The map to the right shows the 38th congressional district in California in 2014. This district was created through a bi-partisan committee of incumbent legislators. This gerrymandering leads to districts that are not competitive; the prevailing party almost always wins with a large margin.
7
Source: Wikipedia
Example 8.2.11. Illinois, Congressional District 4.
The map to the right shows the 4th congressional district in Illinois in 2004. This district was drawn to contain the two predominantly Hispanic areas of Chicago. The largely Puerto Rican area to the north and the southern Mexican areas are only connected in this districting by a piece of the highway to the west. The result is that voters in this district have typically elected a representative from a minority group, reflecting the diversity of the state; the downside is the large number of wasted votes limits influence outside of these boundaries.
8
Source: Wikipedia
Subsection 8.2.5 The Research Continues
Disputes over district boundaries continue with legislation cases moving back and forth between more and less government intervention, so research about gerrymandering and other policies which result in the underrepresentation of minority groups in government continues. Since their development, both the Polsby-Popper ratio and the efficiency gap, while helpful, have been found to be lacking in their ability to detect unfair practices in voting, increasing the need for better measures. Currently, statistical methods are being studied for determining the fairness of districting plans.
