CC Trigonometric Functions

Section 0.3 Trigonometric Functions

In this chapter we define trigonometric functions. For a more extensive treatment of trigonometric functions we refer the reader to PreCalculus at Nebraska: College Trigonometry

¹³

mathbooks.unl.edu/PreCalculus/part-3.html

Subsection 0.3.1 Periodic Functions

A periodic function is a function whose output values repeat on a regular interval. In mathematical terms, we say that a periodic function is a function for which a specific horizontal shift, \(P\text{,}\) results in the original function: \(f(x+P)=f(x)\) for all values of \(x\text{.}\)

The period of a periodic function is how long it takes for the output values to begin repeating, or the smallest horizontal shift with \(P\gt 0\text{,}\) such that \(f(x+P)=f(x)\) for all values of \(x\text{.}\)

figure showing the period of a periodic function

In addition to the period we also define the midline and amplitude of a periodic function.

The midline of a periodic function is the horizontal line halfway, or midway, between the function’s maximum and minimum output values.

The amplitude of a periodic function is the distance between the function’s maximum (or minimum) output value and the midline.

figure showing midline and amplitude of a periodic function

The midline often represents the average value of a wave-like periodic function and should always be written as the equation of a horizontal line. The amplitude of a periodic function represents how "large" the function’s oscillations are.

Example 0.30.

The London Eye is a huge Ferris wheel in London, England. It completes one full rotation every 30 minutes, and the diameter of its passenger capsules is 130 meters. Riders board the passenger capsules from a platform that is 5 meters above the ground. At time \(t=0\text{,}\) an individual boards the Ferris wheel.

Sketch a graph of \(h=f(t)\text{,}\) where \(h\) is the height of the individual above ground (in meters) after \(t\) minutes.

Solution.

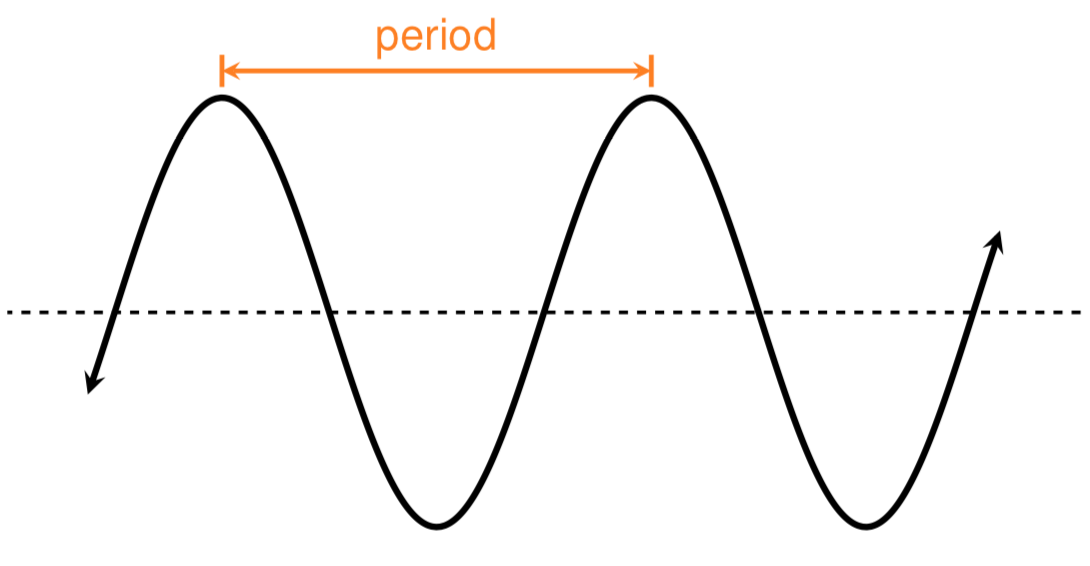
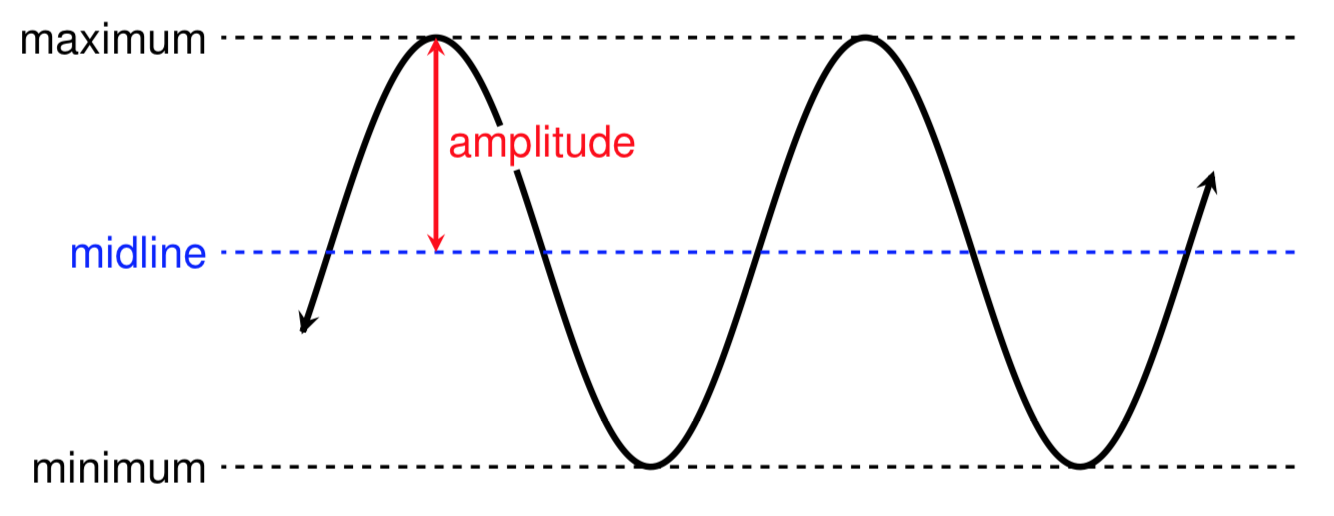
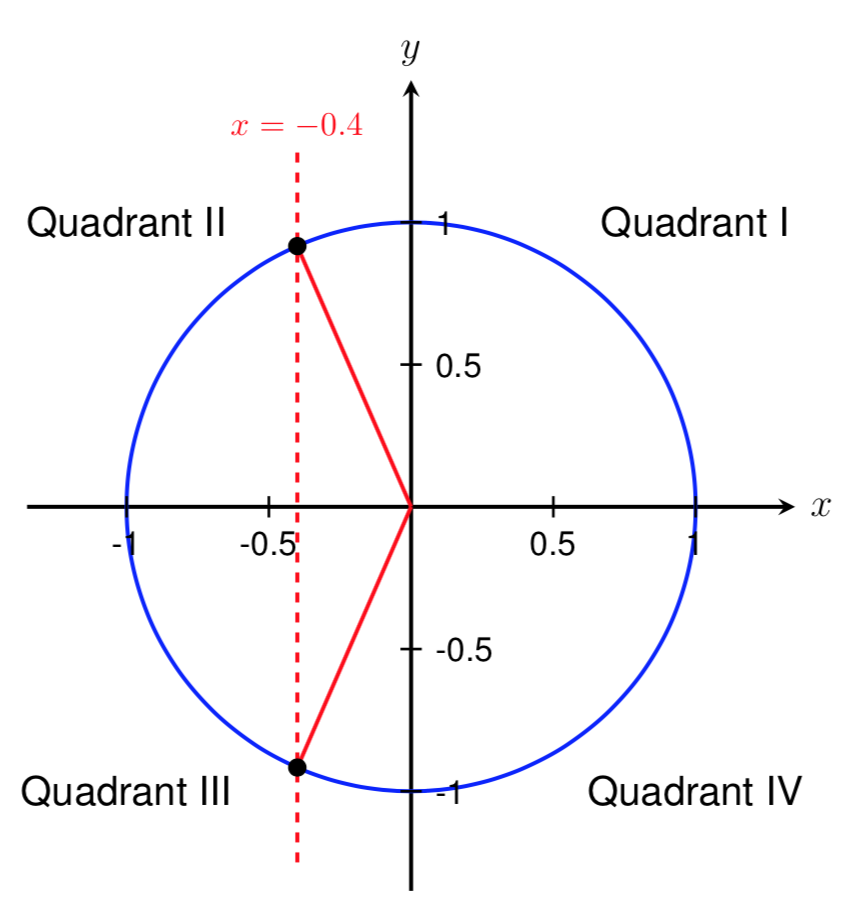
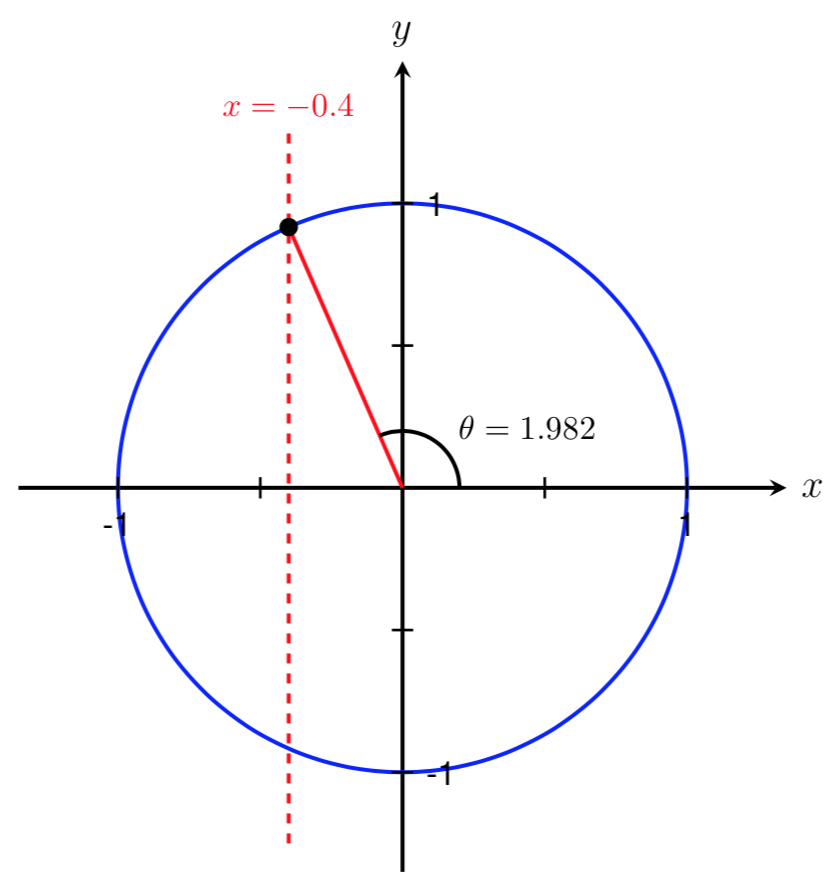
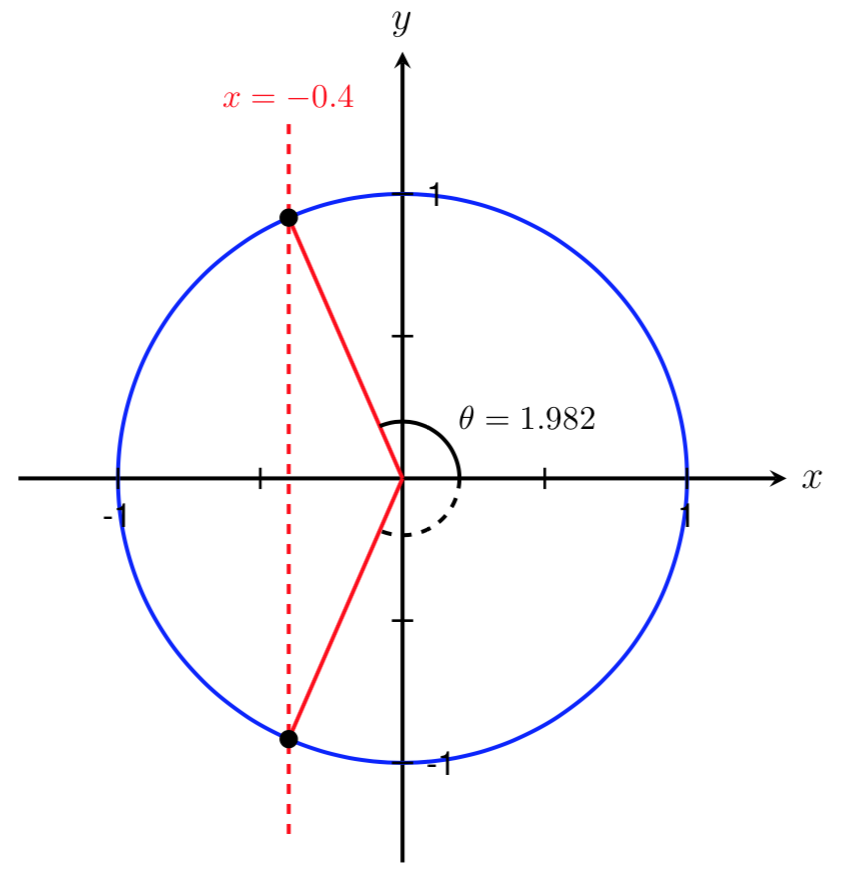
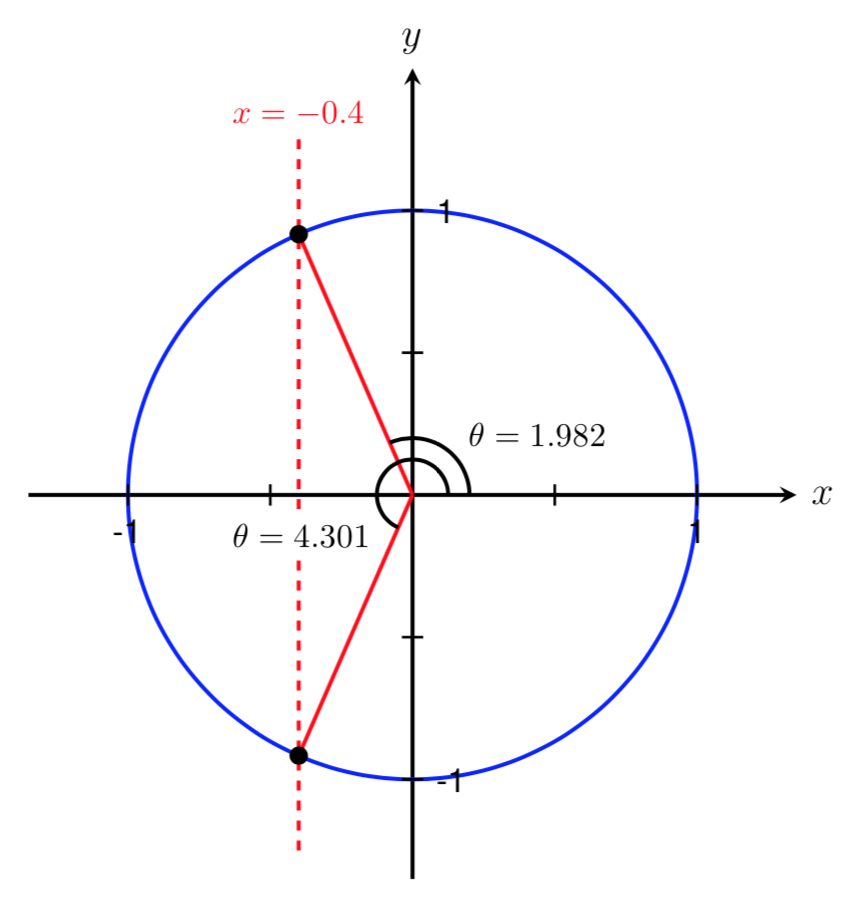
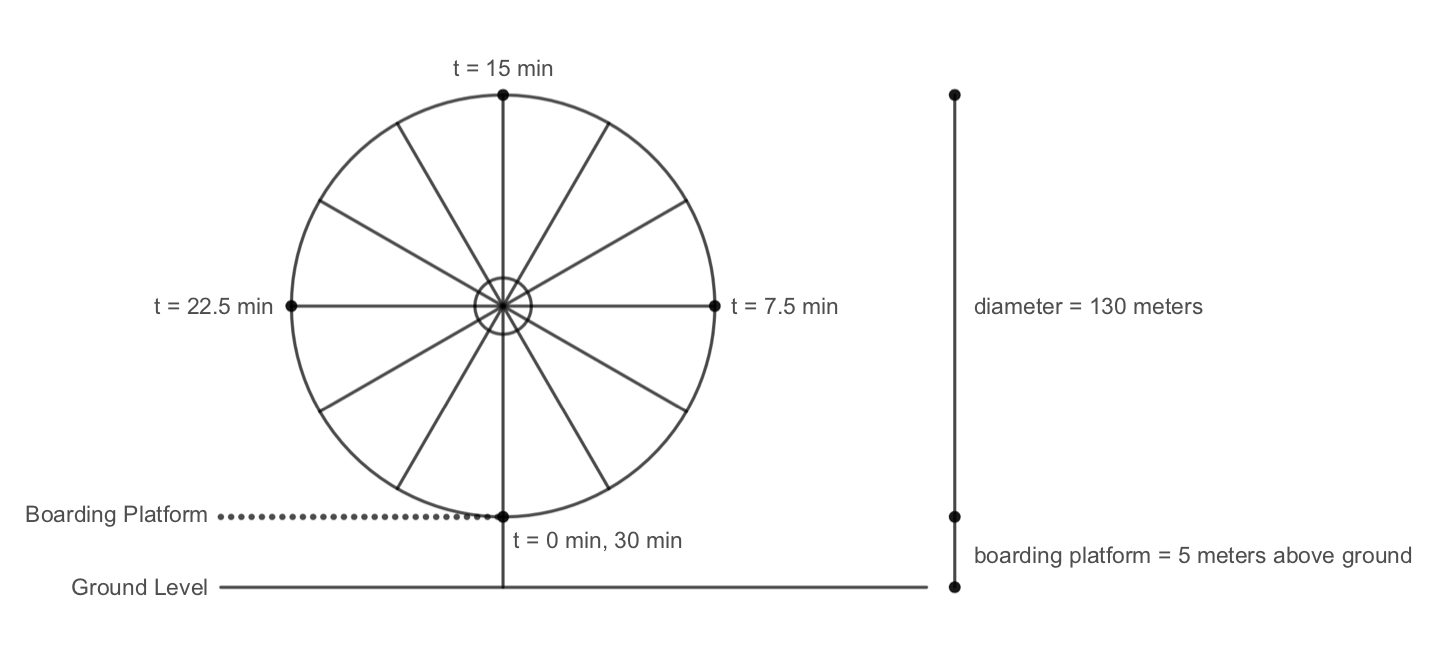
Let’s start by drawing a picture of the Ferris wheel and labeling the known information.

We know that at time \(t=0\) a rider boards the Ferris wheel from the boarding platform, which is 5 meters above the ground. We also know that the Ferris wheel has a diameter of 130 meters and it takes 30 minutes to complete one full revolution around the Ferris wheel.

Since it takes 30 minutes to complete a trip around the Ferris wheel, a rider will reach the top of the Ferris wheel after 15 minutes (assuming that the wheel rotates at a constant speed). Similarly, the rider will reach the three o’clock and nine o’clock positions on the Ferris wheel at 7.5 minutes and 22.5 minutes.

sketch of the London Eye

Next, we can make a table of the rider’s height above ground vs. time.

At time \(t=0\text{,}\) the rider is at the boarding platform, which corresponds to a height of 5 meters above ground. After 15 minutes, the rider reaches the top of the Ferris wheel, which corresponds to a height of 135 meters above ground. We can find this height by taking the height of the boarding platform plus the diameter of the Ferris wheel.

We can also find an intermediate height corresponding to when the rider has been on the Ferris wheel for 7.5 minutes and 22.5 minutes. At these two positions, the rider is halfway between the top of the Ferris wheel and the boarding platform. We can find this height by adding the height of the boarding platform to the radius of the Ferris wheel. Therefore, we get a height of \(5+65 = 70\) meters above ground at these two times.

After 30 minutes, the rider is back at the boarding platform, which corresponds to a height of 5 meters above ground. If the individual were to continue riding the Ferris wheel, this pattern of heights would continue and we could extend our table with additional times and heights as shown below.

time, \(t\) (minutes)	0	7.5	15	22.5	30	37.5	45
height, \(h=f(t)\) (meters)	5	70	135	70	5	70	135

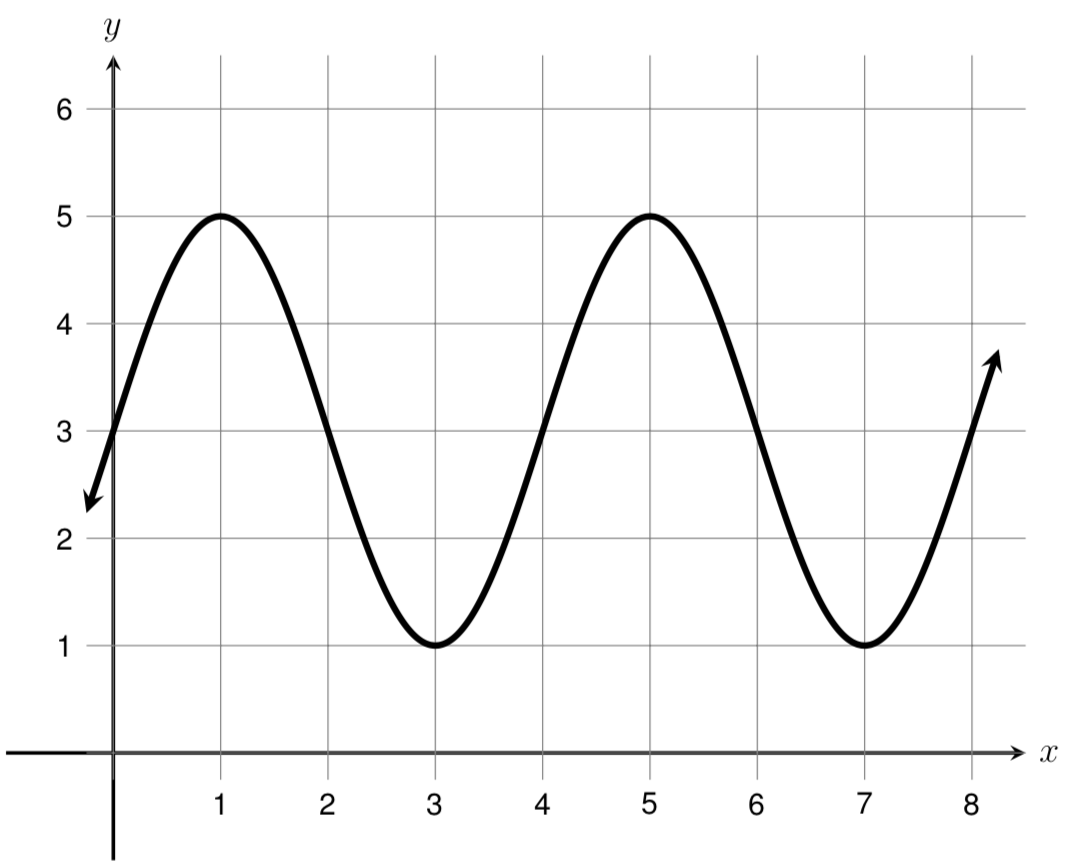
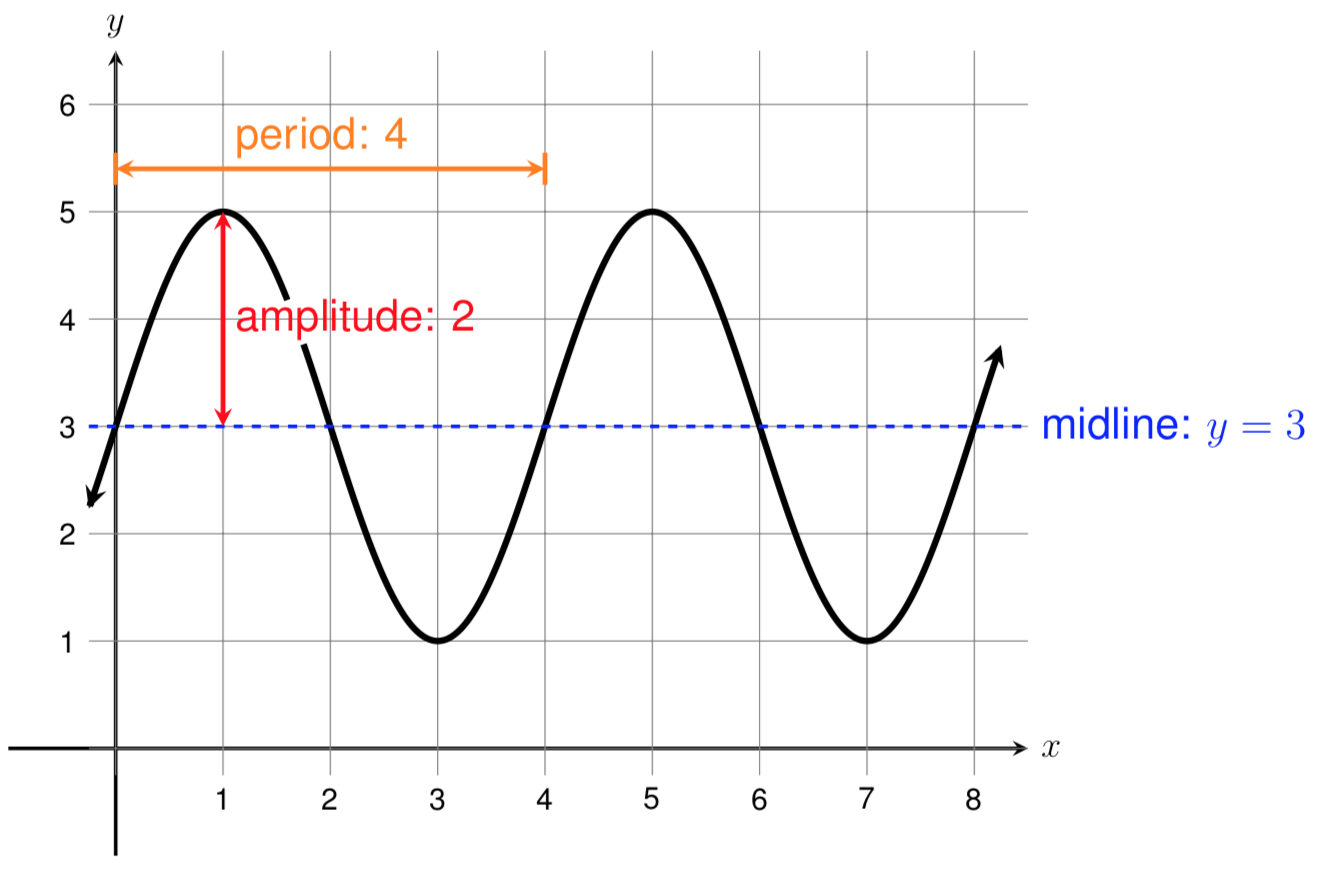
Now that we have a table of times and corresponding heights, we can plot these points and draw a smooth curve between them to create a height vs. time graph.

Since we are graphing height as a function of time, time is our independent variable and should be plotted along the horizontal axis while height is the dependent variable and should be plotted along the vertical axis.

London Eye Graph

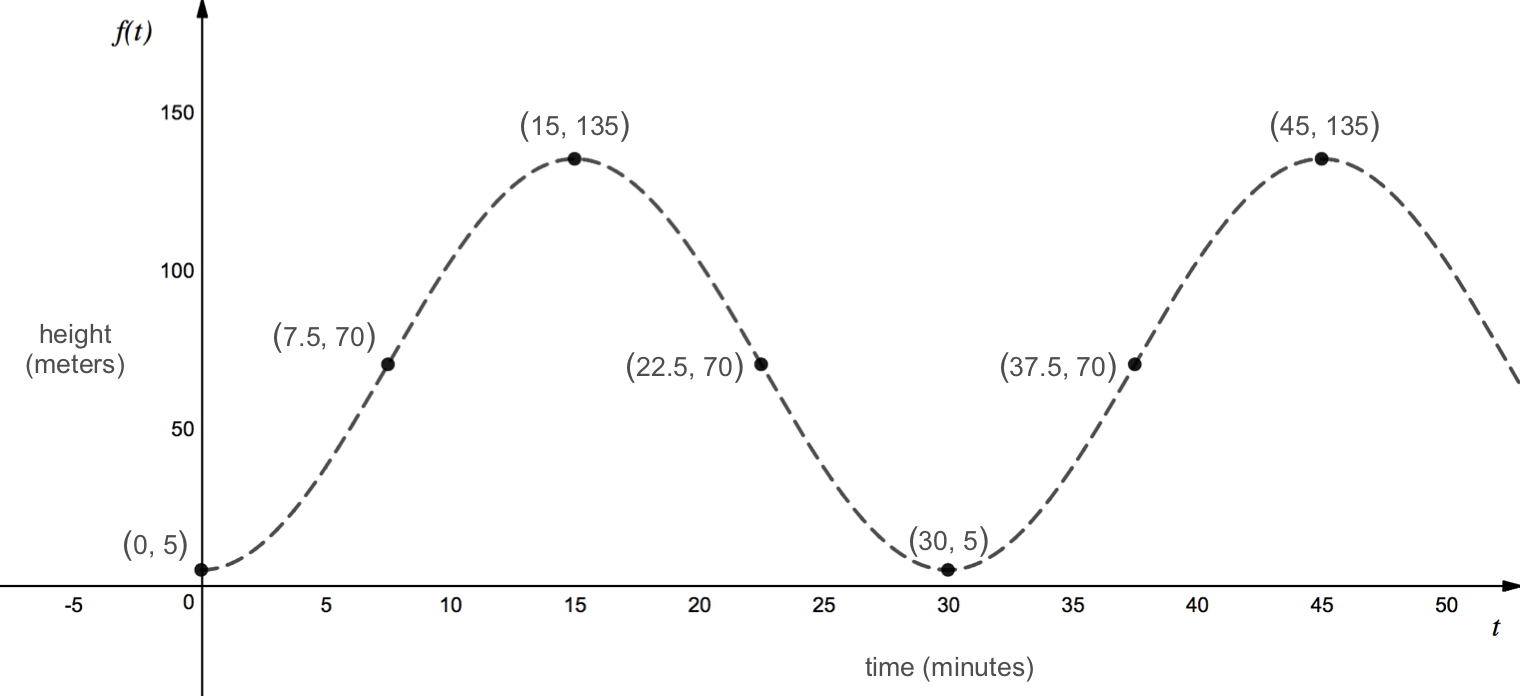
Note that in this example, we assumed that the Ferris wheel was rotating counterclockwise, as shown in our sketch above. For this problem, it did not matter what direction the Ferris wheel was rotating because both clockwise and counterclockwise rotation would have produced the same height vs. time graph. However, this will not always be the case. If the rider were to start in the three o’clock or nine o’clock position, we would need to know whether the Ferris wheel was turning clockwise or counterclockwise in order to sketch a graph of the rider’s height above ground.

Example 0.31.

Find the period, midline, and amplitude of the function shown below.

example for period, midline, and amplitude

Solution.

By definition, the period of the function is how long it takes for the function to start repeating. If we think about the function "starting" at \(x=0\text{,}\) or when it crosses the \(y\)-axis, we can see that it begins repeating when \(x=4\text{.}\) Therefore, the period of the function is 4.

The midline of the function is the horizontal line halfway between the function’s maximum and minimum values. Here, the maximum value of the function is 5 and the minimum value is 1. To find the number halfway between 5 and 1, we can take the average of the two numbers. The average of 5 and 1 is

\begin{equation*} \frac{5+1}{2} = 3 \end{equation*}

Thus, the midline of the function is the line \(y=3\text{.}\)

The amplitude of the function is the distance between the function’s maximum value and the midline. We can find this value by subtracting the midline from the maximum value. Therefore, the amplitude of this function is \(5 - 3 = 2\) .

example solution for period, midline, and amplitude

While measuring angles in degrees may be familiar to many students, doing so often complicates matters since the units of measure can get in the way of calculations. For this reason, another measure of angles is commonly used. This measure is based on the distance around the unit circle.

The Unit Circle.

The unit circle is a circle of radius 1, centered at the origin of the \(xy\)-plane. When measuring an angle around the unit circle, we travel in the counterclockwise direction, starting from the positive \(x\)-axis. A negative angle is measured in the opposite, or clockwise, direction. A complete trip around the unit circle amounts to a total of 360 degrees.

blank unit circle

A radian is a measurement of an angle that arises from looking at angles as a fraction of the circumference of the unit circle. A complete trip around the unit circle amounts to a total of \(2\pi\) radians.

unit circle with 2pi radians labeled

Radians are a unitless measure. Therefore, it is not necessary to write the label "radians" after a radian measure, and if you see an angle that is not labeled with "degrees" or the degree symbol, you should assume that it is a radian measure.

Radians and degrees both measure angles. Thus, it is possible to convert between the two. Since one rotation around the unit circle equals 360 degrees or \(2\pi\) radians, we can use this as a conversion factor.

Converting Between Radians and Degrees.

Since \(360 \text{ degrees} = 2\pi \text{ radians}\text{,}\) we can divide each side by 360 and conclude that

\begin{equation*} \displaystyle 1 \text{ degree} = \frac{2\pi \text{ radians}}{360} = \frac{\pi \text{ radians}}{180} \end{equation*}

So, to convert from degrees to radians, we can multiply by \(\displaystyle \ \frac{\pi \text{ radians}}{180^\circ}\)

Similarly, we can conclude that

\begin{equation*} \displaystyle 1 \text{ radian} = \frac{360^\circ}{2\pi} = \frac{180^\circ}{\pi} \end{equation*}

So, to convert from radians to degrees, we can multiply by \(\displaystyle \ \frac{180^\circ}{\pi \text{ radians}}\)

Example 0.32.

Convert \(\displaystyle \frac{\pi}{6}\) radians to degrees.

Solution.

Since we are given an angle in radians and we want to convert it to degrees, we multiply the angle by \(180^\circ\) and then divide by \(\pi\) radians.

\begin{equation*} \frac{\pi}{6} \text{ radians} \cdot \frac{180^\circ}{\pi \text{ radians}} = 30^\circ \end{equation*}

Example 0.33.

Convert \(15^\circ\) to radians.

Solution.

In this example, we start with an angle in degrees and want to convert it to radians. We multiply by \(\pi\) and divide by \(180^\circ\) so that the units of degrees cancel and we are left with the unitless measure of radians.

\begin{equation*} 15^\circ \cdot \frac{\pi}{180^\circ} = \frac{\pi}{12} \end{equation*}

Subsection 0.3.2 The Common Trigonometric Functions

The Sine and Cosine Functions.

Given an angle \(\theta \ \) (in either degrees or radians) and the \((x,y)\) coordinates of the corresponding point on the unit circle, we define cosine and sine as

\begin{equation*} \cos(\theta)=x \hspace{.25in} \text{and} \hspace{.25in} \sin(\theta)=y \end{equation*}

Note that sine and cosine are functions that take angles as inputs.

unit circle with (x,y) and theta

Using the \((x,y)\) coordinates we can find the cosine and sine values of common angles on the unit circle.

The applet below shows how the graphs of sine and cosine relate to the \(x\) and \(y\) coordinates of the point \(P\) on the unit circle. Move the slider to change the angle \(\theta\) and observe how the \(x\) and \(y\) values of point \(P\) relate to the outputs of \(\cos(\theta)\) and \(\sin(\theta)\text{.}\)

Figure 0.34. How the Graphs of Sine and Cosine Relate to the Unit Circle

The following identity is a consequence of the definitions of sine and cosine on a unit circle and the Pythagorean Theorem.

The Pythagorean Identity.

For any angle \(\theta\text{,}\)

\begin{equation*} \cos^2(\theta)+\sin^2(\theta)=1 \end{equation*}

In addition to sine and cosine it is also useful to define several additional trigonometric functions.

The Tangent Function.

Given an angle \(\theta \ \) (in either degrees or radians) and the \((x,y)\) coordinates of the corresponding point on the unit circle, we define tangent as

\begin{equation*} \tan(\theta)=\frac{y}{x} \end{equation*}

Just like sine and cosine, tangent is a function that takes angles as inputs.

unit circle with (x,y) and theta

Note that since \(\sin(\theta)=y\) and \(\cos(\theta)=x\text{,}\) we can also define tangent as

\begin{equation*} \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)} \end{equation*}

We can find the tangent values of common angles on the unit circle by using the sine and cosine values of the angles (or the corresponding \(y\) and \(x\) coordinates).

So far we have defined cosine, sine, and tangent with the \(x\) and \(y\) coordinates of points on the unit circle. We can also state equivalent, but more general definitions of sine, cosine, and tangent using a right triangle. On the right triangle, we label the hypotenuse as well as the side opposite the angle and the side adjacent (next to) the angle.

Given a right triangle with an angle of \(\theta\text{,}\) we define sine, cosine, and tangent as

\begin{align*} \sin(\theta) \amp =\frac{\text{opposite}}{\text{hypotenuse}} \\ \\ \cos(\theta) \amp =\frac{\text{adjacent}}{\text{hypotenuse}} \\ \\ \tan(\theta) \amp =\frac{\text{opposite}}{\text{adjacent}} \end{align*}

right triangle with labels

A common mnemonic for remembering these relationships is Soh-Cah-Toa formed by the first letters of "Sine is opposite over hypotenuse" and "Cosine is adjacent over hypotenuse." We will return to "Toa" in the next section.

Example 0.35.

Given the triangle shown below, find the value for \(\cos(\theta)\text{,}\) \(\sin(\theta)\text{,}\) and \(\tan(\theta)\text{.}\)

right triangle example

Solution.

The side adjacent to angle \(\theta\) is 15, and the hypotenuse of the triangle is 17. Using the definition of cosine given above, we get that

\begin{equation*} \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{15}{17}. \end{equation*}

The side opposite to angle \(\theta\) is 8, and the hypotenuse of the triangle is 17. Using the definition of sine given above, we get that

\begin{equation*} \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{8}{17}. \end{equation*}

The side opposite to angle \(\theta\) is 8, and side adjacent to angle \(\theta\) is 15. Using the definition of tangent given above, we get that

\begin{equation*} \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{8}{15}. \end{equation*}

Note that we could have also taken

\begin{equation*} \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}=\frac{(\frac{8}{17})}{(\frac{15}{17})}=\frac{8}{15}. \end{equation*}

There are times when it can be useful to consider functions like \(\frac{1}{\sin(\theta)}\) or \(\frac{1}{\cos(\theta)}\text{.}\) This happens often enough that mathematicians have created special names for these types of functions. Generally, these functions are called reciprocal trigonometric functions, and they can be defined in terms of the sine, cosine, and tangent functions.

The Reciprocal Trigonometric Functions.

Given an angle \(\theta\text{,}\) we define:

\begin{align*} \amp \text{the secant function as } \amp\amp \sec(\theta)=\frac{1}{\cos(\theta)}\\ \\ \amp \text{the cosecant function as } \amp\amp \csc(\theta)=\frac{1}{\sin(\theta)}\\ \\ \amp \text{the cotangent function as } \amp\amp \cot(\theta)=\frac{1}{\tan(\theta)} \end{align*}

Example 0.36.

Find \(\sec\left(\frac{5\pi}{6}\right)\text{,}\) \(\csc\left(\frac{5\pi}{6}\right)\text{,}\) and \(\cot\left(\frac{5\pi}{6}\right)\text{.}\)

Solution.

Since \(\frac{5\pi}{6}\) is a common angle on the unit circle, we have that

\begin{align*} \sec\left(\frac{5\pi}{6}\right)\amp=\frac{1}{\cos\left(\frac{5\pi}{6}\right)} = \frac{1}{-\frac{\sqrt{3}}{2}} = -\frac{2}{\sqrt{3}} = -\frac{2\sqrt{3}}{3}\\ \\ \csc\left(\frac{5\pi}{6}\right)\amp=\frac{1}{\sin\left(\frac{5\pi}{6}\right)} = \frac{1}{\frac{1}{2}} = 2\\ \\ \cot\left(\frac{5\pi}{6}\right)\amp=\frac{1}{\tan\left(\frac{5\pi}{6}\right)} = \frac{1}{-\frac{1}{\sqrt{3}}} = -\sqrt{3} \end{align*}

Example 0.37.

Using the triangle shown, evaluate \(\sec(\theta)\text{,}\) \(\csc(\theta)\text{,}\) and \(\cot(\theta)\text{.}\)

triangle for reciprocal trig example

Solution.

To find values for reciprocal trigonometric functions, we must first find values for \(\cos(\theta)\text{,}\) \(\sin(\theta)\text{,}\) and \(\tan(\theta)\text{.}\) We must also find the length of the hypotenuse. Letting the variable \(c\) represent the length of the hypotenuse and using the Pythagorean Theorem, we get that

\begin{align*} c^2 \amp= 8^2 + 15^2 \\ c^2 \amp= 64 + 225 \\ c^2 \amp= 289 \\ c \amp= \pm \sqrt{289} \\ c \amp= 17 \end{align*}

triangle for reciprocal trig example with hypotenuse labeled

Now solving for \(\cos(\theta)\text{,}\) \(\sin(\theta)\text{,}\) and \(\tan(\theta)\text{,}\) we get that

\begin{align*} \cos(\theta) \amp= \frac{15}{17} \\ \\ \sin(\theta) \amp= \frac{8}{17} \\ \\ \tan(\theta) \amp= \frac{8}{15} \end{align*}

Finally, solving for the reciprocal trigonometric functions, we get

\begin{align*} \sec(\theta) \amp= \frac{1}{\cos(\theta)} = \frac{17}{15} \\ \\ \csc(\theta) \amp= \frac{1}{\sin(\theta)} = \frac{17}{8} \\ \\ \cot(\theta) \amp= \frac{1}{\tan(\theta)} = \frac{15}{8} \end{align*}

Subsection 0.3.3 Inverse Trigonometric Functions

In the previous subsection, we evaluated trigonometric functions at various angles, but what do we do if we need to know what angle yields a specific sine, cosine, or tangent value? To find angles, we need inverse trigonometric functions.

Intuitively, if \(\sin(\theta)=a\text{,}\) then \(\arcsin(a)=\theta\text{.}\) However, one must be careful about the domain and range of inverse trig formulas to ensure that they are functions.

The Inverse Sine, Inverse Cosine, and Inverse Tangent Functions.

For \(a\) in \([-1,1] \text{,}\) \(\arcsin(a)\) is defined to be the unique angle \(\theta\) in \([-\frac{\pi}{2},\frac{\pi}{2}]\) for which \(\sin(\theta)=a\) .

For \(a\) in \([-1,1]\text{,}\) \(\arccos(a)\) is defined to be the unique angle \(\theta\) in \([0,\pi]\) for which \(\cos(\theta)=a\text{.}\)

For \(a\) in \((-\infty,\infty)\text{,}\) \(\arctan(a)\) is defined to be the unique angle \(\theta\) in \([-\frac{\pi}{2},\frac{\pi}{2}]\) for which \(\tan(\theta)=a\text{.}\)

Note that the output of each of these inverse functions is an angle .

Remark 0.38.

Do not confuse \(\sin^{-1}(a) \) with \(\frac{1}{\sin(a)}\) as they are not equivalent. The same can be said with \(\cos^{-1}(a) \) and \(\tan^{-1}(a) \text{.}\) As a result, we introduce an alternative (common) notation for the inverse trigonometric functions.

Alternative Notation for the Inverse Sine, Inverse Cosine, and Inverse Tangent Functions.

\(\sin^{-1}(a)=\theta\) is equivalent to \(\arcsin(a)=\theta\)

\(\cos^{-1}(a)=\theta\) is equivalent to \(\arccos(a)=\theta\)

\(\tan^{-1}(a)=\theta\) is equivalent to \(\arctan(a)=\theta\)

Example 0.39.

Find two angles in the interval \([0,2\pi]\) such that \(\displaystyle \sin(\theta)=\frac{1}{2}\text{.}\)

Solution.

Since we are given a sine value, we know that we are looking for angles with a \(y\) coordinate of \(\frac{1}{2}\) on the unit circle.

From the common angles on the unit circle, the two angles where \(\sin(\theta)=\frac{1}{2}\) in the interval \([0,2\pi]\) are

\begin{equation*} \theta = \frac{\pi}{6} \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{5\pi}{6} \end{equation*}

unit circle with sin(theta)=0.5

In the previous example, we were able to use the unit circle to solve for \(\theta\text{,}\) but if we are given trigonometric values that do not correspond to common angles on the unit circle, we will need to use a calculator to find approximate values for \(\theta\) .

Example 0.40.

Find two angles in the interval \([0,2\pi]\) such that \(\cos(\theta)=-0.4\) .

Solution.

Let’s start by drawing a picture and labeling the known information and the angles we are trying to find.

Since we are given a cosine value, we know that we are looking for angles with an \(x\) coordinate of \(-0.4\) on the unit circle. Below is a sketch showing two angles that correspond to \(\cos(\theta) = -0.4\text{.}\) Notice that these two angles lie in Quadrant II and Quadrant III since our cosine value is negative.

unit circle with cos(theta)=-0.4

Since \(x=-0.4\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse cosine function we get that

\begin{equation*} \theta = \cos^{-1}(-0.4) \end{equation*}

To evaluate this, we can use our calculator. Since the output of the inverse function is an angle, our calculator will give us an angle in degrees if it is in degree mode or an angle in radians if it is in radian mode .

Here, we need to decide whether to provide our answer in degrees or radians. Since we are given the interval \([0,2\pi]\text{,}\) which is radians, we will provide our answers in radians. Using our calculator in radian mode we get that

\begin{equation*} \theta \approx 1.982 \text{ radians} \end{equation*}

We have now found one angle in the interval \([0,2\pi]\) such that \(\cos(\theta) = -0.4\text{.}\) However, as shown above, \(\theta\) could lie in either Quadrant II or Quadrant III. Since 1.982 is bigger than \(\frac{\pi}{2} \approx 1.571\) and smaller than \(\pi \approx 3.142\text{,}\) we know that \(\theta=1.982\) lies in Quadrant II. Therefore, we have found the angle shown below.

unit circle with cos(theta)=-0.4 and only one angle shown

We can now use symmetry to find a second angle in the interval \([0,2\pi]\) such that \(\cos(\theta) = -0.4\text{.}\) We know this angle should be located in Quadrant III. By symmetry, we also know that the two angles shown below are equal.

unit circle with cos(theta)=-0.4 and symmetry of two angles shown

Therefore, to find the second angle, we can take the first angle we found and subtract it from \(2\pi\text{.}\) This gives us an angle of

\begin{equation*} \theta \approx 2\pi - 1.982 \approx 4.301 \text{ radians} \end{equation*}

Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\cos(\theta) = -0.4\) are

\begin{equation*} \theta \approx 1.982 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 4.301 \text{ radians} \end{equation*}

unit circle with cos(theta)=-0.4 and two angles labeled

An easy way to check our solutions is to evaluate \(\cos(1.982)\) and \(\cos(4.301)\) on our calculators. If our calculator returns values close to \(-0.4\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get

\begin{equation*} \cos(1.982)=-0.3997 \hspace{.25in} \text{ and } \hspace{.25in} \cos(4.301)=-0.3999 \end{equation*}

Since both of these values are very close and round to -0.4, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\cos(\theta)=-0.4\) .

Example 0.41.

Find all angles in the interval \([0,2\pi]\) such that \(\tan(\theta)=7\text{.}\)

Solution.

Since we are given a tangent value, we know that we are looking for angles where \(\frac{y}{x}=7\) on the unit circle. In addition, our tangent value is positive, so this means that \(\theta\) must lie in Quadrant I, where both \(x\) and \(y\) are positive, or in Quadrant III, where both \(x\) and \(y\) are negative.

Since \(\tan(\theta)=7\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse tangent function we get that

\begin{equation*} \theta = \tan^{-1}(7) \end{equation*}

Using our calculator in radian mode we get that

\begin{equation*} \theta \approx 1.429 \text{ radians} \end{equation*}

We have now found one angle in the interval \([0,2\pi]\) such that \(\tan(\theta) = 7\text{.}\) However, from our work above, we know that \(\theta\) could lie in either Quadrant I or Quadrant III. Since 1.429 is bigger than 0 and smaller than \(\frac{\pi}{2} \approx 1.571\text{,}\) we know that \(\theta=1.429\) lies in Quadrant I. Therefore, we have found the angle shown below.

unit circle with tan(theta)=7 and only one angle shown

We can now use our knowledge of the tangent function to find a second angle in the interval \([0,2\pi]\) such that \(\tan(\theta) = 7\text{.}\) From our work above, we know this angle should be located in Quadrant III, and we also know that the period of tangent is \(\pi\text{.}\) Therefore, the other angle where \(\tan(\theta)=7\) should be located halfway around the unit circle from our first value.

unit circle with tan(theta)=7 and two angles shown

To find this second angle, we can add \(\pi\) to the first angle we found, which gives us an angle of

\begin{equation*} \theta \approx 1.429 + \pi \approx 4.570 \text{ radians} \end{equation*}

Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\tan(\theta) = 7\) are

\begin{equation*} \theta \approx 1.429 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 4.570 \text{ radians} \end{equation*}

unit circle with tan(theta)=7 and two angles labeled

Before we move on, let’s check our solutions by evaluating \(\tan(1.429)\) and \(\tan(4.570)\) on our calculators. If our calculator returns values close to \(7\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get

\begin{equation*} \tan(1.429)=7.005 \hspace{.25in} \text{ and } \hspace{.25in} \tan(4.570)=6.975 \end{equation*}

Since both of these values are very close to 7, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\tan(\theta)=7\text{.}\)

Using inverse trig functions, we can also solve for the angles of a right triangle given two of its sides.

Example 0.42.

Solve the triangle for the angle \(\theta\text{.}\)

right triangle with hypotenuse and adjacent side labeled

Solution.

Since we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.

\begin{align*} \cos(\theta) \amp = \frac{9}{12} \amp\amp\text{Using the definition of the inverse} \\ \\ \theta \amp = \cos^{-1}\left(\frac{9}{12}\right) \amp\amp\text{Evaluating on our calculator} \\ \\ \theta \amp \approx 0.723 \text{ radians} \amp\amp\text{or about } \ 41.410^\circ \end{align*}

right triangle with hypotenuse, adjacent side, and angle labeled

Note 0.43. Common Notation for the Inverse Trigonometric Functions.

The inverse sine function, \(\sin^{-1}(a)\) is sometimes called the arcsine function, and notated \(\arcsin(a)\text{.}\)

The inverse cosine function, \(\cos^{-1}(a)\) is sometimes called the arccosine function, and notated \(\arccos(a)\text{.}\)

The inverse tangent function, \(\tan^{-1}(a)\) is sometimes called the arctangent function, and notated \(\arctan(a)\text{.}\)

Subsection 0.3.4 Generalized Trigonometric Functions

Like all functions, trigonometric functions can be transformed by changing properties like the period, midline, and amplitude of the function. In this subsection, we explore transformations of the sine and cosine functions and use them to model real life situations.

Transformations of Sine and Cosine.

Given an equation in the form

\begin{equation*} f(t) = A\sin(Bt)+k \hspace{.25in} \text{ or } \hspace{.25in} g(t) = A\cos(Bt)+k \end{equation*}

\(|A| \ \) is the vertical stretch/compression and the amplitude of the function.

\(|B| \ \) is the horizontal stretch/compression and is related to the period of the function, \(P\text{,}\) by the formula

\begin{equation*} P=\frac{2\pi}{|B|} \end{equation*}

\(k \ \) is the vertical shift and determines the midline of the function.

Example 0.44.

Sketch a graph of the function

\begin{equation*} g(t)=3\sin(2t)+4 \end{equation*}

Solution.

To begin, let’s find the period, midline, and amplitude of the function.

Using the relationships above, the stretch/compression factor is \(|B|=|2|\text{.}\) Therefore, the period is

\begin{equation*} P = \frac{2\pi}{|B|} = \frac{2\pi}{|2|} = \pi \end{equation*}

The vertical stretch/compression factor is \(|A|=|3|=3\text{,}\) so the amplitude is 3.

Finally, the vertical shift of the function is \(k=4\text{,}\) so the midline of the function is

\begin{equation*} y=4 \end{equation*}

Using our knowledge of the graph of \(f(t)=\sin(t)\text{,}\) we can sketch a transformed graph of \(g(t)=3\sin(2t)+4\text{.}\) Note that the period, midline and amplitude of both functions is different. Thus, the graph of \(g(t)=3\sin(t)+4\) involves a vertical shift up by 4, a vertical stretch of 3, and a horizontal compression by a factor of \(\frac{1}{2}\) from the original graph of \(f(t)=\sin(t)\text{.}\) The graph of \(g(t)=3\sin(2t)+4\) is shown below.

graph of 3sin(2t)+4

Example 0.45.

Determine the midline, amplitude, and period and sketch a graph of the function

\begin{equation*} f(t)=2\cos\left(\frac{\pi}{4}t\right)+1 \end{equation*}

Solution.

To begin, let’s find the period, midline, and amplitude of the function.

Using the relationships above, the stretch/compression factor is \(|B|=|\frac{\pi}{4}|\text{.}\) Therefore, the period of the function is

\begin{equation*} P = \frac{2\pi}{|B|} = \frac{2\pi}{|\pi/4|} = 2\pi \cdot \frac{4}{\pi} = 8 \end{equation*}

The vertical stretch/compression factor is \(|A|=|2|=2\text{,}\) so the amplitude of the function is 2.

Finally, the vertical shift of the function is \(k=1\text{,}\) so the midline of the function is

\begin{equation*} y=1 \end{equation*}

Using our knowledge of the graph of \(g(t)=\cos(t)\text{,}\) we can sketch a transformed graph of

\begin{equation*} f(t)=2\cos\left(\frac{\pi}{4}t\right)+1\text{.} \end{equation*}

Note that the period, midline and amplitude of both functions is different. Thus, the transformed graph involves a vertical shift up by 1, a vertical stretch of 2, and a horizontal stretch by a factor of \(\frac{4}{\pi}\) from the original graph of \(g(t)=\cos(t)\text{.}\) Shown below is the graph of the transformed function

\begin{equation*} f(t)=2\cos\left(\frac{\pi}{4}t\right)+1 \end{equation*}

graph of 2cos(pi/4t)+1

Transforming the amplitude, midline, and period of sinusoidal functions, along with vertical and horizontal reflections, allow us to write equations for a variety of periodic situations.

Example 0.46.

Find a formula for the sinusoidal function graphed below.

graph of -2cos(2pi/5t)+2

Solution.

To begin, let’s find the period, midline, and amplitude of the function graphed above.

Recall that the period of the function is how long it takes for the function to start repeating. If we think about the function "starting" at \(x=0\text{,}\) or when it crosses the \(y\)-axis, we can see that the function above begins repeating when \(x=5\text{.}\) Therefore, the period of the function graphed above is 5.

Since the period of a function is related to \(B\text{,}\) the stretch/compression factor, we can use the relationship \(P = \frac{2\pi}{|B|}\) to solve for \(B\text{.}\) Substituting 5 in for \(P\text{,}\) we get

\begin{align*} 5 \amp= \frac{2\pi}{|B|} \\ \\ |B| \cdot 5 \amp= 2\pi \\ \\ |B| \amp= \frac{2\pi}{5} \end{align*}

For now, we can assume that the \(B\) value is positive, which gives us

\begin{equation*} B = \frac{2\pi}{5} \end{equation*}

The midline of the function is the horizontal line halfway between the function’s maximum and minimum values. Here, the maximum value of the function is 4 and the minimum value is 0. The number halfway between 4 and 0 is 2, so the midline is the line \(y=2\text{.}\) Therefore, the vertical shift of the function graphed above is

\begin{equation*} k=2 \end{equation*}

Finally, the amplitude of the function is the distance between the function’s maximum value and the midline. The distance between the function’s maximum value of 4 and the function’s midline of \(y=2\) is 2, so the amplitude of the function above is 2. Therefore, the vertical stretch factor is

\begin{equation*} |A|=2 \end{equation*}

We now need to decide what type of sinusoidal function to use and whether \(A\) is positive or negative. Note that the function shown above crosses the \(y\)-axis at its minimum value. Therefore, from our work above, we need to use a vertical reflection of a cosine graph to model this function, which means that

\begin{equation*} A=-2 \end{equation*}

Using our work above and substituting our known values into the generalized cosine function \(g(t)=A\cos(Bt) + k\) gives us the following formula for the function graphed above.

\begin{equation*} f(t) = -2\cos\left(\frac{2\pi}{5}t\right) + 2 \end{equation*}

To check our solution, we can use a graphing calculator to graph the function we came up with and confirm that it matches the graph shown above.

Example 0.47.

Find a formula for \(h=f(t)\text{,}\) where \(h\) is the height of the individual above ground (in meters) after \(t\) minutes.

Solution.

Recall that in the London Eye example, we sketched a graph of \(h=f(t)\) for the situation described above. This graph is shown below.

London Eye Graph

Since we have already sketched a graph of this function, we can use this graph to construct a formula for this function.

As shown on the graph, the period of the function is 30 minutes. Therefore, the \(B\) value of the function is

\begin{equation*} |B| = \frac{2\pi}{P} = \frac{2\pi}{30} = \frac{\pi}{15} \end{equation*}

Again, we assume that \(B\) is positive, so

\begin{equation*} B=\frac{\pi}{15} \end{equation*}

The maximum value of the function is 135 meters and the minimum value is 5 meters. The midline is halfway in between these two values and can be found by averaging them:

\begin{equation*} \frac{135+5}{2} = \frac{140}{2} = 70 \text{ meters} \end{equation*}

Thus, the midline of the function is the line \(y=70\) meters, and

\begin{equation*} k=70 \end{equation*}

The amplitude of the function is the distance between the maximum value and the midline which is \(135-70=65\) meters. Therefore,

\begin{equation*} |A|=65 \end{equation*}

Finally, we need to determine what type of function to use and whether the \(A\) value is positive or negative. Since the graph of the function crosses the \(y\)-axis at its minimum value, we can use a negative cosine graph to represent this function. Therefore,

\begin{equation*} A=-65 \end{equation*}

Using our work above and substituting our known values into the generalized cosine function \(g(t)=A\cos(Bt) + k\) gives us the following formula for \(h=f(t)\)

\begin{equation*} f(t) = -65\cos\left(\frac{\pi}{15}t\right) + 70 \end{equation*}

To check our solution, we can use a graphing calculator to graph the function we came up with and confirm that it matches the graph shown above.

Subsection 0.3.5 Supplemental Videos

Periodic Functions
¹⁴
unl.yuja.com/V/Video?v=7114201&node=34303234&a=30576428&autoplay=1
Measuring Angles
¹⁵
unl.yuja.com/V/Video?v=7114199&node=34303309&a=214194212&autoplay=1
Trigonometric and Inverse Trigonometric Functions
¹⁶
unl.yuja.com/V/Video?v=7114202&node=34303285&a=51152015&autoplay=1
Generalized Trigonometric Functions
¹⁷
unl.yuja.com/V/Video?v=7114198&node=34303250&a=167677563&autoplay=1

Exercises 0.3.6 Exercises

1. Period and Amplitude.

Find the period and amplitude of \(r=0.5 \sin(3 t) + 6\)

period =

amplitude =

2. Period and Amplitude.

PTX:ERROR: WeBWorK problem local/setMath106/3-1.pg with seed 15 is either empty or failed to compile Use -a to halt with returned content

3. Finding Trigonometric Functions.

Find the formula for the graph of the function \(f(x)\)given in the graph above.

\(f(x)=\)

4. The Unit Circle.

Consider a circle of radius 8 and a point \(P\) rotating around it, as shown in the figure to the left, below.

The angle \(\theta\text{,}\) in radians, is given as a function of time \(t\text{,}\) by the graph in the second figure.

(a) What is the value of \(\theta\) when \(t=2\text{?}\)

\(\theta=\) .

(b) Find the coordinates of \(P\) when \(t=2\text{.}\)

Coordinates = ( , ).

5. Trigonometric Functions as Compositions.

The following three functions look very similar, but define very different functions. Think about how they are defined and write each as a composition of functions given the information below. (None of the functions in your compositions should be the same as the given function.)

1. \(\tan^{4}(x)=f(g(x))\) where

\(f(x)=\) , and \(g(x)=\) .

2. \(\tan(\tan(x))=f(g(x))\) where

\(f(x)=\) , and \(g(x)=\) .

3. \(\tan x^{4}=f(g(x))\) where

\(f(x)=\) , and \(g(x)=\) .

Prev Top Next