CC Area and Arc Length in Polar Coordinates

Section 6.3 Area and Arc Length in Polar Coordinates

Motivating Questions

How can we compute the area of a sector bounded by a curve?
How can we find the area between two curves?
How can we compute slope and arc length in polar coordinates?

Any point \(P = (x,y) \) on the Cartesian plane can be represented in polar coordinates using its distance from the origin point \((0,0) \) and the angle formed from the positive \(x\)-axis counterclockwise to the point. Sometimes this representation provides a more useful way of describing points and curves than conventional Cartesian coordinates.

Sections Section 6.1 and Section 6.2 were all about computing lengths, areas, and volumes pertaining to curves that were represented in Cartesian coordinates. In this section we’ll examine how these types of computations work in polar coordinates.

Subsection 6.3.1 A Review of Polar Coordinates

Polar Coordinates.

The polar coordinates of a point consist of an ordered pair, \((r,\theta)\text{,}\) where \(r\) is the distance from the point to the origin and \(\theta\) is the angle measured in standard position.

Notice that if we were to “grid” the plane for polar coordinates, it would look like the graph below, with circles at incremental radii and rays drawn at incremental angles.

polar grid

To convert between polar coordinates and Cartesian coordinates, we can use known trigonometric relationships.

Converting Between Polar and Cartesian.

To convert between polar \((r,\theta)\)- and Cartesian \((x,y)\)-coordinates, we can use the following relationships

\begin{align*} \cos(\theta)\amp=\frac{x}{r} \hspace{.6in} x=r\cos(\theta) \\ \\ \sin(\theta)\amp=\frac{y}{r} \hspace{.6in} y=r\sin(\theta) \\ \\ \tan(\theta)\amp=\frac{y}{x} \hspace{.6in} x^2+y^2=r^2 \end{align*}

triangle with \((x,y)\)-coordinates and \((r,\theta)\) labeled

From these relationships and our knowledge of the unit circle, if \(r=1\) and \(\theta=\pi/3\text{,}\) the polar coordinates would be

\begin{equation*} (r,\theta)=\left(1,\frac{\pi}{3}\right) \end{equation*}

and the corresponding Cartesian coordinates would be

\begin{equation*} (x,y)=\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right) \end{equation*}

graph with (r,theta)=(1,\pi/3) labeled

Note 6.34.

Remembering your unit circle values will come in handy as you convert between Cartesian and polar coordinates.

Example 6.35.

Find the Cartesian coordinates of a point with the polar coordinates

\begin{equation*} (r,\theta)=\left(5,\frac{2\pi}{3}\right)\text{.} \end{equation*}

Solution.

Using the above relationships, the \(x\)- and \(y\)-coordinates of the point are

\begin{align*} x \amp= r\cos(\theta) = 5\cos\left(\frac{2\pi}{3}\right)=5\left(-\frac{1}{2}\right)=-\frac{5}{2},\\ \\ y \amp= r\sin(\theta) = 5\sin\left(\frac{2\pi}{3}\right)=5\left(\frac{\sqrt{3}}{2}\right)=\frac{5\sqrt{3}}{2}\text{.} \end{align*}

Thus, the Cartesian coordinates are

\begin{equation*} (x,y)=\left(-\frac{5}{2},\frac{5\sqrt{3}}{2}\right)\text{.} \end{equation*}

Note that since \(2\pi/3\) is a common angle on the unit circle, we can find the exact Cartesian coordinates rather than using a calculator to find approximate values for \(x\) and \(y\text{.}\)

graph with (r,theta)=(5,2pi/3)

Example 6.36.

Find the Cartesian coordinates of a point with the polar coordinates

\begin{equation*} (r, \theta)=(2, \, 4.3)\text{.} \end{equation*}

Solution.

Using the above relationships, the \(x\)- and \(y\)-coordinates of the point are

\begin{equation*} x=r\cos(\theta)=2\cos(4.3) \hspace{.25in} \text{ and } \hspace{.25in} y=r\sin(\theta)=2\sin(4.3)\text{.} \end{equation*}

Since \(\theta=4.3\) radians is not a common angle on the unit circle, we need to use our calculators to find approximate values for \(x\) and \(y\text{.}\) Doing so, we get

\begin{align*} x \amp= 2\cos(4.3) \approx -0.8016,\\ \\ y \amp= 2\sin(4.3) \approx -1.8323\text{.} \end{align*}

Thus, the Cartesian coordinates are

\begin{equation*} (x,y)\approx(-0.8016, -1.8323)\text{.} \end{equation*}

graph with (r,theta)=(2,4.3)

Example 6.37.

Find the polar coordinates of a point with the Cartesian coordinates

\begin{equation*} (x,y)=(3,-4)\text{.} \end{equation*}

Solution.

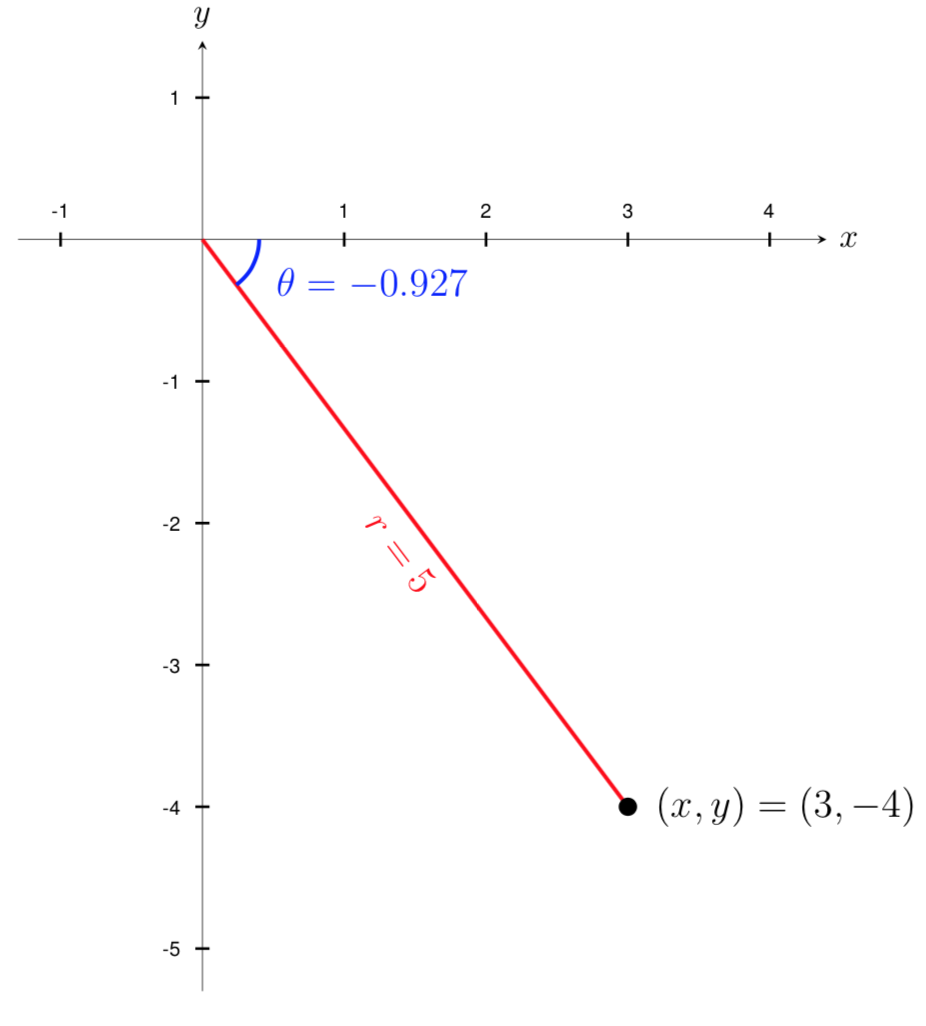
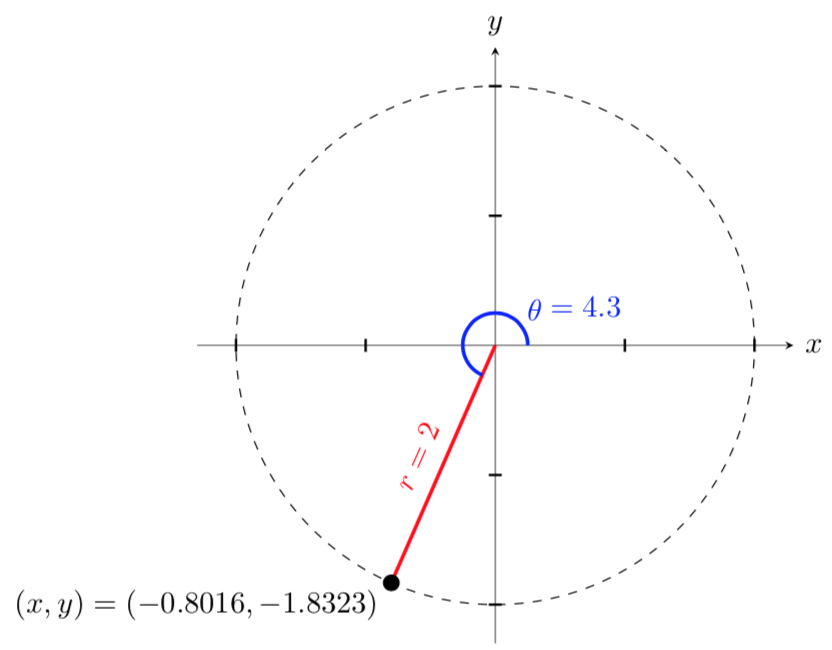
Let’s start by plotting the point \((x,y)=(3,-4)\) on a graph and using the Pythagorean theorem to find the corresponding radius of the point. We get that

\begin{align*} r^2 \amp= x^2 + y^2 \\ \\ r^2 \amp= 3^2 + (-4)^2 \\ \\ r^2 \amp= 9 + 16 \\ \\ r^2 \amp= 25 \\ \\ r \amp= 5 \text{.} \end{align*}

graph with (x,y)=(3,-4)

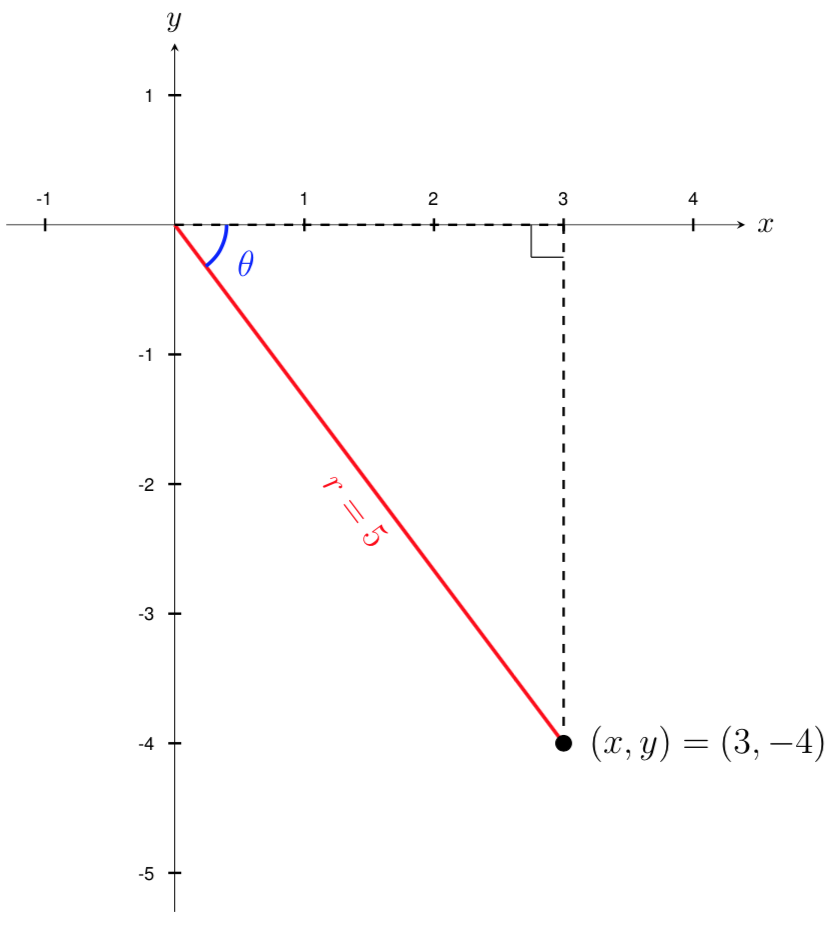
Now that we know the radius, we can find the angle using any of the three trigonometric relationships. Keep in mind that there may be more than one solution when solving for \(\theta\) and we will need to consider the quadrant that our \((x,y)\) point is in to decide which solution to use.

Using the cosine function, we get that

\begin{equation*} \cos(\theta) = \frac{x}{r} = \frac{3}{5} = 0.6\text{.} \end{equation*}

Since this cosine value does not correspond to a common angle on the unit circle, we must use the inverse cosine function to solve for \(\theta\text{,}\) which gives us

\begin{equation*} \theta = \cos^{-1}(0.6) \approx 0.927 \text{ radians}\text{.} \end{equation*}

Since \(0.927\) is greater than 0 and less than \(\pi/2 \approx 1.571\text{,}\) we know that \(\theta=0.927\) lies in Quadrant I. Since the point \((x,y)=(3,-4)\) is located in Quadrant IV, we must find the other angle on the unit circle with \(\cos(\theta) = 0.6\text{.}\)

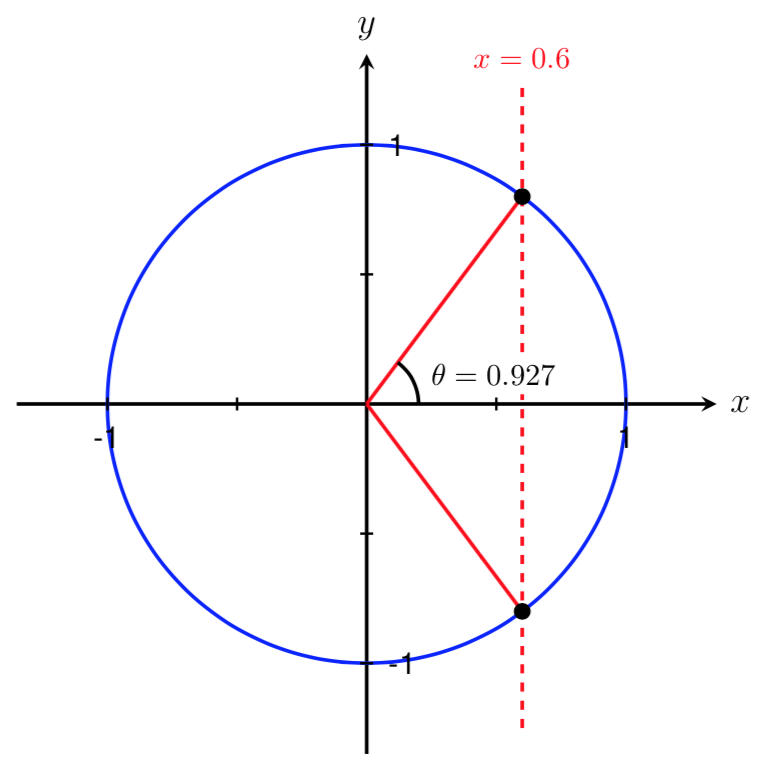
unit circle with cos(\theta)=0.6 one angle shown and labeled

We can use the symmetry of the unit circle to find this second angle. By symmetry, the magnitudes of the two angles shown below are equal. Thus, \(\theta=-0.927\) is another angle that satisfies \(\cos(\theta) = 0.6\text{.}\)

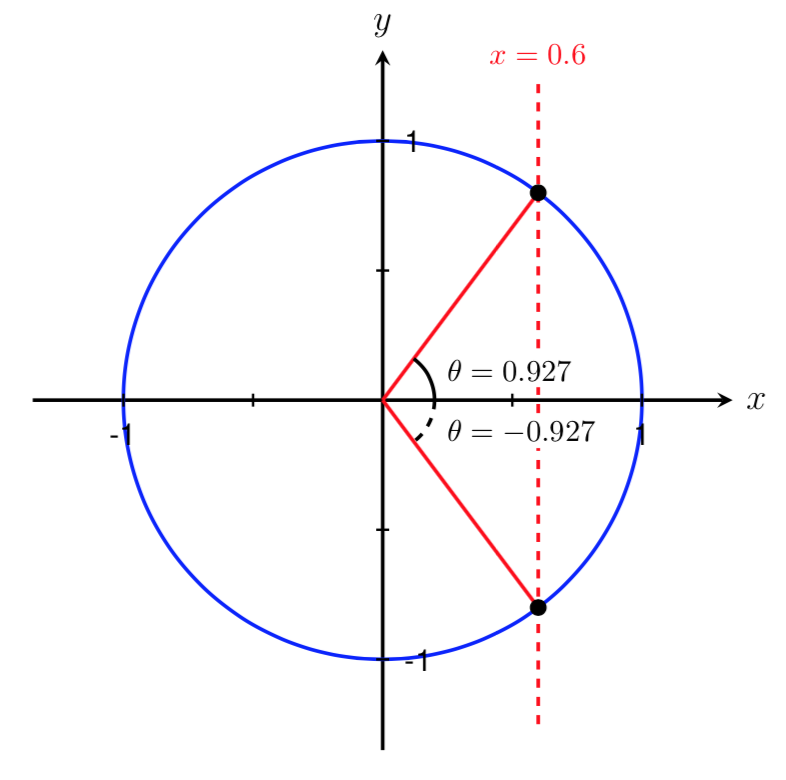
unit circle with cos(\theta)=0.6 two angles shown and labeled

Therefore, the polar coordinates of the point are

\begin{equation*} (r,\theta)=(5, -0.927)\text{.} \end{equation*}

graph with (x,y)=(3,-4)

Example 6.38.

Find the polar coordinates of a point with the Cartesian coordinates

\begin{equation*} (x,y)=\left(-4\sqrt{2},4\sqrt{2}\right)\text{.} \end{equation*}

Solution.

Let’s start by plotting the point \((x,y)=\big(-4\sqrt{2},4\sqrt{2}\big)\) on a graph and using the Pythagorean theorem to find the corresponding radius of the point. We get that

\begin{align*} r^2 \amp= x^2 + y^2 \\ \\ r^2 \amp= \big(-4\sqrt{2}\big)^2 + \big(4\sqrt{2}\big)^2 \\ \\ r^2 \amp= 32 + 32 \\ \\ r^2 \amp= 64 \\ \\ r \amp= 8 \text{.} \end{align*}

graph with (x,y)=(-4sqrt{2},4sqrt{2})

Using the sine function, we get that

\begin{equation*} \sin(\theta) = \frac{y}{r} = \frac{4\sqrt{2}}{8}=\frac{\sqrt{2}}{2}\text{.} \end{equation*}

Since \(y=\sqrt{2}/2\) corresponds to a common angle on the unit circle, we can find an exact value for \(\theta\text{.}\) The two angles that have a sine value of \(\sqrt{2}/2\) on the unit circle are

\begin{equation*} \theta=\frac{\pi}{4} \hspace{.25in} \text{ and } \hspace{.25in} \theta=\frac{3\pi}{4}\text{.} \end{equation*}

Since the point \((x,y)=\big(-4\sqrt{2},4\sqrt{2}\big)\) is located in Quadrant II, we can determine that \(\theta=3\pi/4\text{.}\) Thus, the polar coordinates are

\begin{equation*} (r,\theta)=\left(8, \frac{3\pi}{4}\right)\text{.} \end{equation*}

graph with (x,y)=(-4sqrt{2},4sqrt{2})

Subsection 6.3.2 Examples of Graphs in Polar Coordinates

Any equation written in Cartesian coordinates can be converted to one in polar coordinates and vice-versa. In practice, it makes sense to use the representation that is most natural for the application, or the one which is simpler to express. For example, the unit circle of radius 1 about the origin may be expressed in Cartesian coordinates using the equation

\begin{equation*} x^2 + y^2 = 1. \end{equation*}

Since the points on the circle are precisely those points at distance \(r \) from the origin, in polar coordinates the equation may be written as

\begin{equation*} r = 1. \end{equation*}

Algebraically, we can see that this is correct by substituting \(x = r \cos(\theta) \) and \(y = r \sin(\theta) \) into the original equation to obtain

\begin{equation*} x^2 + y^2 = 1 \end{equation*}

\begin{equation*} r^2 \cos^2(\theta) + r^2 \sin^2(\theta) = 1 \end{equation*}

\begin{equation*} r^2\big( \cos^2(\theta) + \sin^2(\theta) \big) = 1\text{.} \end{equation*}

Using the trig identity \(\cos^2(\theta) + \sin^2(\theta) =1 \text{,}\) this becomes

\begin{equation*} r^2 = 1\text{.} \end{equation*}

Since \(r\) denotes the length of the radius to the point, it follows that \(r\gt0\text{;}\) hence, \(r = 1.\)

We now look at some special families of graphs in polar coordinates.

Example 6.39.

One interesting family of graphs in polar coordinates are the rose graphs. These are curves of the form

\begin{equation*} r = a \cos (n \theta) \end{equation*}

\begin{equation*} r = a \sin (n \theta), \end{equation*}

where \(n \) is a positive integer and \(a \gt 0 \text{.}\)

Figure 6.40. Three rose graphs, \(r=\sin(3\theta)\text{,}\) \(r=\sin(4\theta)\text{,}\) and \(r=\sin(5\theta)\text{.}\)

Now go to this Desmos link

www.desmos.com/calculator/lnuee2xfs4

and make more roses. What changes as you change the value of \(a\text{?}\) The value of \(n\text{?}\)

Solution.

The size of the rose increases directly with \(a\text{.}\) The value of \(n\) changes the number of petals. In particular, if \(n\) is odd, there will be \(n\) petals, and if \(n\) is even, there will be \(2n\) petals.

Example 6.41.

Another noteworthy graph is the Archimedean spiral. This curve has the equation

\begin{equation*} r = \theta \end{equation*}

and is shown below. The general class of spirals is given by the expression

\begin{equation*} r = a + b\theta \end{equation*}

where \(a \gt 0 \text{.}\)

Figure 6.42. Three Archimedean spirals, \(r=\theta\text{,}\) \(r=2\theta+1\text{,}\) and \(r=0.4 \theta+3\text{.}\)

Now go to this Desmos link

www.desmos.com/calculator/vidpkpnryr

and make more spirals. What changes as you change the value of \(b\text{?}\) The value of \(a\text{?}\)

Solution.

The value of \(b\) controls how tight the spiral is. The value of \(a\) controls the “initial radius” of the spiral, namely the value of \(r\) when \(\theta=0\text{.}\)

Subsection 6.3.3 Calculating Area using Polar Coordinates

First consider a circle of radius \(r \) as shown in the image below.

To find the area of a sector with angle \(\theta\text{,}\) we calculate the fraction of the area of the sector compared to the area of the circle. Thus,

\begin{equation*} \text{Area of Sector} = \frac{\theta}{2\pi} (\pi r^2) = \frac{1}{2}r^2 \theta\text{.} \end{equation*}

To find regions of more general shapes, we will consider slicing them into thin regions and approximating the areas of those regions with sectors.

Example 6.43.

Consider the function \(f(\theta)=\cos(2\theta)\) and the region given by the graph of \(r=f(\theta)\) on the interval \(0 \leq \theta \leq 2 \pi\) (shown below).

How would we approximate the area of this region? Our normal strategy would be to cut the region into rectangles and take a Riemann sum of the areas of those rectangles, but because we are working in polar coordinates, it is more natural to approximate the region with the sectors of a circle. One such sector is drawn on the image. That sector has an angle of \(\Delta \theta\) and a radius of \(f(\theta_i)\text{,}\) so

\begin{equation*} \text{area}_{\text{slice}} \approx \text{area}_{\text{sector}}= \frac 12 (f(\theta_i))^2 \Delta \theta\text{.} \end{equation*}

Taking the Riemann sum and taking the limit as \(\Delta \theta \rightarrow 0 \text{,}\) we get that the area of the region is given by the integral \(\int_\alpha^\beta \frac 12 (f(\theta))^2 \, d \theta \text{.}\)

For this particular function, the area contained by \(r=f(\theta)\) on the interval \(0\le\theta\le2\pi\) is thus

\begin{equation*} \int^{2\pi}_0\frac12\cos^2(2\theta)\,d\theta=\frac{\pi}2\text{.} \end{equation*}

We summarize our finding here:

Area in Polar Coordinates.

For a curve \(r = f(\theta) \) where \(f(\theta) \ge 0 \text{,}\) the area between the origin and the curve \(f(\theta) \) from \(\alpha\) to \(\beta \) is

\begin{equation*} \text{Area} = \frac{1}{2} \int_{\theta=\alpha}^{\theta=\beta} f(\theta)^2 \ d\theta\text{.} \end{equation*}

Example 6.44.

Consider the Archimedean spiral given by \(r=\theta\text{.}\) Find the area traced out in the first loop of the spiral (from \(\theta=0\) to \(\theta=2\pi\)).

Hint.

Apply the formula in “Area in Polar Coordinates”.

Answer.

\(A=\frac{4}{3} \pi^3 \text{.}\)

Solution.

Since \(r=f(\theta)=\theta\text{,}\) then by the "Area in Polar Coordinates" formula,

\begin{align*} A\amp= \frac 12 \int_{\theta=0}^{\theta=2\pi}\theta^2 \, d \theta \\ \amp=\left. \frac 16 \theta^3 \right |_{\theta=0}^{\theta=2\pi}\\ \amp= \frac{4}{3} \pi^3 \text{.} \end{align*}

Example 6.45.

Consider the rose given by \(r=\sin(4\theta)\text{.}\) Find the area traced out by the rose (the entire rose is traced out from \(\theta=0\) to \(\theta=2\pi\)).

Hint.

Apply the formula in “Area in Polar Coordinates” and the trig identity \(\sin^2(x)=\frac 1 2 - \frac 1 2 \cos(2x)\text{.}\)

Answer.

\(A= \frac \pi 2 \text{.}\)

Solution.

Since \(r=f(\theta)=\sin(4\theta)\text{,}\) then by the "Area in Polar Coordinates" formula,

\begin{align*} A\amp= \frac 12 \int_{\theta=0}^{\theta=2\pi}\big(\sin(4\theta)\big)^2 \, d \theta\\ \amp= \frac 12 \int_{\theta=0}^{\theta=2\pi}\left(\frac 1 2 -\frac 1 2\cos (8 \theta)\right) \, d \theta \\ \amp=\left. \frac 12 \left(\frac 1 2\theta - \frac 1 {16} \sin(8 \theta)\right) \right |_{\theta=0}^{\theta=2\pi}\\ \amp= \frac \pi 2 \text{.} \end{align*}

Example 6.46.

Let \(f(\theta)=\theta\) and \(g(\theta)=\pi-\theta\text{,}\) and consider the shark-fin shaped region traced out by the two Archimedean spirals \(r=f(\theta)\) and \(r=g(\theta)\) and the \(x\)-axis (shown below).

Find the \((r,\theta)\)- and \((x,y)\)-coordinates of the point where the curves meet.
In Section 6.1, we approximated areas by taking either vertical or horizontal rectangles whose two ends were on different curves bounding the region. Would that method work to find the area of the shark-fin region? If so, set up and evaluate the integrals. If not, explain why not.
In order to find the area of the shark fin, we will first find two other areas, then combine our answers. Set up and evaluate an integral that gives the area of the region bounded by \(r=f(\theta)\) and the \(y\)-axis.
In order to find the area of the shark fin, we will first find two other areas, then combine our answers. Set up and evaluate an integral that gives the area of the region bounded by \(r=g(\theta)\text{,}\) the \(y\)-axis, and the \(x\)-axis.
Combine your answers to the previous parts to find the area of the shark-fin shaped region.

Hint.

Solve the equation \(f(\theta)=r=g(\theta)\text{.}\)
Neither vertical nor horizontal rectangles would produce an easy integral.
Apply the formula in “Area in Polar Coordinates”.
Apply the formula in “Area in Polar Coordinates”.
How can you combine the regions in parts (c) and (d) to make the shark-fin shaped region?

Answer.

\((r,\theta)=\big(\frac \pi 2,\frac \pi 2\big)\text{.}\) \((x,y)=\big(0, \frac \pi 2\big)\text{.}\)
Neither vertical nor horizontal rectangles would produce an easy integral.
\(A=\frac{\pi^3}{48} \text{.}\)
\(A=\frac{7\pi^3}{48} \text{.}\)
\(A=\frac{\pi^3}{8} \text{.}\)

Solution.

The curves meet when \(f(\theta)=r=g(\theta)\text{,}\) so when \(\theta=\pi-\theta\text{,}\) which is at \(\theta=\frac \pi 2\text{.}\) Plugging back into \(f(\theta)\) or \(g(\theta)\) gives that \(r= \frac \pi 2\text{.}\) Thus the \((r,\theta)\)-coordinates are \(\big(\frac \pi 2,\frac \pi 2\big)\text{.}\)

The \((x,y)\)-coordinates can be found by \(x=r \cos(\theta)\text{,}\) \(y=r \sin(\theta)\text{,}\) so \((x,y)=\big(0, \frac \pi 2\big)\text{.}\)
Neither vertical nor horizontal rectangles would produce an easy integral. For vertical rectangles, near the \(y\)-axis, both ends of the rectangles would be on the curve \(r=f(\theta)\text{,}\) which would make the integral hard to set up and evaluate. For horizontal rectangles, near the top of the region, both ends of the rectangles would be on the curve \(r=g(\theta)\text{,}\) which would make the integral hard to set up and evaluate.
This region goes from \(\theta=0\) to \(\theta= \frac \pi 2\text{,}\) so its area is given by

\begin{align*} A\amp= \frac 1 2 \int_0^{\frac \pi 2} (f(\theta))^2 \, d \theta \\ \amp= \frac 1 2 \int_0^{\frac \pi 2} \theta^2 \, d \theta \\ \amp= \left. \frac 1 6 \theta^3 \right|_0^{\frac \pi 2} \\ \amp=\frac{\pi^3}{48}\text{.} \end{align*}
This region goes from \(\theta=0\) to \(\theta= \frac \pi 2\text{,}\) so its area is given by

\begin{align*} A\amp= \frac 1 2 \int_0^{\frac \pi 2} (g(\theta))^2 \, d \theta \\ \amp= \frac 1 2 \int_0^{\frac \pi 2} (\pi-\theta)^2 \, d \theta \\ \amp= \left. \frac {-1} 6 (\pi-\theta)^3 \right|_0^{\frac \pi 2} \\ \amp= \left(\frac{-\pi}{48}\right)+ \frac{\pi^3}{6}\\ \amp=\frac{7\pi^3}{48}\text{.} \end{align*}
The shark-fin shaped region is made from the region in (d) minus the region in (c), so its area is

\begin{equation*} A= \frac{7\pi^3}{48}-\frac{\pi^3}{48}= \frac{\pi^3}{8}\text{.} \end{equation*}

Subsection 6.3.4 Slope and Arc Length with Polar Coordinates

We can think of a curve \(r = f(\theta) \) in terms of \(x \) and \(y\) by using \(x = r \cos(\theta) \) and \(y = r\sin(\theta) \text{.}\) In this way, the curve may be seen as being parametrized by \(\theta \text{.}\) Thus, we may use the formulas for slope and arc length of parametric equations to obtain formulas for slope and arc length in polar coordinates.

Slope in Polar Coordinates.

The slope of a curve \(r = f(\theta) \) is

\begin{equation*} \frac{dy}{dx} = \frac{\big(\frac{dy}{d\theta}\big)}{\big(\frac{dx}{d\theta}\big)}\text{.} \end{equation*}

Arc Length in Polar Coordinates.

The arc length of the curve \(r = f(\theta) \text{,}\) where \(x = r \cos(\theta) \) and \(y = r\sin(\theta) \text{,}\) is

\begin{equation*} \text{Arc Length} = \int_{\theta=\alpha}^{\theta=\beta} \sqrt{\left(\frac{dx}{d \theta} \right)^2 + \left(\frac{dy}{d \theta}\right)^2 } \, d\theta\text{.} \end{equation*}

Example 6.47.

Let \(f(\theta)=2\theta+3\text{,}\) and consider the Archimedean spiral given by the equation \(r=f(\theta)\) for \(0 \leq \theta \leq 2 \pi\text{.}\) The spiral is shown below.

The point labelled "A" is at \(\theta=3 \pi/4\text{.}\) Find the \((x,y)\)-coordinates of A and the slope of the tangent line there.
The point labelled "B" is at \(\theta=7 \pi/4\text{.}\) Find the \((x,y)\)-coordinates of B and the slope of the tangent line there.
Find the length of the piece of the spiral in the third quadrant. (You may wish to use a computer or calculator to numerically evaluate the integral.)

Hint.

You will need to evaluate \(\frac{dx}{d\theta}\) and \(\frac{dy}{d\theta}\) at \(A\text{.}\)
You will need to evaluate \(\frac{dx}{d\theta}\) and \(\frac{dy}{d\theta}\) at \(B\text{.}\)
Find \(\frac{dx}{d\theta}\) and \(\frac{dy}{d\theta}\) and use the arc length formula in "Arc Length in Polar Coordinates".

Answer.

\(\frac{dy}{dx} \approx 0.588 \text{.}\)
\(\frac{dy}{dx} \approx 0.7499 \text{.}\)
Arc Length \(\approx 17.33 \text{.}\)

Solution.

Since \(r=2 \theta+3\text{,}\) \(x=r \cos(\theta)\text{,}\) and \(y=r \sin(\theta)\text{,}\) and \(\theta=\frac{3\pi}4\) at A, then

\begin{equation*} r=\frac{3 \pi}{2}+3,\\ x= \left(\frac{3 \pi}{2}+3 \right)\left(-\frac{\sqrt 2}2\right) \approx -5.45, \text{ and}\\ y= \left(\frac{3 \pi}{2}+3 \right)\left(\frac{\sqrt 2}2\right) \approx 5.45\text{.} \end{equation*}

Now to find \(\frac{dy}{dx}\) we write

\begin{equation*} x= r \cos(\theta)=(2 \theta+3) \cos(\theta)\\ y= r \sin(\theta)=(2 \theta+3) \sin(\theta). \end{equation*}

Thus, taking \(\frac{d}{d\theta}[x]\) and \(\frac{d}{d\theta}[y]\) and applying the product rule, we get

\begin{equation*} \frac{dx}{d\theta} = 2\cos(\theta)+ (2 \theta +3)(-\sin(\theta))\\ \frac{dy}{d\theta} = 2\sin(\theta)+ (2 \theta +3)(\cos(\theta))\text{.} \end{equation*}

Finally, plugging in \(\theta= \frac{3 \pi}{4}\) gives

\begin{align*} \frac{dy}{dx}= \frac{\left(\frac{dy}{d\theta}\right)}{\left(\frac{dx}{d\theta}\right)} \amp= \frac{2\sin(\theta)+ (2 \theta +3)(\cos(\theta))}{2\cos(\theta)+ (2 \theta +3)(-\sin(\theta))}\\ \amp\approx 0.588\text{.} \end{align*}
Since \(r=2 \theta+3\text{,}\) \(x=r \cos(\theta)\text{,}\) and \(y=r \sin(\theta)\text{,}\) and \(\theta=\frac{7\pi}4\) at B, then

\begin{equation*} r=\frac{7 \pi}{2}+3,\\ x= \left(\frac{7 \pi}{2}+3 \right)(\frac{\sqrt 2}2) \approx 9.89, \text{ and}\\ y= \left(\frac{7 \pi}{2}+3 \right)(-\frac{\sqrt 2}2) \approx -9.89\text{.} \end{equation*}

We note that

\begin{equation*} \frac{dy}{dx}=\frac{2\sin(\theta)+ (2 \theta +3)(\cos(\theta))}{2\cos(\theta)+ (2 \theta +3)(-\sin(\theta))}\text{,} \end{equation*}

as in part (a). Thus, plugging in \(\theta=\frac{7\pi}4\) gives

\begin{equation*} \frac{dy}{dx}\approx0.7499\text{.} \end{equation*}
Note that the third quadrant is from \(\theta= \pi\) to \(\theta= \frac{3\pi}2\text{.}\) Using our computations from part (a), we know that

\begin{equation*} \frac{dx}{d\theta} = 2\cos(\theta)+ (2 \theta +3)(-\sin(\theta))\\ \frac{dy}{d\theta} = 2\sin(\theta)+ (2 \theta +3)(\cos(\theta))\text{.} \end{equation*}

Now, plugging into the arc length formula for a parametric equation, we get that

\begin{equation*} \text{Arc Length} = \int_\pi^{\frac{3\pi}{2}} \sqrt{ \left( \frac{dx}{d\theta}\right)^2+\left( \frac{dx}{d\theta}\right)^2} d \theta \\ = \int_\pi^{\frac{3\pi}{2}} \sqrt{ \left( 2\cos(\theta)+ (2 \theta +3)(-\sin(\theta))\right)^2+\left( 2\sin(\theta)+ (2 \theta +3)(\cos(\theta))\right)^2} d \theta \\ \approx 17.33\text{.} \end{equation*}

Subsection 6.3.5 Summary

To find the area of a region bounded by a polar curve, we think of the region as being sliced up into thin circle sectors. The exact area of the region bounded by \(r=f(\theta)\) between \(\theta=\alpha\) and \(\theta=\beta\) is

\begin{equation*} \text{Area}= \frac 12 \int_{\theta=\alpha}^{\theta=\beta} (f(\theta))^2 \, d \theta\text{.} \end{equation*}
To find the area of a region bounded by two polar curves, we subtract the smaller area from the larger one. If the two curves are \(r=f(\theta)\) and \(r=g(\theta)\text{,}\) where \(f(\theta)\geq g(\theta)\text{,}\) between \(\theta=\alpha\) and \(\theta=\beta\text{,}\) then the exact area is

\begin{equation*} \text{Area}= \frac 12 \int_{\theta=\alpha}^{\theta=\beta} (f(\theta))^2 \, d \theta-\frac 12 \int_{\theta=\alpha}^{\theta=\beta} (g(\theta))^2 \, d \theta = \frac 12 \int_{\theta=\alpha}^{\theta=\beta} (f(\theta))^2-(g(\theta))^2 \, d \theta\text{.} \end{equation*}
To compute slope and arc length of a curve in polar coordinates, we treat the curve as a parametric function of \(\theta\) and use the parametric slope and arc length formulae:

\begin{equation*} \frac{dy}{dx} = \frac{\big(\frac{dy}{d\theta}\big)}{\big(\frac{dx}{d\theta}\big)}\text{,} \end{equation*}

\begin{equation*} \text{Arc Length} = \int_{\theta=\alpha}^{\theta=\beta} \sqrt{\left(\frac{dx}{d \theta} \right)^2 + \left(\frac{dy}{d \theta}\right)^2 } \, d\theta\text{.} \end{equation*}

Exercises 6.3.6 Exercises

1. Converting Coordinates: Polar to Cartesian.

Convert the polar coordinates below to Cartesian coordinates. Give exact answers.

A. \((5, \pi/3) =\) ( , )

B. \((1, \pi) =\) ( , )

2. Converting Coordinates: Cartesian to Polar.

Convert the Cartesian coordinates below to polar coordinates. Give an angle \(\theta\) in the range \(0 \lt \theta \le 2\pi\text{,}\) and take \(r>0\text{.}\)

A. \((0, 7) =\) ( , )

B. \(({\sqrt{3}\over 2}, {1\over 2}) =\) ( , )

3. Converting Coordinates: Both Directions.

Convert the following

Convert the polar coordinates \((r,\theta)=(2,\pi)\) to Cartesian coordinates.
Convert the Cartesian coordinates \((x,y)=(0,-4)\) to polar coordinates.

4. Describing a Polar Region.

Give inequalities for \(r\) and \(\theta\) which describe the region below in polar coordinates.

(Click on the graph for a larger version.)

The two arcs shown are circular, and the region is between the two arcs and between the \(y\)-axis and line graphed, which is \(y = x\text{.}\)

\(\le r \le\)

\(\le \theta \le\)

(Write infinity to indicate a boundary at infinity.)

5. Describing a Polar Region as a Function of \(\theta\).

Give inequalities for \(r\) and \(\theta\) which describe the region below in polar coordinates.

(Click on the graph for a larger version.)

The arc shown is circular, and the region extends indefinitely in the \(y\)-direction.

\(\le r \le\)

\(\le \theta \le\)

(Write infinity to indicate a boundary at infinity, and use t for \(\theta\) if necessary.)

6. Area Inside a Cardioid.

Find the area inside the cardioid \(r=3 + 3\cos\theta\) for \(0\le\theta\le2\pi.\)

Area =

7. Area in a Region Defined by Two Curves.

Find the area lying outside \(r=6\cos\theta\) and inside \(r=3 + 3 \cos\theta\text{.}\)

Area =

8. Slope on a Polar Curve 1.

Consider the polar curve given by \(r=6\theta^2\text{.}\) Find the slope of the curve at \(\theta=\frac{\pi}{4}, \pi, 2\pi\) and \(\frac{7\pi}{3}\text{.}\)

9. Slope on a Polar Curve 2.

Consider the rose given by \(r=\sin(3\theta)\) for \(0\leq \theta \leq \pi\text{.}\) Find all the points on this curve where \(y=\frac 1 2\) and find the slopes at all of those points. (Hint: To find the points, use the trigonometric identity \(\sin(3\theta)=3\sin(\theta)-4\sin(\theta)^3)\text{,}\) rewrite the equation to be equal to 0, and then consider it as a polynomial of \(\sin^2(\theta)\text{,}\) and use that to solve for 4 values of \(\theta\text{.}\) Or, graph the rose and the line \(y=\frac 1 2\) on a graphing calculator and find the intersection points.)

10. Arc Length of a Polar Curve 1.

Consider the polar curve given by \(r=6\theta^2\text{.}\) Find the length of the curve on the intervals \(\frac \pi 2 \leq \theta \leq \frac{3\pi}{2}\text{,}\) \(0 \leq \theta \leq 2\pi\text{,}\) and \(2\pi \leq \theta \leq 4\pi\text{.}\)

11. Arc Length of a Polar Curve 2.

Consider the rose given by \(r=11\cos(5\theta)\text{,}\) which traces out a 5-petal rose over the interval \(0 \leq \theta \leq \pi\text{.}\) Find the length of the curve along its entire path, and then find the length of the curve along a single petal.

Prev Top Next