Inverse Functions
Suppose the inverse of \(f\) is a function, denoted by \(f^{-1}\text{.}\) Then
\begin{equation*}
f^{-1}(y) = x \text{ if and only if }f(x) = y.
\end{equation*}
Subsection1.10Inverse Functions
It is also useful to consider inverse functions.
Example1.22
Suppose \(g\) is the inverse function for \(f\text{,}\) and we know the following function values for \(f\text{:}\)
\begin{equation*}
f (-3) = 5, ~~ f (2) = 1, ~~ f (5) = 0.
\end{equation*}
Find \(g(5)\) and \(g(0)\text{.}\)
Solution
We know that \(g(5) = -3\) because \(f (-3) = 5\text{,}\) and \(g(0) = 5\) because \(f (5) = 0\text{.}\) Tables may be helpful in visualizing the two functions, as shown below.
| \(y=f(x)\) | |
| \(x\) | \(y\) |
| \(-3\) | \(5\) |
| \(2\) | \(1\) |
| \(5\) | \(0\) |
Interchange the columns
| \(x=g(y)\) | |
| \(y\) | \(x\) |
| \(5\) | \(-3\) |
| \(1\) | \(2\) |
| \(0\) | \(5\) |
For the function \(f\text{,}\) the input variable is \(x\) and the output variable is \(y\text{.}\) For the inverse function \(g\text{,}\) the roles of the variables are interchanged: \(y\) is now the input and \(x\) is the output.
Functions and Inverse Functions
Suppose \(f^{-1}\) is the inverse function for \(f\text{.}\) Then
\begin{equation*}
f^{-1}\left(f(x)\right) = x\text{ and }f\left(f^{-1}( y)\right) = y
\end{equation*}
as long as \(x\) is in the domain of \(f\text{,}\) and \(y\) is in the domain of \(f^{-1}\text{.}\)
We also have a method of quickly determining if a function is invertible once we have a graph of the function.
Horizontal Line Test
If no horizontal line intersects the graph of a function more than once, then its inverse is also a function.
Example1.25
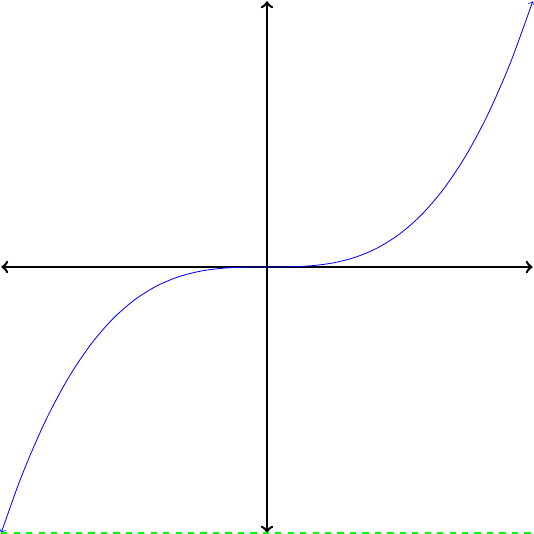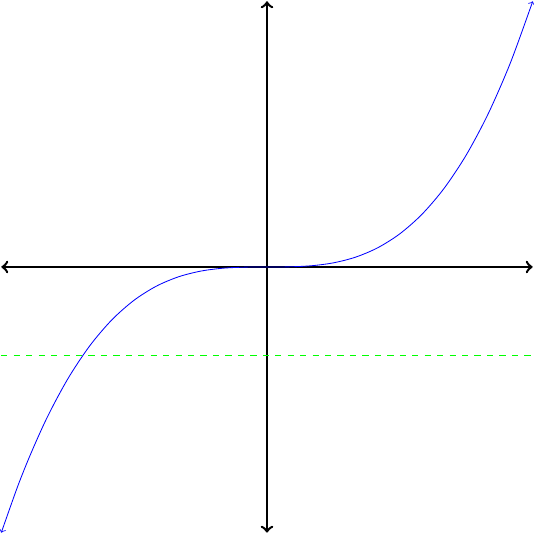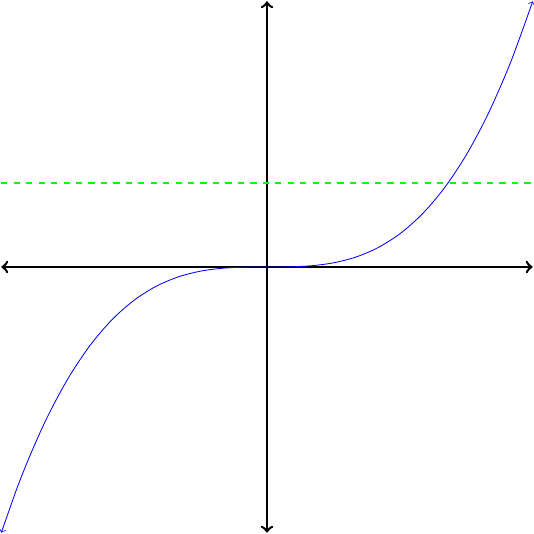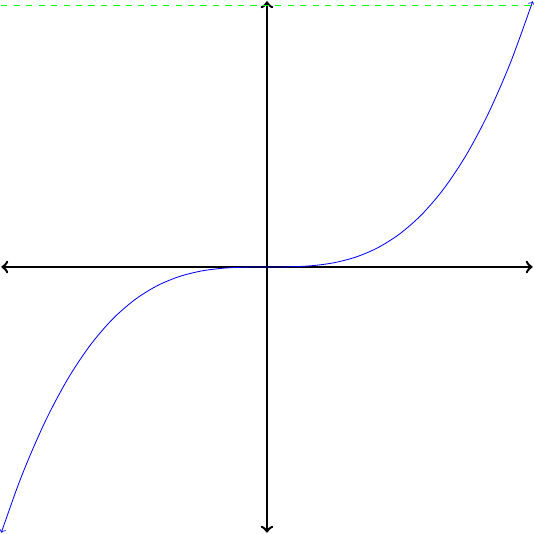
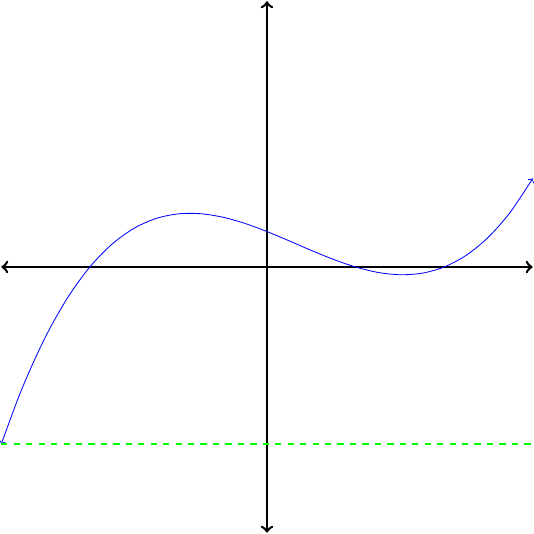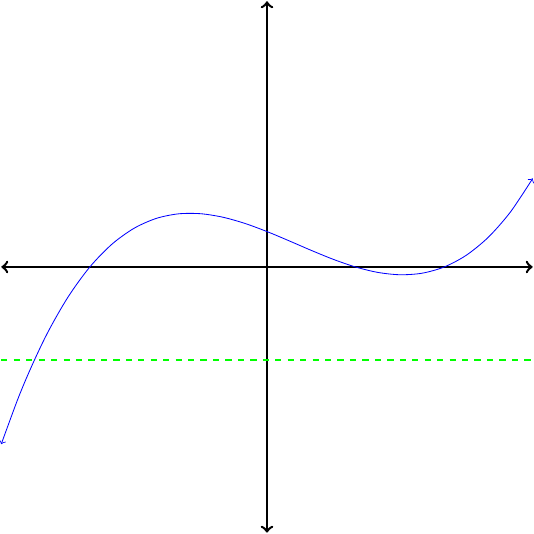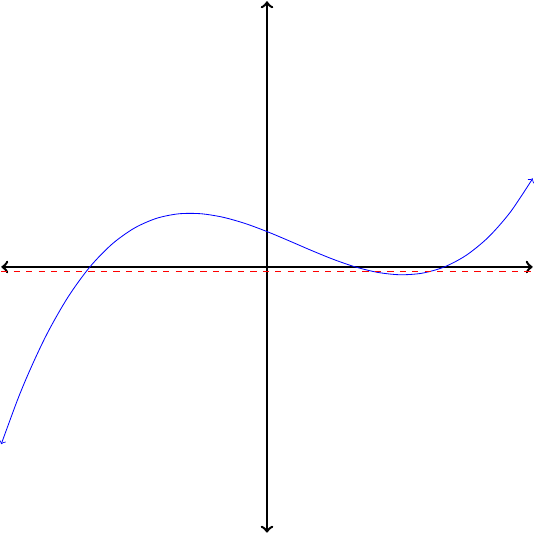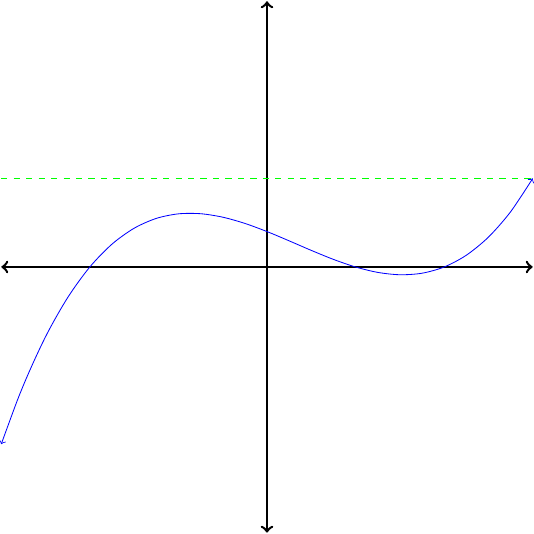
Which of the functions in Figure1.26 are invertible?
Solution
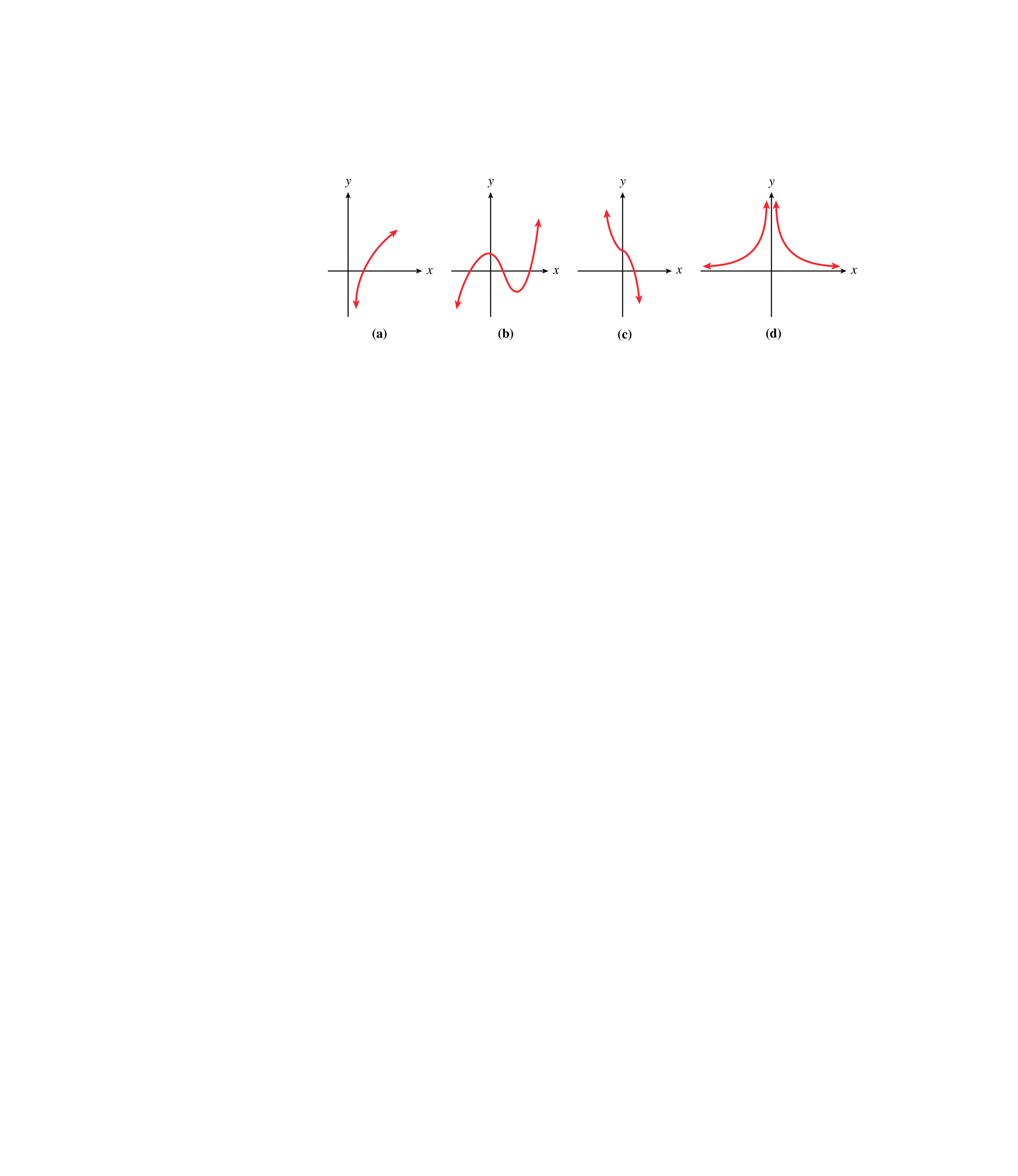
In each case, apply the horizontal line test to determine whether the function is invertible. Because no horizontal line intersects their graphs more than once, the functions pictured in Figures1.26(a) and (c) are invertible. The functions in Figures1.26(b) and (d) are not invertibe.
We have been talking about how to tell if the inverse of a function is also a function, but in practice this is not the language typicaly used. Usually we ask this same question in the form "Is the function invertible?" The following definition explains this relationship: If \(y=f(x) \) is a function such that its inverse, \(x=f^{-1}(y)\text{,}\) is also a function then we say that \(f(x) \) is an invertible function.Invertible Function
The inverse function \(f^{-1}\) undoes the effect of the function \(f\text{.}\) The function \(f(t) = 6 + 2t\) multiplies the input by \(2\) and then adds \(6\) to the result. The inverse function \(f^{-1}(H) = \dfrac{H -6}{2}\) undoes those operations in reverse order: It subtracts \(6\) from the input and then divides the result by \(2\text{.}\)
If we apply the function \(f\) to a given input value and then apply the function \(f^{-1}\) to the output from \(f\text{,}\) the end result will be the original input value. For example, if we choose \(t = 5\) as an input value, we find that \begin{align*} f(5)\amp= 6 + 2(5) = 16\amp\amp\text{ Multiply by 2, then add 6.}\\ \text{and } f^{-1}(16) \amp = \frac{16 - 6}{2} = 5.\amp\amp\text{Subtract 6, then divide by 2.} \end{align*}
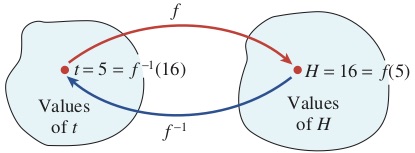
We return to the original input value, \(5\text{.}\)