Linear Equation
A linear function is a function which has a constant rate of change.
Linear relationships are relationships in which the rate of change is constant. A linear function is a function which has a constant rate of change.Linear Equation
The initial value, or the value of \(f(0)\text{,}\) is the vertical intercept of the graph, and the rate of change is the slope of the graph. Thus, we can write an equation of a line as
where the constant term, \((0,b)\text{,}\) is the vertical intercept of the line, and \(m\text{,}\) the coefficient of \(x\text{,}\) is the slope of the line. This form for an equation of a line is called the slope-intercept form.
If we write an equation of a linear function in the form,
then \(m\) is the slope of the line, and \((0,b)\) is the vertical intercept although sometimes we will accept \(b\) since the first coordinate is always \(0\text{.}\)
An icicle grows according to the formula \(H(t)=0.05t+0.12\text{,}\) where \(t\) is the time in minutes since the first measurement was take, and \(H(t)\) is the height of the icicle in centimeters.
The slope is 0.05, which tells us that the icicle's height grows by 0.05 cm each minute.
The \(y\)-intercept is \((0,0.12)\text{,}\) which tells us that the height of the icicle was 0.12 cm at the first measurement when \(t=0\text{.}\)
Samantha owns a catering business. For any party with up to 100 guests, she charges \(\$ 2,000\text{.}\) She charges \(\$ 8\) per person for each additional guest over 100. Give a formula for the cost of having Samantha cater your party as a function of the number of guests over 200.
A possible formula for the cost of having Samantha cater your party is \(C(g)=2000+8g\text{,}\) where \(g\) is the number of guests over 100.
The following formula provides a method for finding the value of the slope \(m\) when given two points on the line.
The slope of the line passing through the points \(P_1 (x_1, y_1)\) and \(P_2 (x_2, y_2)\) is given by
Compute the slope of the line between the points \((6, -3)\) and \((4, 3)\text{.}\)
Substitute the coordinates of \(Q_1\) and \(Q_2\) into the slope formula to find
This value for the slope, \(-3\text{,}\) is the same value found above.
Sometimes you will be given the slope of a line and another point on that line. The following formula is helpful in that situation.
An equation of the line that passes through the point \((x_1, y_1)\) and has slope \(m\) is
Find a formula for the line that has slope -2 and passes through the point \((-1,4)\text{.}\)
Using point-slope form, we have the line \(y=4+(-2)(x-(-1))\text{.}\)
We can also write this in slope-intercept form by simplifying: \(y=2-2x\text{.}\)
Is is also useful to introduce the term \(x\)-intercept. An \(x\)-intercept for a function \(f(x)\) is the point \((c,0)\) based on the value of \(x=c\) such that \(f(c)=0\text{.}\) We may accept the \(x\)-value \(c\) since the other coordinate is always \(0\text{.}\)\(x\)-intercept
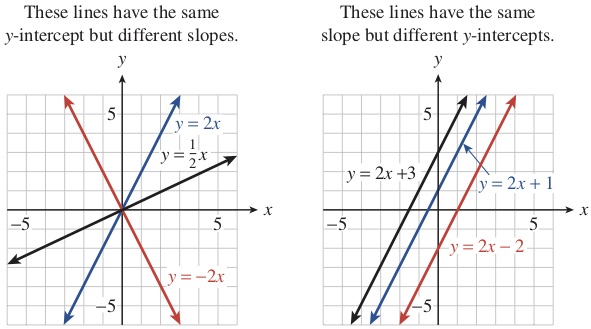
In the equation \(f (x) = mx + b\text{,}\) we call \(m\) and \(b\) parameters. Their values are fixed for any particular linear equation; for example, in the equation \(y = 2x + 3\text{,}\) \(m = 2\) and \(b = 3\text{,}\) and the variables are \(x\) and \(y\text{.}\) By changing the values of \(m\) and \(b\text{,}\) we can write the equation for any line except a vertical line (see Figure1.19). The collection of all linear functions \(f (x) = mx + b\) is called a two-parameter family of functions.