Motivating Questions
What is the mathematical notion of limit and what role do limits play in the study of functions?
How do we understand limits at asymptotes?
How do we go about determining the value of limits to infinity?
Section1.3Limits to Infinity
We have considered graphical and algebraic approaches to limits of functions. Now we will consider limits of functions with horizontal or vertical asymptotes.
SubsectionVertical and Horizontal Asymptotes
What if a function has a vertical asymptote? Consider the function graphed below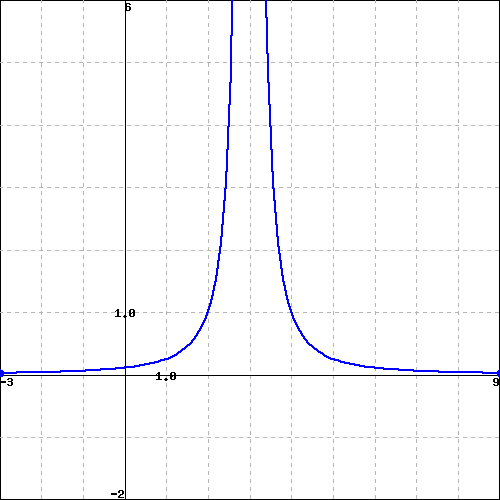 
Let us consider \(\displaystyle \lim_{x\to 3}f(x)\text{.}\) To do so we will consider the limit from either side and see if they are equal.
\begin{equation*}
\lim_{x \to 3^-} f(x) =\infty, \ \lim_{x \to 3^+} f(x) =\infty\text{.}
\end{equation*}
Since the two sides are equal then
\begin{equation*}
\lim_{x \to 3} f(x)=\infty\text{.}
\end{equation*}
Not every vertical asymptote has a limit. Consider the graph of \(\displaystyle g(x)=\frac{1}{x}\) given below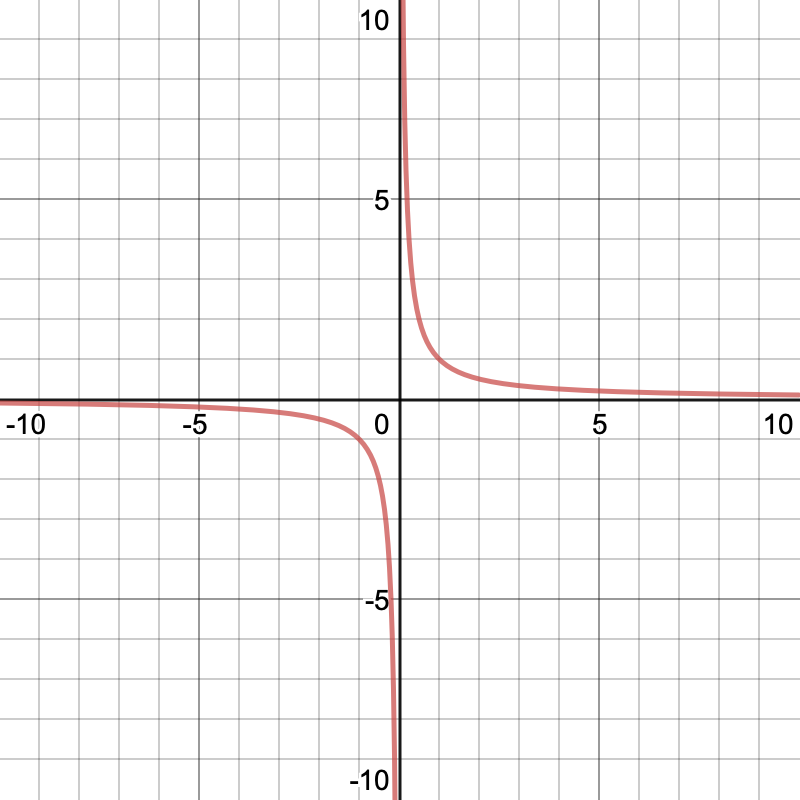 
\begin{equation*}
\lim_{x \to 0^-} g(x) =-\infty, \ \lim_{x \to 0^+} g(x) =\infty\text{.}
\end{equation*}
Since the two sides are not equal then
\begin{equation*}
\lim_{x \to 0} g(x)=DNE\text{.}
\end{equation*}
What if we are not given the graph of \(f(x)\text{?}\) A function has a vertical asymptote at a point \(x=a\) if when you try to plug in \(x=a\) you get \(\displaystyle \frac{c}{0}\text{,}\) for any non zero constant \(c\text{.}\)
Example1.16
Consider the function \(\displaystyle f(x)=\frac{x^2}{x-2}\text{.}\) The point \(x=2\) is not in the domain of \(f(x)\text{,}\) if you try to plug in \(x=2\) you get \(\displaystyle \frac{4}{0}\) which tells you that there is a vertical asymptote at \(x=2\text{.}\)
To evaluate the \(\displaystyle \lim_{x\to2} \frac{x^2}{x-2}\) must again look at the limit from the left and the limit from the right. To do so we will plug in a value of \(x\) slightly less than \(2\) and slightly greater than \(2\text{.}\)
When \(x=1.9\text{,}\) \(\displaystyle f(1.9)=\frac{1.9^2}{1.9-2}=-36.1\lt0\text{,}\) since this is negative this tells us that
\begin{equation*}
\lim_{x \to 2^-} f(x)=-\infty\text{.}
\end{equation*}
When \(x=2.1\text{,}\) \(\displaystyle f(2.1)=\frac{2.1^2}{2.1-2}=44.1\gt0\text{,}\) since this is positive this tells us that
\begin{equation*}
\lim_{x \to 2^+} f(x)=\infty\text{.}
\end{equation*}
Since the two sides are not equal then
\begin{equation*}
\lim_{x \to 2} f(x)=DNE\text{.}
\end{equation*}
Example1.17
Consider the function \(\displaystyle g(x)=\frac{x}{(x+3)^2}\text{.}\) The point \(x=-3\) is not in the domain of \(g(x)\text{,}\) if you try to plug in \(x=-3\) you get \(\displaystyle \frac{-3}{0}\) which tells you that there is a vertical asymptote at \(x=-3\text{.}\)
To evaluate the \(\displaystyle \lim_{x\to-3} \frac{x}{(x+3)^2}\text{,}\) we must again look at the limit from the left and the limit from the right. To do so we will plug in a value of \(x\) slightly less than \(-3\) and slightly greater than \(-3\text{.}\)
When \(x=-3.1\text{,}\) \(\displaystyle g(-3.1)=\frac{-3.1}{(-3.1+3)^2}=-301\lt0\text{,}\) since this is negative this tells us that
\begin{equation*}
\lim_{x \to -3^-} g(x)=-\infty\text{.}
\end{equation*}
When \(x=-2.9\text{,}\) \(\displaystyle g(-2.9)=\frac{-2.9}{(-2.9+3)^2}=-291\lt0\text{,}\) since this is negative this tells us that
\begin{equation*}
\lim_{x \to -3^+} g(x)=-\infty\text{.}
\end{equation*}
Since the two sides are equal then
\begin{equation*}
\lim_{x \to -3} g(x)=-\infty\text{.}
\end{equation*}
Finally we will look at limits to infinity:
\begin{equation*}
\lim_{x \to \infty} f(x), \ \lim_{x \to -\infty} f(x)\text{.}
\end{equation*}
First we will consider looking at the limit to infinity from the graph of a function.
Example1.18
Consider the function \(f(x)\) graphed below.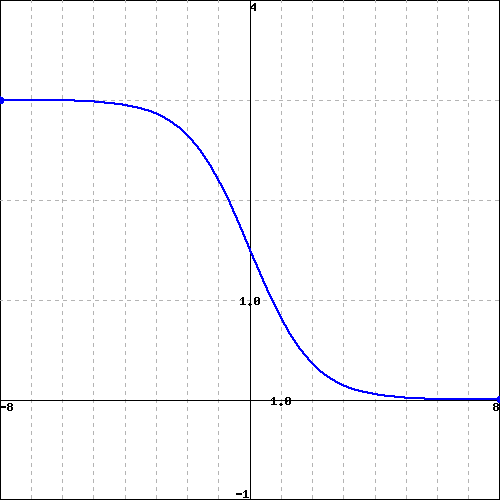 
\begin{equation*}
\lim_{x \to \infty} f(x) = 0, \ \lim_{x \to -\infty} f(x) = 3\text{.}
\end{equation*}
Understanding the limit to infinity given only the function \(f(x)\) is far more complicated. We will only consider a few special cases.
Example1.20
Consider the function \(\displaystyle f(x)=\frac{1}{x}\text{.}\) To evaluate \(\displaystyle \lim_{x\to\infty}\,\frac{1}{x}\) we will go back to the table approach
| \(x\) | \(\displaystyle f(x)=\frac{1}{x}\) |
| \(10\) | \(0.1\) |
| \(100\) | \(0.01\) |
| \(1000\) | \(0.001\) |
| \(10000\) | \(0.0001\) |
| \(100000\) | \(0.00001\) |
Observe that as \(x\) gets larger the value \(f(x)\) is approaching 0, thus
\begin{equation*}
\lim_{x \to \infty} \frac{1}{x} = 0\text{.}
\end{equation*}
Limit to Infinity
A function \(\displaystyle f(x)=\frac{1}{x^n}\) for any value of \(n\gt 0\) has the following limits to infinity and negative infinity:
\begin{equation*}
\lim_{x \to \infty} \frac{1}{x^n} = 0, \ \lim_{x \to -\infty} \frac{1}{x^n}=0\text{.}
\end{equation*}
We can use this to evaluate limits of rational functions that have a polynomial in both the numerator and denominator. Let \(r(x) \) be a rational function and let \(n>0 \) be the highest power of \(x\) that appears in \(r(x) \text{.}\) Then \(\displaystyle \lim_{x \to \infty} r(x) = \lim_{x \to \infty} \left( r(x)\cdot \frac{\left( \frac{1}{x^n} \right)}{\left(\frac{1}{x^n}\right)}\right)\) because \(\displaystyle \lim_{x \to \infty} \frac{\left(\frac{1}{x^n}\right)}{\left(\frac{1}{x^n}\right)} = 1 \) so we can use the product property of limits without changing the value of \(\lim_{x \to \infty}r(x) \text{.}\)
Example1.22
Consider the function \(\displaystyle f(x)=\frac{2x^2+3x+3}{3x^2+4x-4}\text{.}\) To evaluate \(\displaystyle \lim_{x\to \infty}f(x)\) first identify the highest power of \(x\) in either the numerator or denominator, here \(x^2\text{.}\) Distribute \(\frac{1}{x^2}\) to every term in the numerator and denominator.
\begin{equation*}
\lim_{x \to \infty} \frac{2x^2+3x+3}{3x^2+4x-4}=\lim_{x \to \infty} \frac{\left(2x^2+3x+3\right)}{\left(3x^2+4x-4\right)}\cdot \frac{\frac{1}{x^2}}{\frac{1}{x^2}}=\lim_{x \to \infty} \frac{\left(2x^2+3x+3\right)\frac{1}{x^2}}{\left(3x^2+4x-4\right)\frac{1}{x^2}}=
\end{equation*}
\begin{equation*}
=\lim_{x \to \infty} \frac{\frac{2x^2}{x^2}+\frac{3x}{x^2}+\frac{3}{x^2}}{\frac{3x^2}{x^2}+\frac{4x}{x^2}-\frac{4}{x^2}}=\lim_{x \to \infty} \frac{2+\frac{3}{x}+\frac{3}{x^2}}{3+\frac{4}{x}-\frac{4}{x^2}}=\frac{2}{3}\text{.}
\end{equation*}
After we cancel the \(x\) any term that has an \(x\) in the denominator goes to \(0\text{.}\)
Example1.23
Consider the function \(\displaystyle g(x)=\frac{4x^2+5x+2}{6x^3+4x^2+5}\text{.}\) To evaluate \(\displaystyle \lim_{x\to \infty}f(x)\) first identify the highest power of \(x\) in either the numerator or denominator, here \(x^3\text{.}\) Divide every term by the highest power of \(x\text{,}\) note that this will not change the limit because of the properties of limits. We are just skipping some of the algebraic steps in the previous example.
\begin{equation*}
\lim_{x \to \infty} \frac{4x^2+5x+2}{6x^3+4x^2+5}=\lim_{x \to \infty} \frac{\frac{4x^2}{x^3}+\frac{5x}{x^3}+\frac{2}{x^3}}{\frac{6x^3}{x^3}+\frac{4x^2}{x^3}+\frac{5}{x^3}}=\lim_{x \to \infty} \frac{\frac{4}{x}+\frac{5}{x^2}+\frac{2}{x^3}}{6+\frac{4}{x^2}+\frac{5}{x^3}}=\frac{0}{6}=0\text{.}
\end{equation*}
SubsectionSummary
- To compute limits at vertical asymptotes, we must compute both the left and right side limits and determine if they are equal or not.
- A function has a limit at infinity (or negative infinity) if it approaches a horizontal asymptote. In particular, the graph of \(f(x) = \frac{1}{x^n} \) (with \(n > 0\)) has a horizontal asymptote at \(y = 0\text{,}\) so \(\displaystyle \lim_{x \to \infty} f(x) = 0 = \lim_{x \to -\infty} f(x) \text{.}\)
- To compute the limits at infinity of a rational function, one can divide every term by the highest power of \(x\) appearing in the numerator or denominator and applying the observation for limits at infinity of \(\frac{1}{x^n} \text{.}\)