Skip to main content
\(\newcommand{\dollar}{\$} \DeclareMathOperator{\erf}{erf} \DeclareMathOperator{\arctanh}{arctanh} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Section5.5Consumer and Producer Surplus

Motivating Questions

  • What is the equilibrium point, what does it represent, and how does one compute it?

  • What is the consumer surplus, and how does one compute it?

  • What is the producer surplus, and how does one compute it?

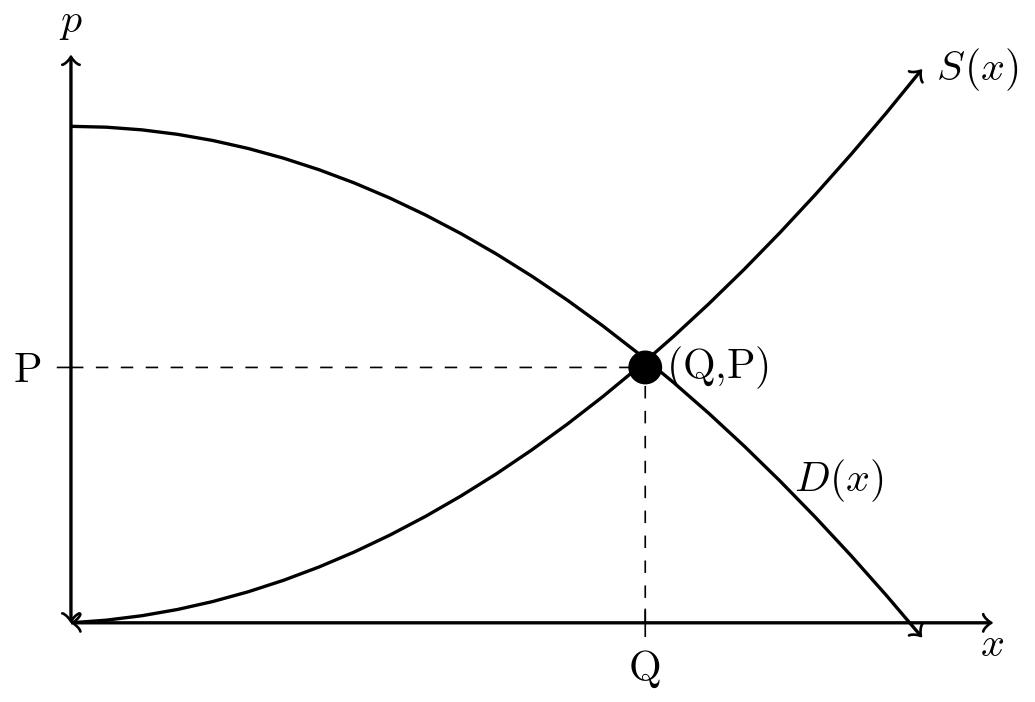
It is of interest to both consumers and producers to know the best price to buy or sell a product. Let us consider the demand curve, \(p=D(x)\text{,}\) the price per unit that a consumer is willing to pay for \(x\) units of a product, and the supply curve, \(p=S(x)\text{,}\) the price per unit that the producer is willing to accept for the sale of \(x\) units.

As the number of units \(x\) that are produced and sold increases, the demand curve, \(D(x)\) decreases. This is because consumers expect to pay less per unit for large quantities of the product. At a small scale, you can see this anytime you visit the grocery store: the price per unit when you buy a single item is almost always much more than the price per item when you buy in bulk. Graphically, \(D(x)\) is represented as a decreasing function.

As the number of units \(x\) that are produced and sold increases, the supply curve, \(S(x)\) increases. This is because a higher price per unit sold is an incentive for the producer to make more units available for sale. Graphically, \(S(x)\) is represented by an increasing function. The equilibrium point (Q,P) is the point at which the supply meets demand, or the point of intersection of the curves \(S(x)=D(x)\text{.}\)

Figure5.75Equilibrium Point at the intersection of the Supply and Demand Curves

SubsectionConsumer and Producer Surplus

Some consumers are willing to spend more on a product than the equilibrium price. The total difference between the equilibrium price of an item and the higher price a consumer is willing to spend is call the Consumer Surplus at the equilibrium and is the area between the curves \(D(x)\) and the horizontal line \(y=P\text{,}\) the equilibrium price (see Figure5.76).

Similarly, some producers are willing to sell a product at a price lower than the equilibrium price. The total difference between the equilibrium price of the item and lower price producers are willing to accept is called the Producer Surplus at the equilibrium. This is also an area between two curves: the horizontal line \(y=P\) and the supply curve, \(S(x)\text{,}\) (see Figure5.76).

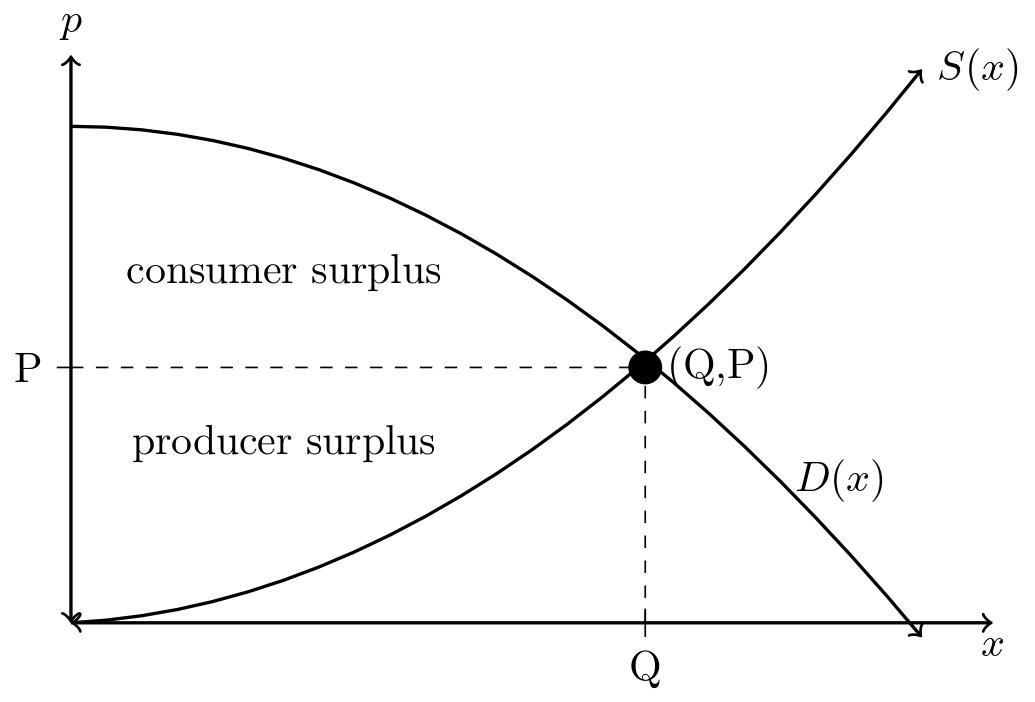
Figure5.76Graphs of the Supply and Demand Curves

In Section 4.4 we saw that the area between two curves, \(f(x)\) and \(g(x)\text{,}\) can be determined by the integral \(\displaystyle \int_a^b \left(f(x)-g(x)\right)dx\text{,}\) where \(g(x)\) has y-values below \(f(x)\) on the interval \([a,b]\text{.}\) Since the producer and consumer surpluses are represented by areas between two curves, then we can use integration to calculate these values.

Consumer Producer Surplus

Let \(p=D(x)\) describe the demand function for a product and \(p=S(x)\) be the supply function for the same product. The equilibrium point \((Q,P)\) is the point where \(D(x)=S(x)\text{.}\)

The Consumer Surplus at the equilibrium point is:

\begin{equation*} \int\limits_0^Q \left(D(x)-P\right) dx=\int\limits_0^Q D(x) dx-QP \end{equation*}

The Producer Surplus at the equilibrium point is:

\begin{equation*} \int\limits_0^Q \left(P-S(x)\right) dx=QP-\int\limits_0^Q S(x) dx \end{equation*}

Example5.77

Suppose the supply function for selling \(x\) units is given by the equation \(\displaystyle S(x)=250+5x\text{;}\) the demand function for \(x\) units is given by \(\displaystyle D(x)=1000-10x\text{.}\) Find the producer and consumer surplus and explain what they represent.

Solution: The first step is to find the equilibrium quantity, \(Q\text{.}\) To do this we set \(S(x)=D(x)\) and solve for \(x\text{:}\)

\begin{equation*} 250+5x=1000-10x \implies 15x=750 \implies x=50 \end{equation*}

That is the equilibrium quantity is \(Q=50\) units sold.

Next find the equilibrium price, \(P\) by plugging in \(x=50\) into either \(S(x)\) or \(D(x)\text{.}\)

\begin{equation*} S(50)=250+5(50)=500 \end{equation*}

And

\begin{equation*} D(50)=1000-10(50) = 500. \end{equation*}

Thus the equilibrium price is \(P=\$500\text{.}\)

The consumer surplus is

\begin{equation*} \int\limits_0^Q \left(D(x)-P\right)dx=\int\limits_0^{50} \left(1000-10x-500\right)dx=\int\limits_0^{50} \left(500-10x\right)dx \end{equation*}
\begin{equation*} =\left.\left(500x-\frac{10x^2}{2}\right)\right|_0^{50}=\left(500(50)-5(50)^2)\right)-0=\$12500 \end{equation*}

Thus the advantage to the consumer who buys at the equilibrium price is \(\$12,500\text{.}\)

The Producer Surplus is

\begin{equation*} \int\limits_0^Q \left(P-S(x)\right)dx=\int\limits_0^{50} \left(500-(250+5x)\right)dx=\int\limits_0^{50}\left(250-5x\right)dx \end{equation*}
\begin{equation*} =\left.\left(250x-\frac{5x^2}{2}\right)\right|_0^{50}=\left(250(50)-\frac{5(50)^2}{2}\right)-0=\$6250 \end{equation*}

This means that the producer will have additional income of \(\$6,250\) if they sell their product at the equilibrium price.

Example5.78

The supply function for \(x\) barrels of oil is given (in dollars) by \(S(x)=x^2+10x\text{,}\) and the demand function is given (in dollars) by \(D(x)=900-20x-x^2\text{.}\)

  1. Find the point \((Q,P)\) at which supply and demand are in equilibrium.

  2. Find the consumer surplus.

  3. Find the producer surplus.

Answer

  1. The equilibrium point is \((15,375)\text{.}\)

  2. The consumer surplus is \(\$6,450\text{.}\)

  3. The producer surplus is \(\$3,375\text{.}\)

Solution

  1. To find the point \((Q,P)\text{,}\) set the supply and demand functions equal to each other:

    \begin{equation*} x^2+10x=900-20x-x^2. \end{equation*}

    Using addition and subtraction, bring all the terms to one side:

    \begin{equation*} 2x^2+30x-900=0 \end{equation*}

    and factor

    \begin{equation*} 2(x-15)(x+30)=0. \end{equation*}

    Since the quantity of items that are sold must be positive, \(Q=15\) items. Then to find the equilibrium price plug into either \(S(x)\) or \(D(x)\text{.}\)

    \begin{equation*} S(15)=15^2+10(15)=375 \end{equation*}

    and

    \begin{equation*} D(15)=900-20(15)-15^2=375 \end{equation*}

    Thus the equilibrium is at \((15,375)\text{.}\)

  2. The consumer surplus is

    \begin{equation*} \int\limits_0^Q \left(D(x)-P\right)dx=\int\limits_0^{15} \left(900-20x-x^2-375\right)dx \end{equation*}
    \begin{equation*} =\int\limits_0^{15} \left(525-20x-x^2\right)dx=\left.\left(525x-\frac{20x^2}{2}-\frac{x^3}{3}\right)\right|_0^{15} \end{equation*}
    \begin{equation*} =\left(525(15)-20(15)^2-\frac{15^3}{3})\right)-0=\$6450. \end{equation*}

  3. The producer surplus is

    \begin{equation*} \int\limits_0^Q \left(P-S(x)\right)dx=\int\limits_0^{15} \left(375-(x^2+10x)\right)dx \end{equation*}
    \begin{equation*} =\int\limits_0^{15}\left(375-10x-x^2\right)dx=\left.\left(375x-\frac{10x^2}{2}-\frac{x^3}{3}\right)\right|_0^{15} \end{equation*}
    \begin{equation*} =\left(375(15)-5(15)^2-\frac{15^3}{3}\right)-0=\$3375. \end{equation*}
Example5.79

Suppose \(\displaystyle D(x)=\frac{196}{\sqrt{x}}\) is the price, in dollars per unit, that consumers are willing to pay for \(x\) units of an item, and \(S(x)=\sqrt{x}\) is the price, in dollars per unit, that producers are willing to accept for \(x\) units.

  1. Find the point \((Q,P)\) at which supply and demand are in equilibrium.

  2. Find the consumer surplus.

  3. Find the producer surplus.

Answer

  1. The equilibrium point is \((196,14)\text{.}\)

  2. The consumer surplus is \(\$2,744\text{.}\)

  3. The producer surplus is \(\$914.67\text{.}\)

Solution

  1. To find the point \((Q,P)\) set the supply and demand functions equal

    \begin{equation*} \frac{196}{\sqrt{x}}=\sqrt{x} \end{equation*}

    Multiply both sides by the \(\sqrt{x}\) to solve for

    \begin{equation*} 196=\sqrt{x}\sqrt{x}=x \end{equation*}

    Thus the equilibrium quantity is \(Q=196\) units sold. Then to find the equilibrium price plug into either \(S(x)\) or \(D(x)\text{.}\)

    \begin{equation*} S(196)=\sqrt{196}=14 \end{equation*}

    and

    \begin{equation*} D(196)=\frac{196}{\sqrt{196}}=14 \end{equation*}

    Thus the equilibrium is at \((196,14)\text{.}\)

  2. The consumer surplus is

    \begin{equation*} \int\limits_0^Q \left(D(x)-P\right)dx=\int\limits_0^{196} \left(\frac{196}{\sqrt{x}}-14\right)dx \end{equation*}
    \begin{equation*} =\int\limits_0^{196} \left(196x^{-1/2}-14\right)dx=\left.\left(\frac{196x^{1/2}}{1/2}-14x\right)\right|_0^{196} \end{equation*}
    \begin{equation*} =\left(392(196)^{1/2}-14(196))\right)-0=\$2744 \end{equation*}

  3. The producer surplus is

    \begin{equation*} \int\limits_0^Q \left(P-S(x)\right)dx=\int\limits_0^{196} \left(14-(\sqrt{x})\right)dx \end{equation*}
    \begin{equation*} =\int\limits_0^{196}\left(14-x^{1/2}\right)dx=\left.\left(14x-\frac{x^{3/2}}{3/2}\right)\right|_0^{196} \end{equation*}
    \begin{equation*} =\left(14(196)-\frac{2}{3}(196)^{3/2}\right)-0=\$914.66 \end{equation*}

SubsectionSummary

  • If we let \(p = D(x) \) be the demand curve and \(p = S(x) \) be the supply curve, then the equilibrium point is the point \((Q, P) \) at which the supply meets demand; in other words, where \(S(x) = D(x) \text{.}\)

  • The consumer surplus is the difference between the equilibrium price of an item and the higher price that a consumer is willing to spend. This is also the area between the curves \(D(x) \) and the horizontal line \(y=P \text{.}\) We can use integration to calculate this area, so the consumer surplus at the equilibrium point is \(\int_0^Q D(x)dx - QP \text{.}\)

  • The producer surplus is the difference between the equilibrium price of an item and the lower price at which a producer is willing to sell that item. This is also the area between the curves \(S(x) \) and the horizontal line \(y=P \text{.}\) As with the consumer surplus, we can use integration to calculate this area, so the producer surplus at the equilibrium point is \(QP - \int_0^Q S(x)dx \text{.}\)

SubsectionExercises