Motivating Questions
What is a tangent line?
How can we sketch a tangent line?
How do we find an equation for the tangent line?
Section2.5The Tangent Line
Recall that a line can be written as \(y = m(x- x_0) + y_0\text{,}\) where \(m \) is the slope of the line and \((x_0, y_0) \) is a point on the line. Using this information and our new derivative rules, we are in a position to quickly find the equation for the line which intersects a curve at a particular point and has the same slope, which we call the tangent line. Specifically, we have the following definition.
Given a differentiable function \(f\) and a point \((x_0,y_0)\) the equation for the tangent line to the function \(f\) at \((x_0,y_0)\) is given byThe Tangent Line
\begin{equation*}
y=f'(x_0)(x-x_0)+y_0.
\end{equation*}
We will look more at tangent lines in future sections but the basic ideas appear here. Specifically, if we know data about a function at a specific point such as it's value at that point and rate of change at that point then we can estimate its value at a future point.
SubsectionSketching the Tangent Line
If the tangent line at \(x = a\) exists, the graph of \(f\) looks like a straight line when viewed up close at \((a,f(a))\text{.}\) In Figure2.41 below, we zoom in on \(f(x)\) and its tangent line at \((a,f(a))\text{.}\) Note how the tangent line sits relative to the curve \(y = f(x)\) at \((a,f(a))\text{,}\) and how closely it resembles the curve near \(x = a\text{.}\)
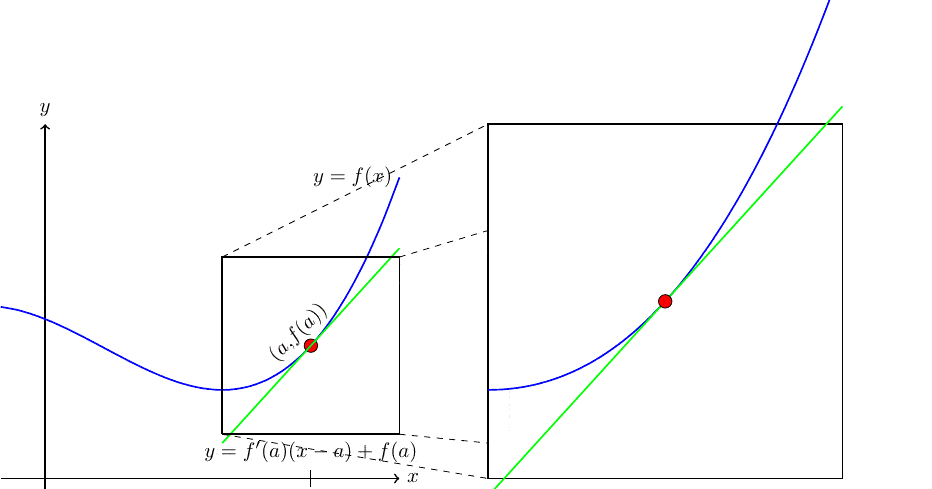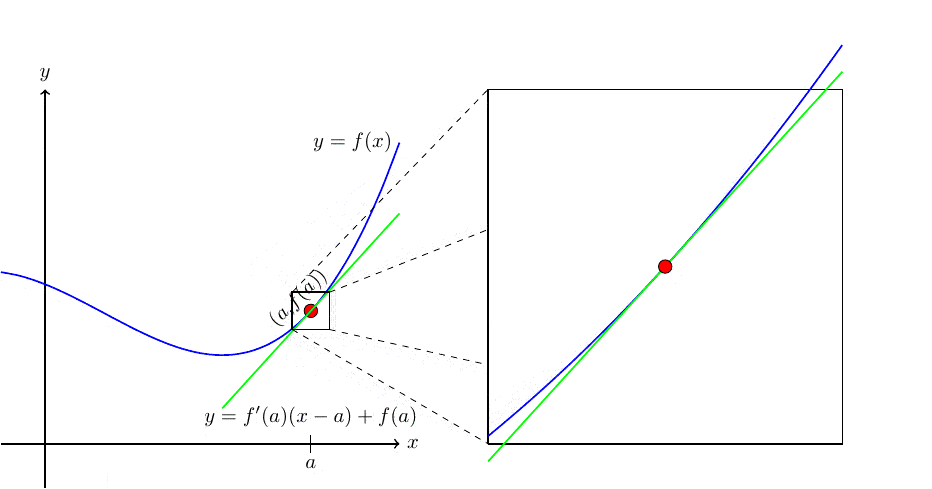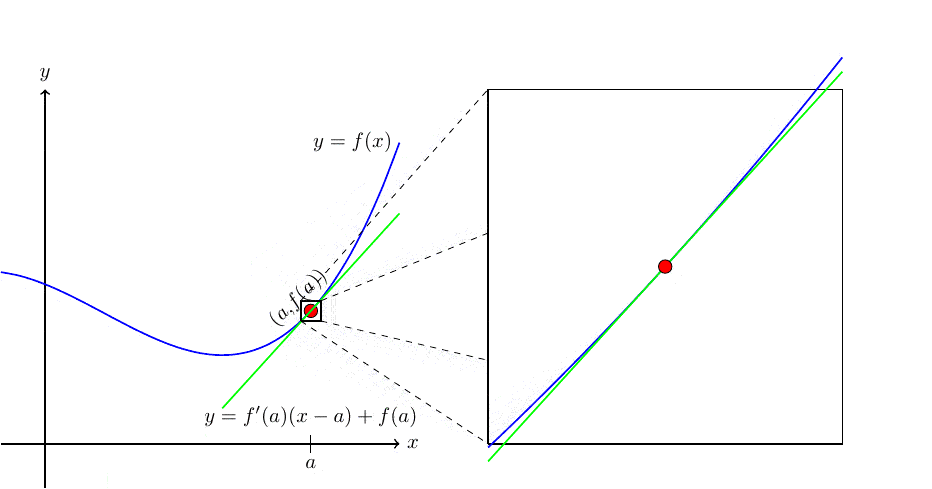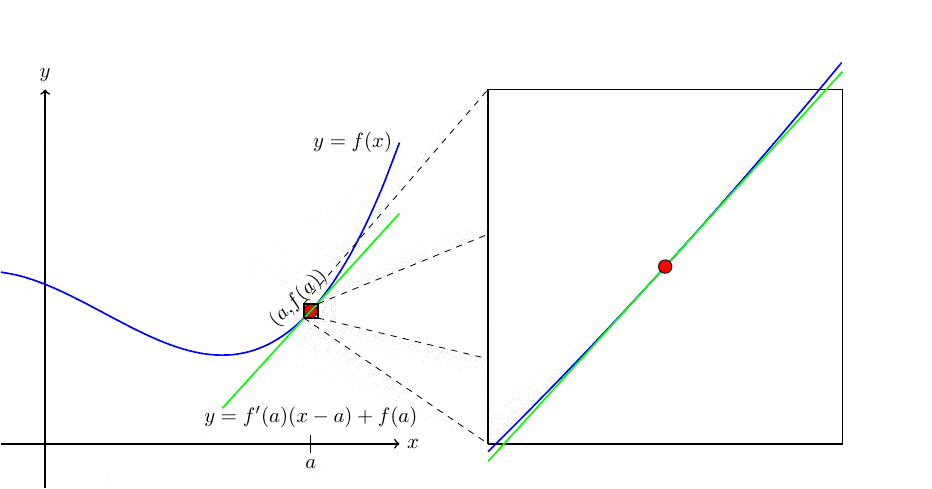
With this information, we may informally sketch a tangent line by estimating the rate of change at a point \(x = a \) and following a straight line.
Example2.42
Below in Figure2.43 is the graph of a function, \(g(x) \text{.}\) We can sketch the tangent line at several different points.
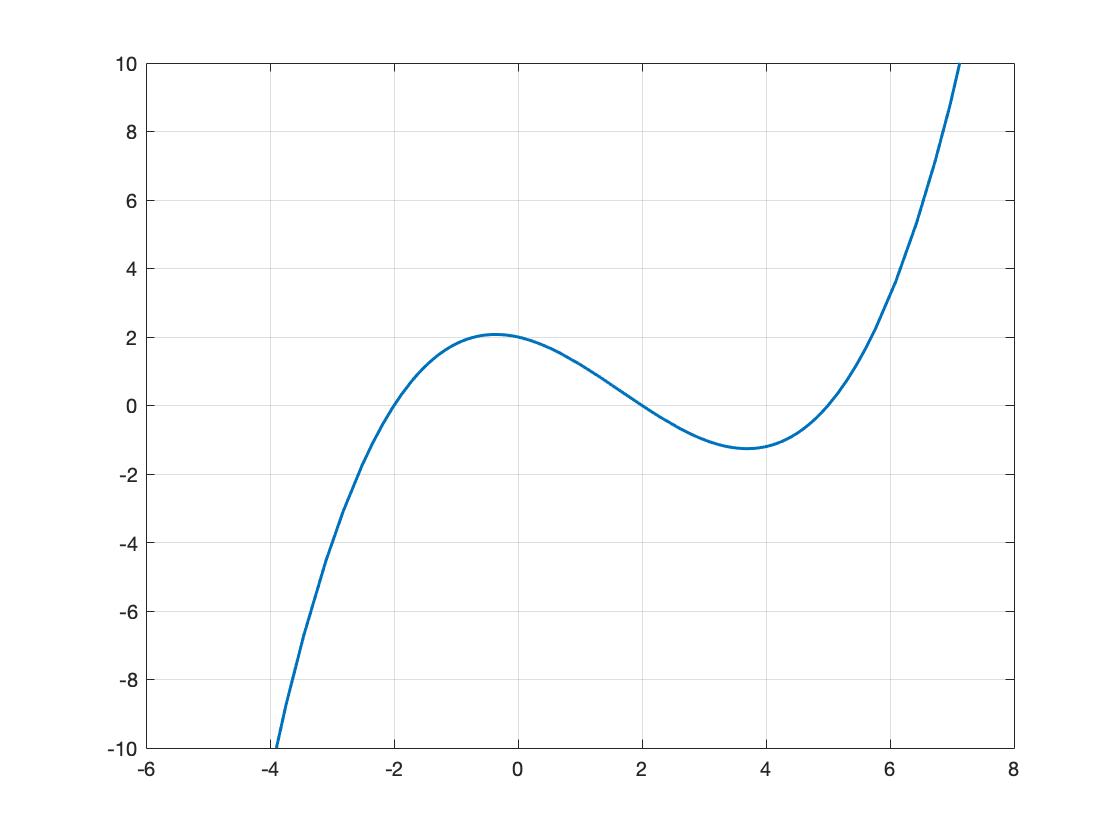
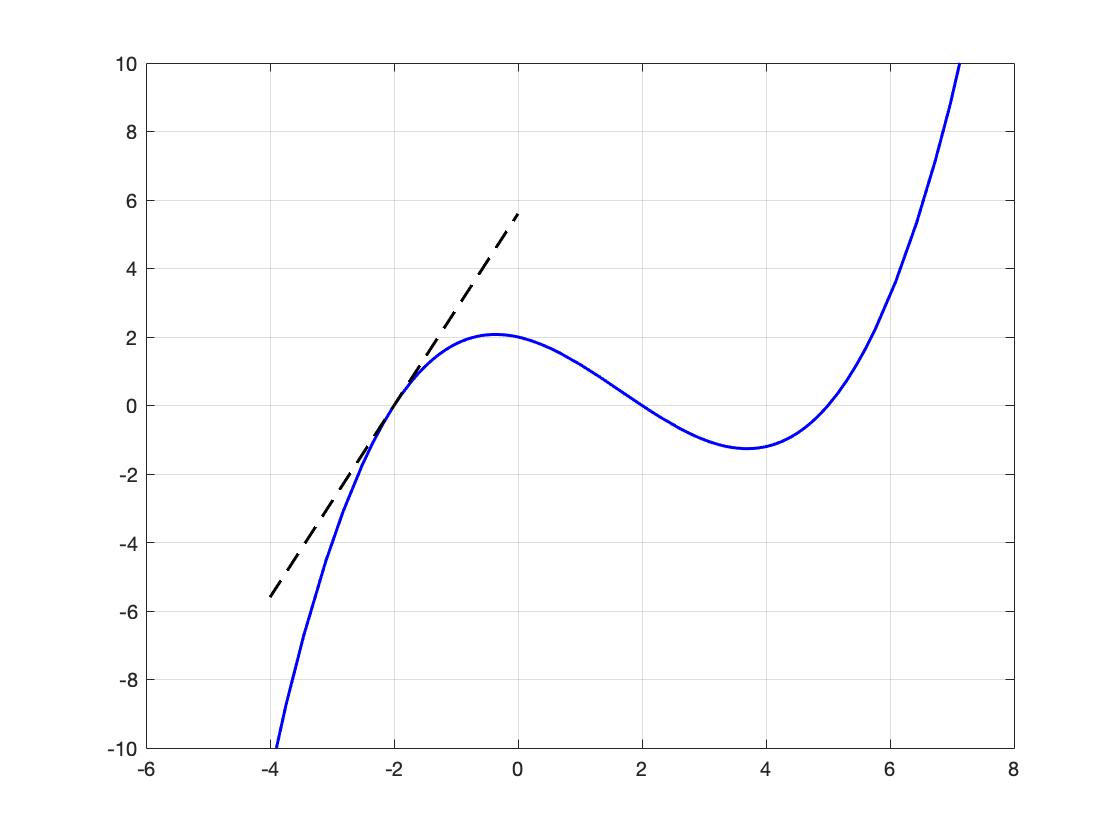
Notice that at the point \(x = -2\text{,}\) the slope of the tangent line is positive, and at the point \(x = 2 \text{,}\) the slope of the tangent line is negative.
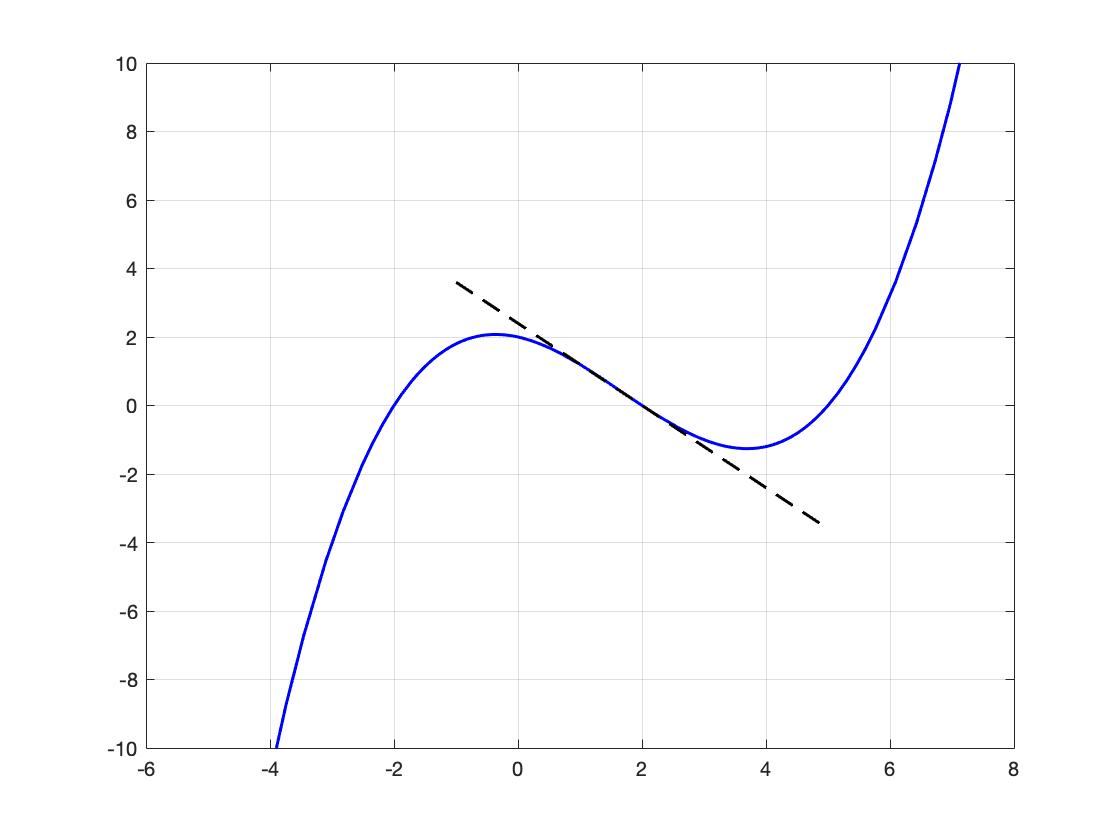
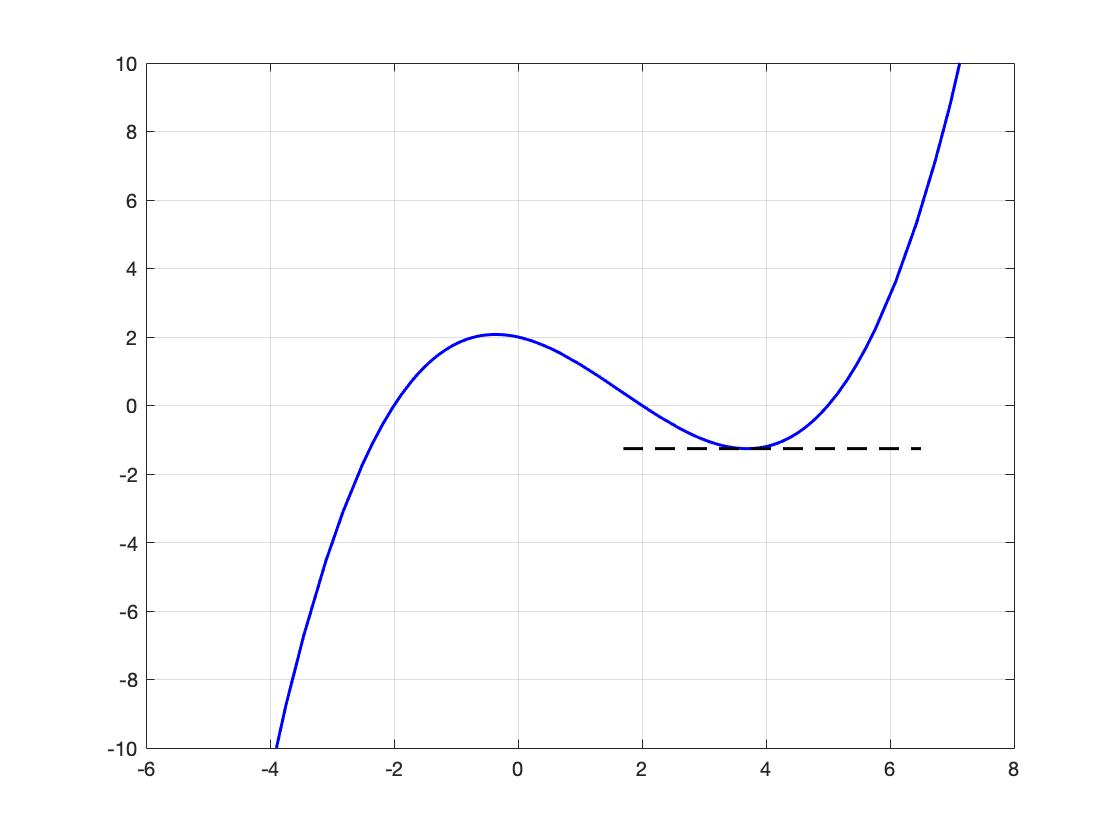
At roughly \(x = 3.7 \text{,}\) the slope of the tangent line is zero.
Example2.47
Below is the graph of a function \(f(x) \text{.}\)
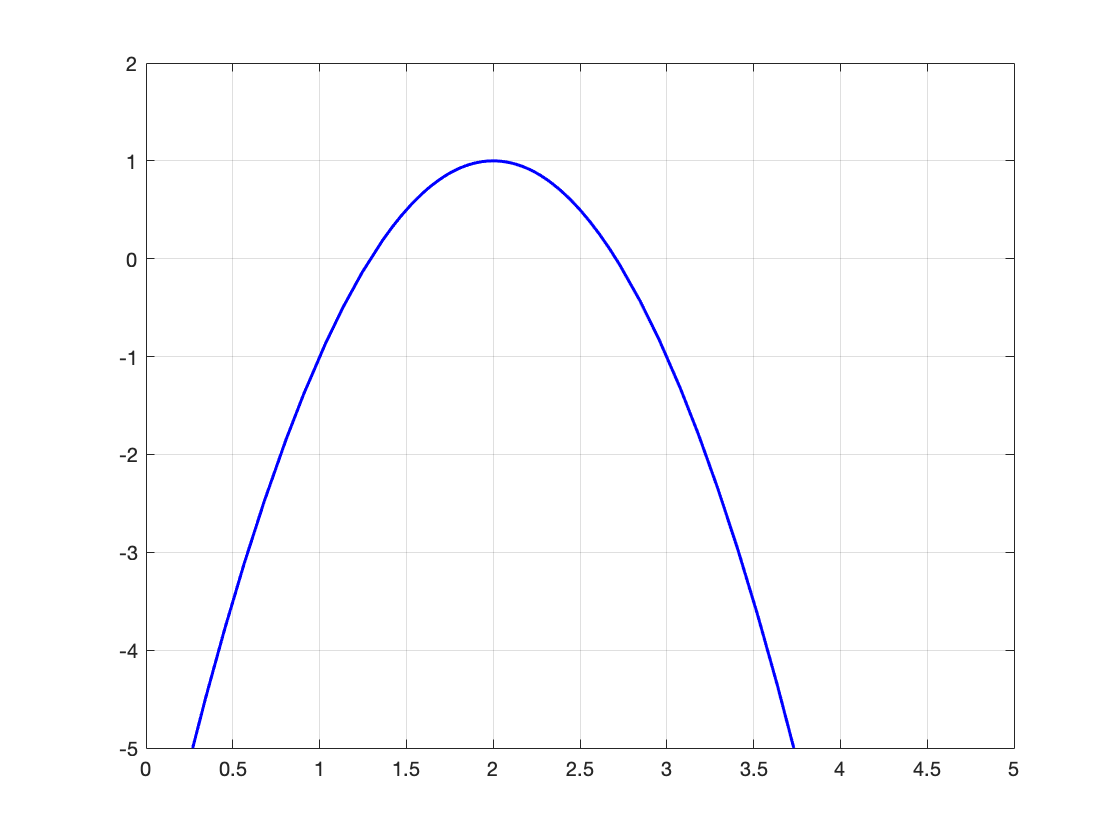
Give the \(x\)-coordinate of a point where:
The slope of the tangent line is negative.
The slope of the tangent line is positive.
The slope of the tangent line is zero.
Answer
Any \(x \)-coordinate in the domain \((2, \infty) \) is suitable
Any \(x \)-coordinate in the domain \((-\infty, 2) \) is suitable
The only \(x \) coordinate with a tangent line of slope zero is \(x = 2 \text{.}\)
SubsectionFinding the Tangent Line
When finding the tangent line for a function \(f \text{,}\) we need three pieces of information:
The value, \(x_0 \text{,}\) at which we are finding the tangent line.
The value of the function at \(x = x_0 \text{,}\) \(f(x_0) \text{.}\)
The value of the derivative at \(x = x_0 \text{,}\) \(f'(x_0) \text{.}\)
Once we have all of those pieces of information, we can plug into the given formula to find an equation for the tangent line.
Example2.49
Suppose \(f(x) = -\dfrac{4}{x} \text{.}\) To find the tangent line at \(x = -2 \text{,}\) we find the other two pieces of necessary information:
First, we find \(f(-2) \text{:}\)
\begin{align*}
f(-2)= \mathstrut \amp \frac{-4}{-2}\\
=\mathstrut \amp 2.
\end{align*}
Next, we find \(f'(-2) \text{:}\)
\begin{align*}
f'(x)= \mathstrut \amp -\left(\frac{-4}{x^2}\right)\\
= \mathstrut \amp \frac{4}{x^2},\\
f'(-2)= \mathstrut \amp \frac{4}{(-2)^2}\\
= \mathstrut \amp \frac{4}{4}\\
= \mathstrut \amp 1.
\end{align*}
Putting the pieces together, we have
\begin{equation*}
y = 1(x+2) +2
\end{equation*}
as an equation for the tangent line.
Example2.50
Find an equation for the line tangent to \(g(x)= 3\sqrt{x} - x \) at \(x = 9\text{.}\)
Compute \(g(9) \text{;}\) this will give you the \(y-\)value of the point on the tangent line.
Compute the derivative \(g'(x)\text{.}\)
Compute \(g'(9) \text{;}\) this is the slope of the tangent at \(x = 9 \text{,}\) the \(x\)-value given.
-
Put together in point slope form:
\begin{equation*} y = g'(9)(x-9) + g(9). \end{equation*}
Answer
Solution
\(g(9)= 0 \)
\(g'(x)= \frac{3}{2\sqrt{x}} -1\)
\(g'(9) = - \frac{1}{2}\)
\(y = -\frac{1}{2}(x-9)\)
- \begin{align*} g(9)= \mathstrut \amp 3\sqrt{9} - 9\\ =\mathstrut \amp 3(3) - 9 \\ =\mathstrut \amp 0. \end{align*}
-
First, we will rewrite \(g(x) \text{:}\)
\begin{equation*} g(x) = 3x^{1/2} - x. \end{equation*}Then,
\begin{align*} g'(x) =\mathstrut \amp \frac{1}{2}\left(3x^{-1/2}\right) -1 \\ = \mathstrut \amp \frac{3}{2\sqrt{x}}-1. \end{align*} -
Plugging in \(x = 9 \) into part b.,
\begin{align*} g'(9) = \mathstrut \amp \frac{3}{2\sqrt{9}} - 1 \\ =\mathstrut \amp \frac{3}{2(3)} - 1\\ =\mathstrut \amp \frac{1}{2} - 1\\ =\mathstrut \amp - \frac{1}{2}. \end{align*} -
Combining the above three parts,
\begin{align*} y = \mathstrut \amp -\frac{1}{2}(x-9) + 0 \\ =\mathstrut \amp -\frac{1}{2}(x-9). \end{align*}
Example2.51
Each of the following questions asks you to use derivatives to answer key questions about functions. Be sure to think carefully about each question and to use proper notation in your responses.
If \(\displaystyle h(z)=\sqrt{z}+\frac1z\text{,}\) find the slope of the tangent line to the graph of \(y=h(z)\) at the point where \(z = 4\text{.}\)
Find an equation for the tangent line to the curve \(y=p(a)\text{,}\) where \(p(a) = 3a^4 - 2a^3 + 7a^2 - a + 12\text{,}\) at the point where \(a=-1\text{.}\)
What is the difference between being asked to find the slope of the tangent line (asked in (a)) and the equation of the tangent line (asked in (b))?
Answer
Solution
\(\displaystyle h'(4) = \frac{3}{16}\text{.}\)
\(y - 25 = -33(a+1)\text{.}\)
The slope is a number and is only one piece of the equation, which contains more information.
Note that since \(\displaystyle h(z) = z^{\frac{1}{2}} + z^{-1}\text{,}\) we have \(\displaystyle h'(z) = \frac{1}{2}z^{-\frac{1}{2}} - z^{-2}=\frac{1}{2\sqrt{z}}-\frac{1}{z^2}\text{.}\) Thus, \(\displaystyle h'(4) = \frac{1}{2\sqrt4} - \frac{1}{4^2} = \frac{1}{4} - \frac{1}{16} = \frac{3}{16}\text{.}\) Therefore the slope of the tangent line to the graph of \(y=h(z)\) at the point where \(z = 4\) is \(\frac{3}{16}\text{.}\)
Given \(p(a) = 3a^4 - 2a^3 + 7a^2 - a + 12\text{,}\) first observe that \(p(-1) = 3 + 2 + 7 + 1 + 12 = 25\text{,}\) so the tangent line will pass through the point \((-1,25)\text{.}\) Furthermore, since \(p'(a) = 12a^3 - 6a^2 + 14a - 1\text{,}\) we know that the slope of the tangent line is \(p'(-1) = -12 - 6 - 14 - 1 = -33\text{.}\) An equation of the tangent line is therefore \(y - 25 = -33(a+1)\text{.}\) Equivalently, \(y=-33a-8\) is an equation of this tangent line.
Finding the slope of the tangent line only requires knowing the value of the derivative at a particular input. In contrast, finding the equation of the tangent line additionally requires knowing the value of the original function at that same input. In other words, the slope is just a number, whereas the equation incorporates additional information that together with the slope is sufficient to actually graph the tangent line.
SubsectionSummary
The tangent line to the graph of \(f(x) \) at \((a, f(a)) \) closely resembles the curve near \(x = a \text{.}\)
-
The equation for the tangent line of \(f(x) \) at \(x = a \) is
\begin{equation*} y = f'(a)(x-a) + f(a), \end{equation*}and so the necessary information to find is the value of the function at \(x = a \text{,}\) the derivative \(f'(x) \text{,}\) and the value of the derivative at \(x=a \text{.}\)