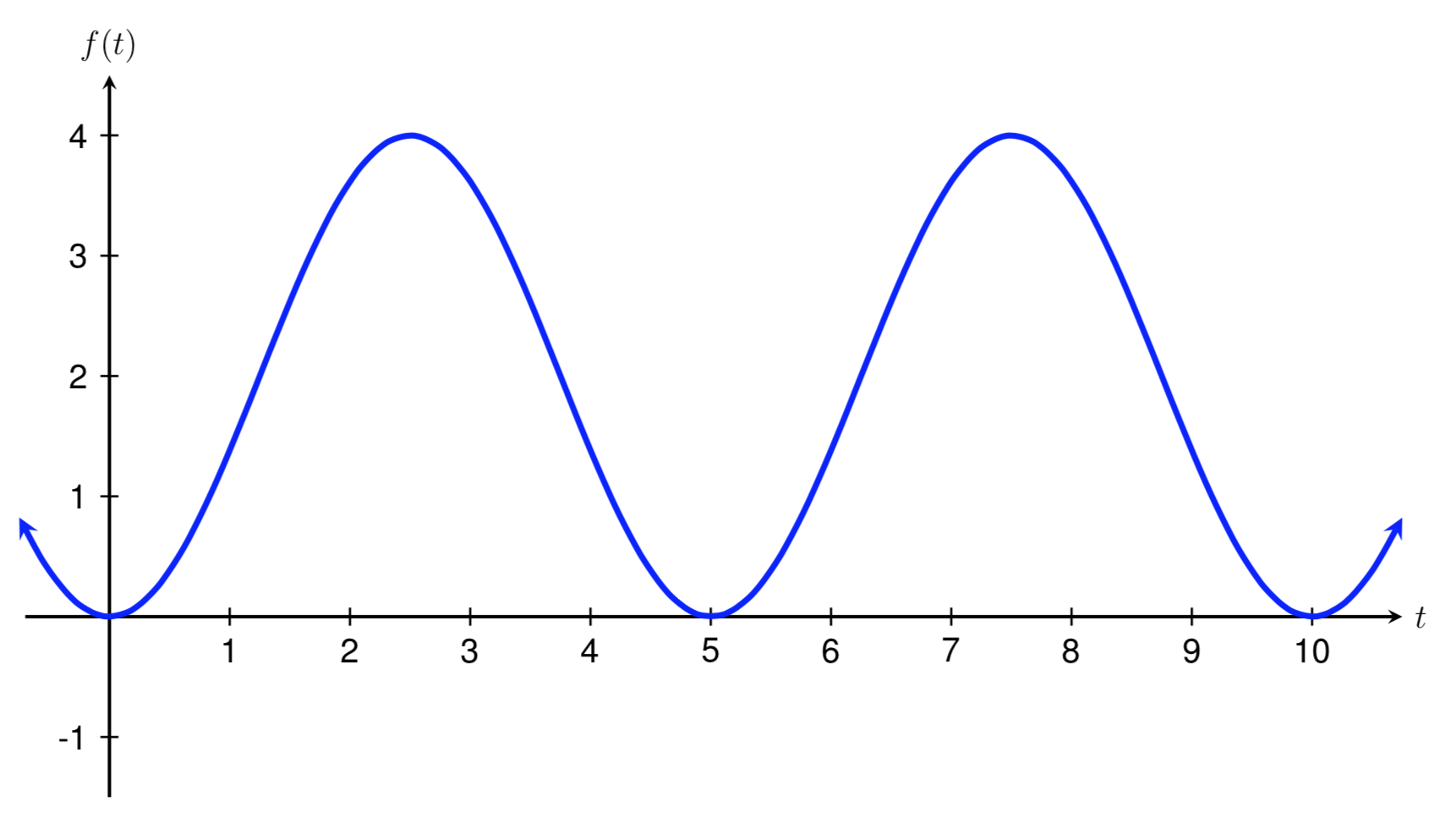
To begin, let's find the period, midline, and amplitude of the function graphed above.
Recall that the period of the function is how long it takes for the function to start repeating. If we think about the function "starting" at \(x=0\text{,}\) or when it crosses the \(y\)-axis, we can see that the function above begins repeating when \(x=5\text{.}\) Therefore, the period of the function graphed above is 5.
Since the period of a function is related to \(B\text{,}\) the stretch/compression factor, we can use the relationship \(P = \frac{2\pi}{|B|}\) to solve for \(B\text{.}\) Substituting 5 in for \(P\text{,}\) we get
\begin{align*}
5 \amp= \frac{2\pi}{|B|} \\
\\
|B| \cdot 5 \amp= 2\pi \\
\\
|B| \amp= \frac{2\pi}{5}
\end{align*}
For now, we can assume that the \(B\) value is positive, which gives us
\begin{equation*}
B = \frac{2\pi}{5}
\end{equation*}
The midline of the function is the horizontal line halfway between the function's maximum and minimum values. Here, the maximum value of the function is 4 and the minimum value is 0. The number halfway between 4 and 0 is 2, so the midline is the line \(y=2\text{.}\) Therefore, the vertical shift of the function graphed above is
\begin{equation*}
k=2
\end{equation*}
Finally, the amplitude of the function is the distance between the function's maximum value and the midline. The distance between the function's maximum value of 4 and the function's midline of \(y=2\) is 2, so the amplitude of the function above is 2. Therefore, the vertical stretch factor is
\begin{equation*}
|A|=2
\end{equation*}
We now need to decide what type of sinusoidal function to use and whether \(A\) is positive or negative. Note that the function shown above crosses the \(y\)-axis at its minimum value. Therefore, from our work above, we need to use a vertical reflection of a cosine graph to model this function, which means that
\begin{equation*}
A=-2
\end{equation*}
Using our work above and substituting our known values into the generalized cosine function \(g(t)=A\cos(Bt) + k\) gives us the following formula for the function graphed above.
\begin{equation*}
f(t) = -2\cos\left(\frac{2\pi}{5}t\right) + 2
\end{equation*}
To check our solution, we can use a graphing calculator to graph the function we came up with and confirm that it matches the graph shown above.