CC Inverse Trigonometric Functions

Subsection3.3Inverse Trigonometric Functions

In the previous subsection, we evaluated trigonometric functions at various angles, but what do we do if we need to know what angle yields a specific sine, cosine, or tangent value? To find angles, we need inverse trigonometric functions.

Intuitively, if \(\sin(\theta)=a\text{,}\) then \(\arcsin(a)=\theta\text{.}\) However, one must be careful about the domain and range of inverse trig formulas to ensure that they are functions.

The Inverse Sine, Inverse Cosine, and Inverse Tangent Functions

For \(a\) in \([-1,1] \text{,}\) \(\arcsin(a)\) is defined to be the unique angle \(\theta\) in \([-\frac{\pi}{2},\frac{\pi}{2}]\) for which \(\sin(\theta)=a\text{.}\)

For \(a\) in \([-1,1]\text{,}\) \(\arccos(a)\) is defined to be the unique angle \(\theta\) in \([0,\pi]\) for which \(\cos(\theta)=a\text{.}\)

For \(a\) in \((-\infty,\infty)\text{,}\) \(\arctan(a)\) is defined to be the unique angle \(\theta\) in \([-\frac{\pi}{2},\frac{\pi}{2}]\) for which \(\tan(\theta)=a\text{.}\)

Note that the output of each of these inverse functions is an angle.

Remark3.37

Do not confuse \(\sin^{-1}(a) \) with \(\frac{1}{\sin(a)}\) as they are not equivalent. The same can be said with \(\cos^{-1}(a) \) and \(\tan^{-1}(a) \text{.}\) As a result, we introduce an alternative (common) notation for the inverse trigonometric functions.

Alternative Notation for the Inverse Sine, Inverse Cosine, and Inverse Tangent Functions

\(\sin^{-1}(a)=\theta\) is equivalent to \(\arcsin(a)=\theta\)

\(\cos^{-1}(a)=\theta\) is equivalent to \(\arccos(a)=\theta\)

\(\tan^{-1}(a)=\theta\) is equivalent to \(\arctan(a)=\theta\)

Example3.38

Find two angles in the interval \([0,2\pi]\) such that \(\displaystyle \sin(\theta)=\frac{1}{2}\text{.}\)

Solution

Since we are given a sine value, we know that we are looking for angles with a \(y\) coordinate of \(\frac{1}{2}\) on the unit circle.

From the common angles on the unit circle, the two angles where \(\sin(\theta)=\frac{1}{2}\) in the interval \([0,2\pi]\) are

\begin{equation*} \theta = \frac{\pi}{6} \hspace{.25in} \text{and} \hspace{.25in} \theta = \frac{5\pi}{6} \end{equation*}

In the previous example, we were able to use the unit circle to solve for \(\theta\text{,}\) but if we are given trigonometric values that do not correspond to common angles on the unit circle, we will need to use a calculator to find approximate values for \(\theta\text{.}\)

Example3.39

Find two angles in the interval \([0,2\pi]\) such that \(\cos(\theta)=-0.4\text{.}\)

Solution

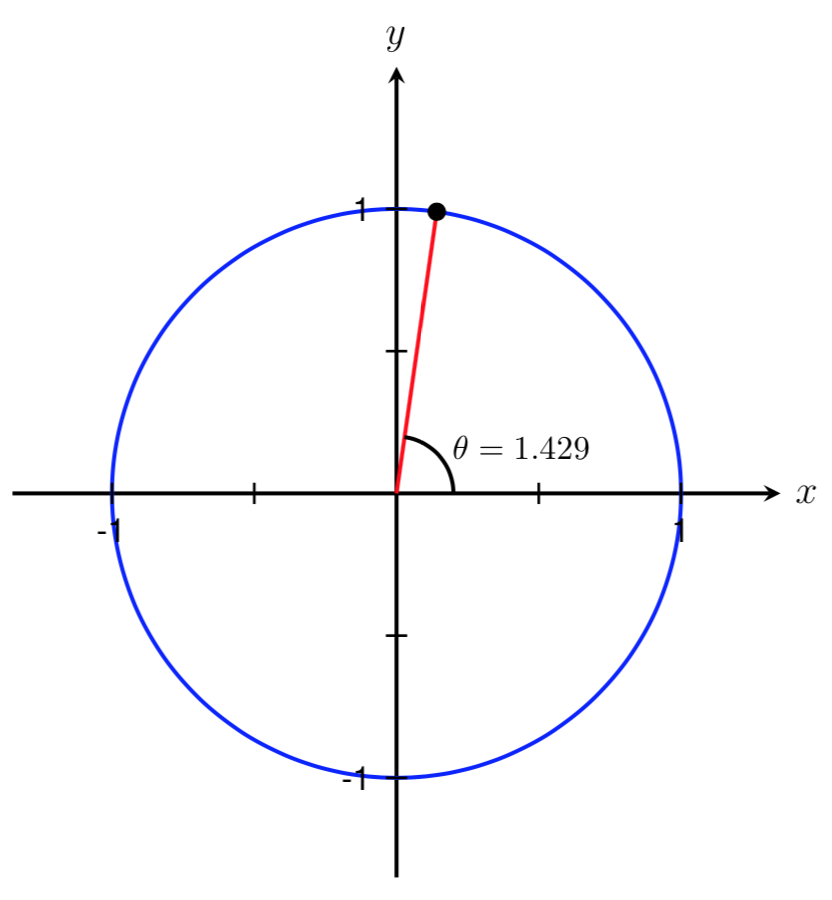
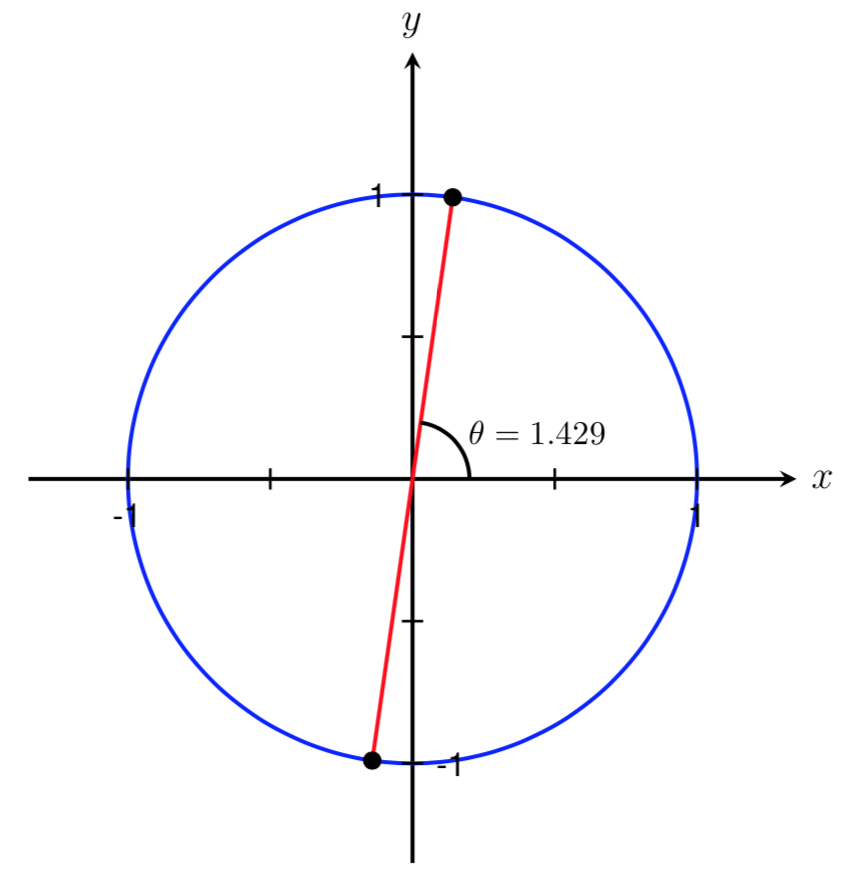
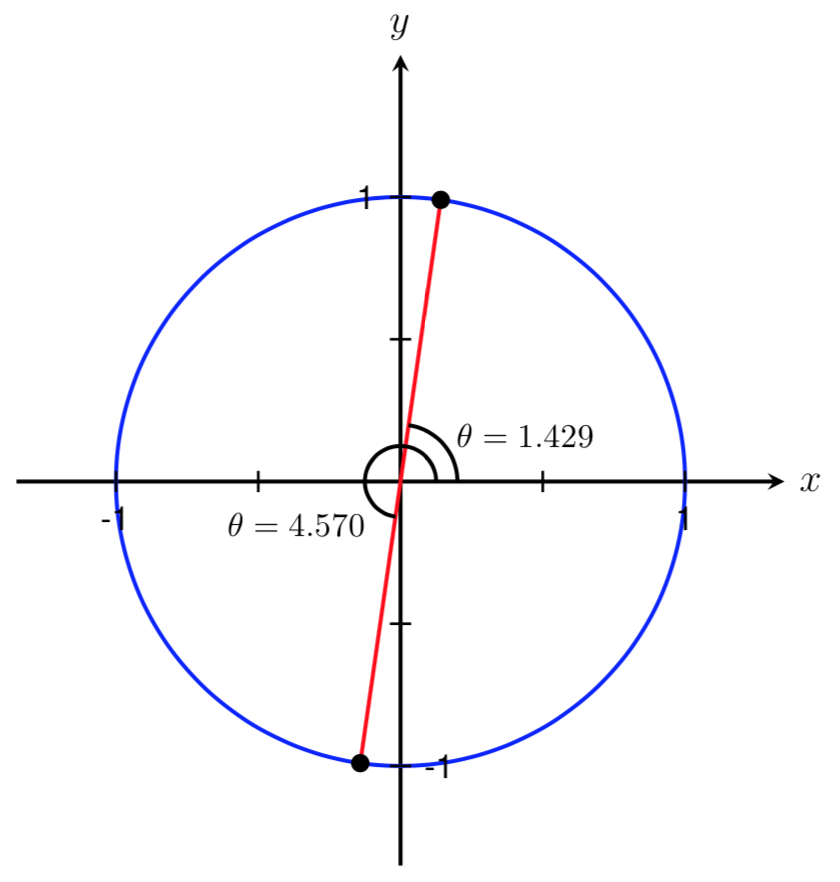
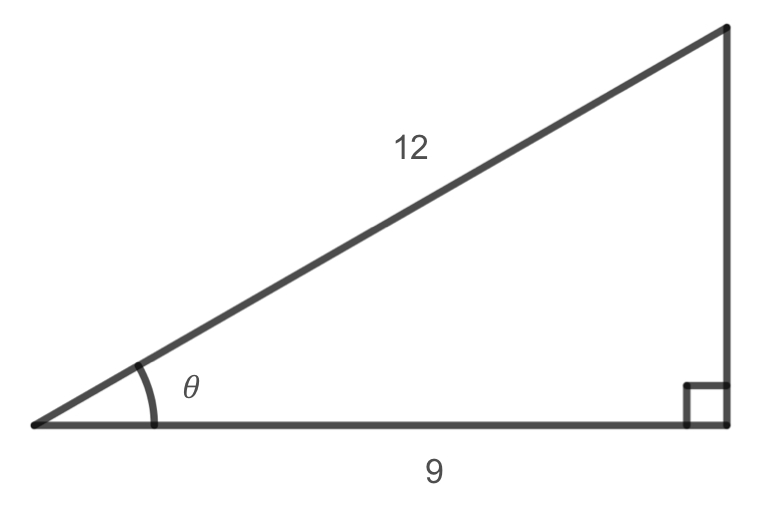
Let's start by drawing a picture and labeling the known information and the angles we are trying to find.

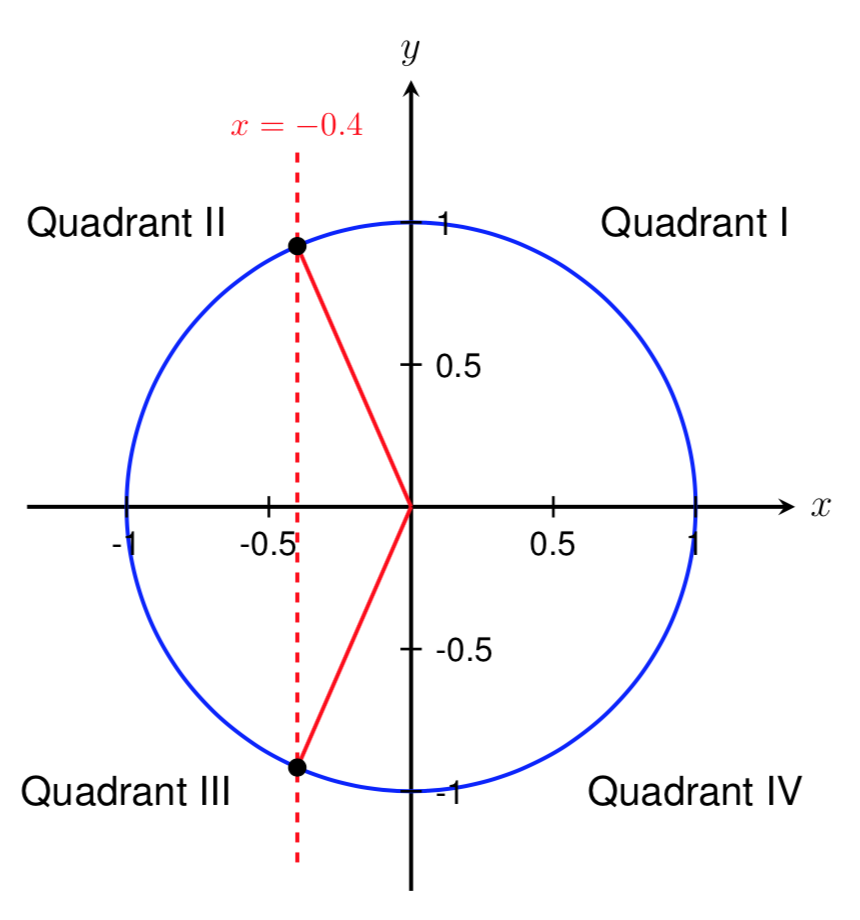
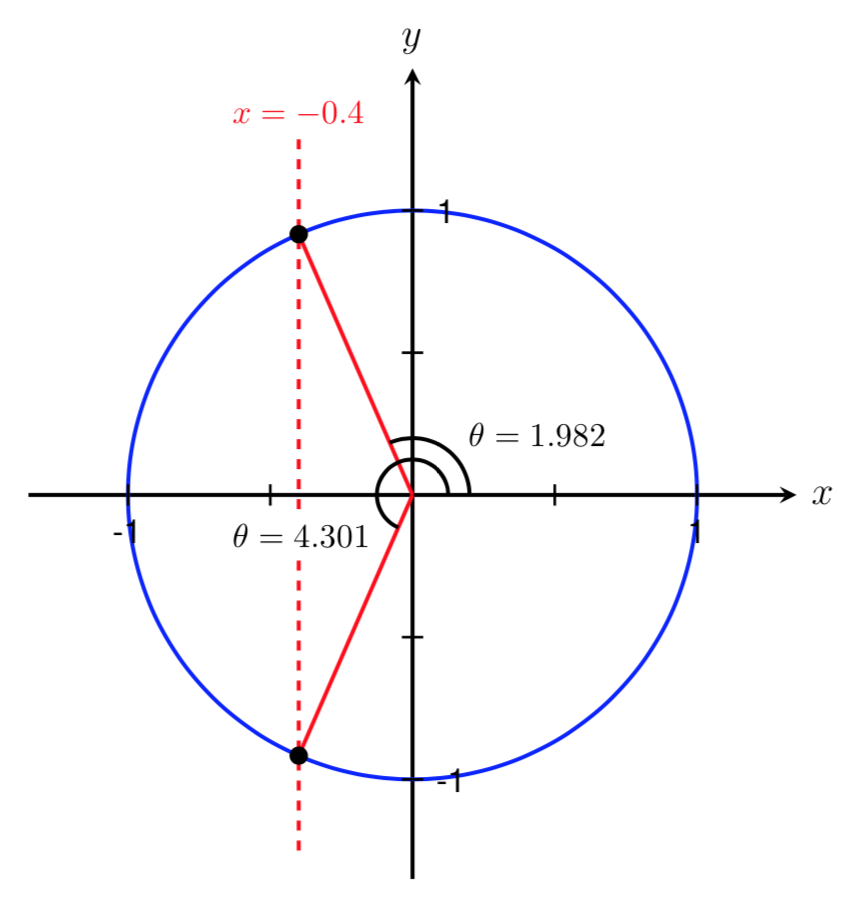
Since we are given a cosine value, we know that we are looking for angles with an \(x\) coordinate of \(-0.4\) on the unit circle. Below is a sketch showing two angles that correspond to \(\cos(\theta) = -0.4\text{.}\) Notice that these two angles lie in Quadrant II and Quadrant III since our cosine value is negative.

Since \(x=-0.4\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse cosine function we get that

\begin{equation*} \theta = \cos^{-1}(-0.4) \end{equation*}

To evaluate this, we can use our calculator. Since the output of the inverse function is an angle, our calculator will give us an angle in degrees if it is in degree mode or an angle in radians if it is in radian mode.

Here, we need to decide whether to provide our answer in degrees or radians. Since we are given the interval \([0,2\pi]\text{,}\) which is radians, we will provide our answers in radians. Using our calculator in radian mode we get that

\begin{equation*} \theta \approx 1.982 \text{ radians} \end{equation*}

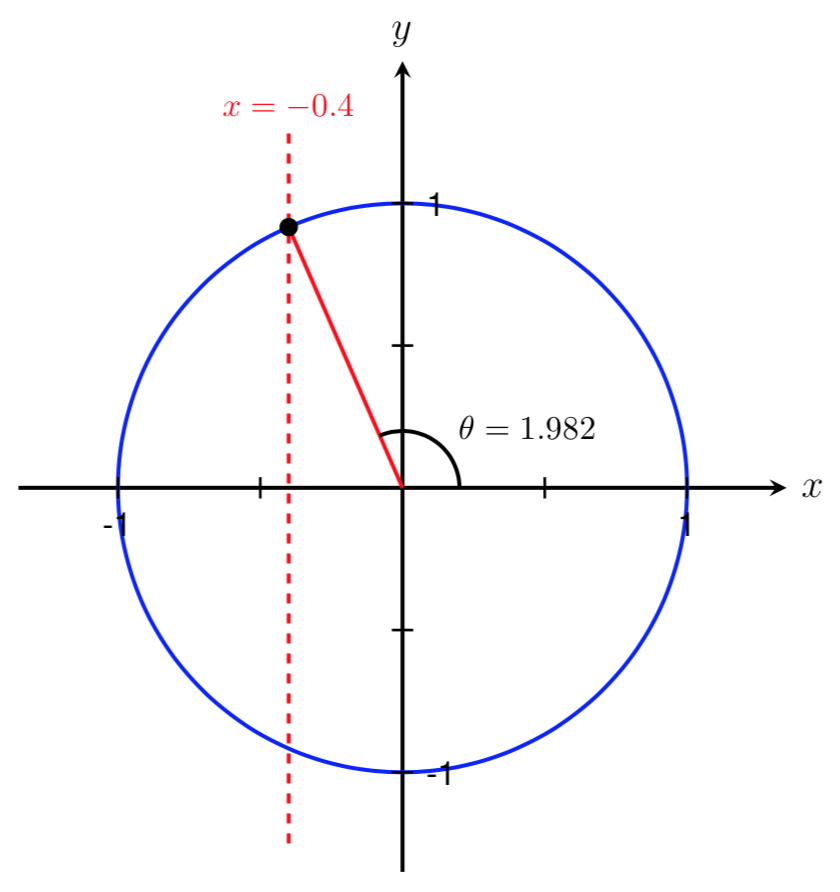
We have now found one angle in the interval \([0,2\pi]\) such that \(\cos(\theta) = -0.4\text{.}\) However, as shown above, \(\theta\) could lie in either Quadrant II or Quadrant III. Since 1.982 is bigger than \(\frac{\pi}{2} \approx 1.571\) and smaller than \(\pi \approx 3.142\text{,}\) we know that \(\theta=1.982\) lies in Quadrant II. Therefore, we have found the angle shown below.

unit circle with cos(theta)=-0.4 and only one angle shown

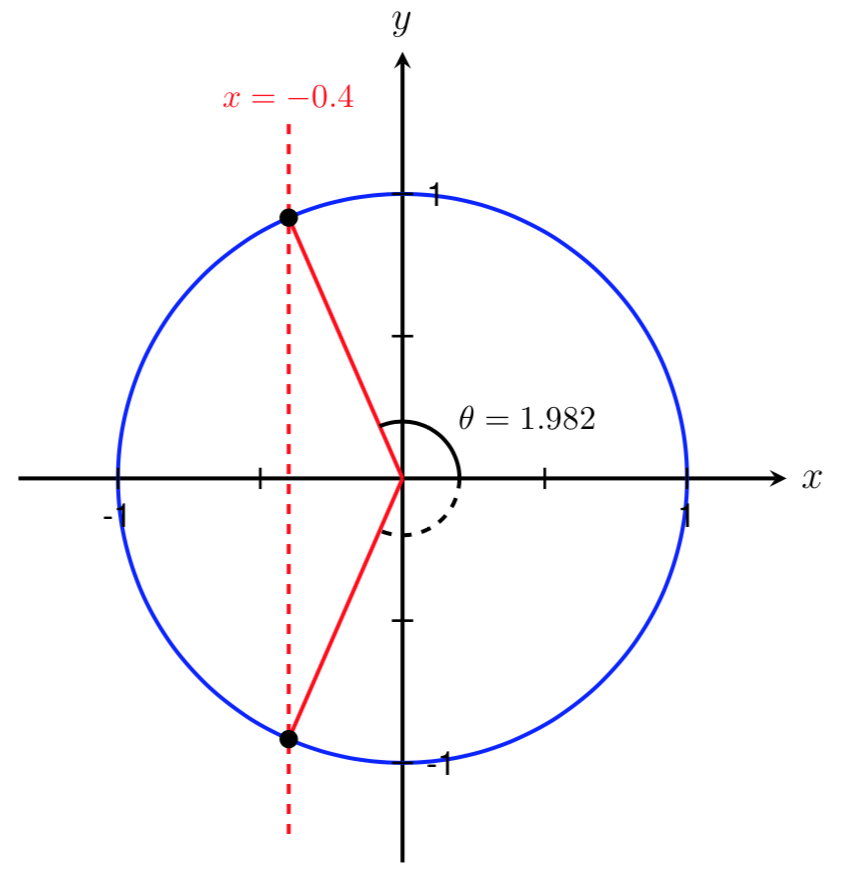
We can now use symmetry to find a second angle in the interval \([0,2\pi]\) such that \(\cos(\theta) = -0.4\text{.}\) We know this angle should be located in Quadrant III. By symmetry, we also know that the two angles shown below are equal.

unit circle with cos(theta)=-0.4 and symmetry of two angles shown

Therefore, to find the second angle, we can take the first angle we found and subtract it from \(2\pi\text{.}\) This gives us an angle of

\begin{equation*} \theta \approx 2\pi - 1.982 \approx 4.301 \text{ radians} \end{equation*}

Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\cos(\theta) = -0.4\) are

\begin{equation*} \theta \approx 1.982 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 4.301 \text{ radians} \end{equation*}

unit circle with cos(theta)=-0.4 and two angles labeled

An easy way to check our solutions is to evaluate \(\cos(1.982)\) and \(\cos(4.301)\) on our calculators. If our calculator returns values close to \(-0.4\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get

\begin{equation*} \cos(1.982)=-0.3997 \hspace{.25in} \text{ and } \hspace{.25in} \cos(4.301)=-0.3999 \end{equation*}

Since both of these values are very close and round to -0.4, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\cos(\theta)=-0.4\text{.}\)

Example3.40

Find all angles in the interval \([0,2\pi]\) such that \(\tan(\theta)=7\text{.}\)

Solution

Since we are given a tangent value, we know that we are looking for angles where \(\frac{y}{x}=7\) on the unit circle. In addition, our tangent value is positive, so this means that \(\theta\) must lie in Quadrant I, where both \(x\) and \(y\) are positive, or in Quadrant III, where both \(x\) and \(y\) are negative.

Since \(\tan(\theta)=7\) does not correspond to a common angle on the unit circle, we need to use a calculator to solve for an approximate value of \(\theta\text{.}\) Applying the inverse tangent function we get that

\begin{equation*} \theta = \tan^{-1}(7) \end{equation*}

Using our calculator in radian mode we get that

\begin{equation*} \theta \approx 1.429 \text{ radians} \end{equation*}

We have now found one angle in the interval \([0,2\pi]\) such that \(\tan(\theta) = 7\text{.}\) However, from our work above, we know that \(\theta\) could lie in either Quadrant I or Quadrant III. Since 1.429 is bigger than 0 and smaller than \(\frac{\pi}{2} \approx 1.571\text{,}\) we know that \(\theta=1.429\) lies in Quadrant I. Therefore, we have found the angle shown below.

unit circle with tan(theta)=7 and only one angle shown

We can now use our knowledge of the tangent function to find a second angle in the interval \([0,2\pi]\) such that \(\tan(\theta) = 7\text{.}\) From our work above, we know this angle should be located in Quadrant III, and we also know that the period of tangent is \(\pi\text{.}\) Therefore, the other angle where \(\tan(\theta)=7\) should be located halfway around the unit circle from our first value.

unit circle with tan(theta)=7 and two angles shown

To find this second angle, we can add \(\pi\) to the first angle we found, which gives us an angle of

\begin{equation*} \theta \approx 1.429 + \pi \approx 4.570 \text{ radians} \end{equation*}

Thus, the two angles in the interval \([0,2\pi]\) that satisfy \(\tan(\theta) = 7\) are

\begin{equation*} \theta \approx 1.429 \text{ radians} \hspace{.25in} \text{ and } \hspace{.25in} \theta \approx 4.570 \text{ radians} \end{equation*}

unit circle with tan(theta)=7 and two angles labeled

Before we move on, let's check our solutions by evaluating \(\tan(1.429)\) and \(\tan(4.570)\) on our calculators. If our calculator returns values close to \(7\text{,}\) then we know the angles we have found are correct. Using our calculator (in radian mode), we get

\begin{equation*} \tan(1.429)=7.005 \hspace{.25in} \text{ and } \hspace{.25in} \tan(4.570)=6.975 \end{equation*}

Since both of these values are very close to 7, we can be confident that we have found the two angles in the interval \([0,2\pi]\) that satisfy \(\tan(\theta)=7\text{.}\)

Using inverse trig functions, we can also solve for the angles of a right triangle given two of its sides.

Example3.41

Solve the triangle for the angle \(\theta\text{.}\)

right triangle with hypotenuse and adjacent side labeled

Solution

Since we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.

\begin{align*} \cos(\theta) \amp = \frac{9}{12} \amp\amp\text{Using the definition of the inverse} \\ \\ \theta \amp = \cos^{-1}\left(\frac{9}{12}\right) \amp\amp\text{Evaluating on our calculator} \\ \\ \theta \amp \approx 0.723 \text{ radians} \amp\amp\text{or about } \ 41.410^\circ \end{align*}

right triangle with hypotenuse, adjacent side, and angle labeled

Note3.42Common Notation for the Inverse Trigonometric Functions

The inverse sine function, \(\sin^{-1}(a)\) is sometimes called the arcsine function, and notated \(\arcsin(a)\text{.}\)

The inverse cosine function, \(\cos^{-1}(a)\) is sometimes called the arccosine function, and notated \(\arccos(a)\text{.}\)

The inverse tangent function, \(\tan^{-1}(a)\) is sometimes called the arctangent function, and notated \(\arctan(a)\text{.}\)