Linear Equation
A linear function is a function which has a constant rate of change.
Subsection1.7Linear Functions
Linear relationships are relationships in which the rate of change is constant.
\begin{equation*}
f (x) = (\text{starting value}) + (\text{rate of change}) \cdot x.
\end{equation*}
The initial value, or the value of \(f(0)\text{,}\) is the vertical intercept of the graph, and the rate of change is the slope of the graph. Thus, we can write an equation of a line as
\begin{equation*}
f (x) = b + mx
\end{equation*}
where the constant term, \((0,b)\text{,}\) is the vertical intercept of the line, and \(m\text{,}\) the coefficient of \(x\text{,}\) is the slope of the line. This form for an equation of a line is called the slope-intercept form.
Slope-Intercept Form
If we write an equation of a linear function in the form,
\begin{equation*}
f (x) = mx + b
\end{equation*}
then \(m\) is the slope of the line, and \((0,b)\) is the vertical intercept although we frequently refer to the intercept by the value \(b\) since the other coordinate is always \(0\text{.}\)
Example1.14
An icicle grows according to the formula \(H(t)=0.05t+0.12\text{,}\) where \(t\) is the time in minutes since the first measurement was take, and \(H(t)\) is the height of the icicle in centimeters.
The slope is 0.05, which tells us that the icicle's height grows by 0.05 cm each minute.
The \(y\)-intercept is 0.12, which tells us that the height of the icicle was 0.12 cm at the first measurement.
Example1.15
Samantha owns a catering business. For any party with up to 100 guests, she charges \(\$ 2,000\text{.}\) She charges \(\$ 8\) per person for each additional guest over 100. Give a formula for the cost of having Samantha cater your party as a function of the number of guests over 200.
Solution
A possible formula for the cost of having Samantha cater your party is \(C(g)=2000+8g\text{,}\) where \(g\) is the number of guests over 100.
The following formula provides a method for finding the value of the slope \(m\) when given two points on the line.
Two-Point Slope Formula
The slope of the line passing through the points \(P_1 (x_1, y_1)\) and \(P_2 (x_2, y_2)\) is given by
\begin{equation*}
m = \frac{\Delta y}{\Delta x}= \frac{y_2 - y_1}{x_2 - x_1}
\text{, }~x_2 \ne x_1.
\end{equation*}
Example1.16
Compute the slope of the line between the points \((6, -3)\) and \((4, 3)\text{.}\)
Solution
Substitute the coordinates of \(Q_1\) and \(Q_2\) into the slope formula to find
\begin{equation*}
m = \frac{y_2 - y_1}{x_2 - x_1}= \frac{3 - (-3)}{4 - 6}
= \frac{6}{-2}= -3.
\end{equation*}
This value for the slope, \(-3\text{,}\) is the same value found above.
Sometimes you will be given the slope of a line and another point on that line. The following formula is helpful in that situation.
Point-Slope Form
An equation of the line that passes through the point \((x_1, y_1)\) and has slope \(m\) is
\begin{equation*}
y- y_1= + m(x- x_1).
\end{equation*}
Example1.17
Find a formula for the line that has slope -2 and passes through the point \((-1,4)\text{.}\)
Solution
Using point-slope form, we have the line \(y=4+(-2)(x-(-1))\text{.}\)
We can also write this in slope-intercept form by simplifying: \(y=2-2x\text{.}\)
Is is also useful to introduce the term \(x\)-intercept. An \(x\)-intercept for a function \(f(x)\) is the value of \(x\) such that \(f(x)=0\text{.}\)\(x\)-intercept
Note1.18
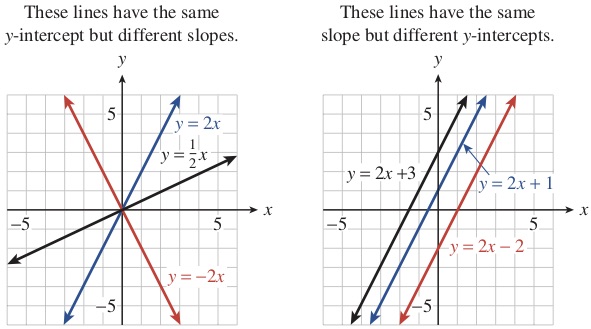
In the equation \(f (x) = mx + b\text{,}\) we call \(m\) and \(b\) parameters. Their values are fixed for any particular linear equation; for example, in the equation \(y = 2x + 3\text{,}\) \(m = 2\) and \(b = 3\text{,}\) and the variables are \(x\) and \(y\text{.}\) By changing the values of \(m\) and \(b\text{,}\) we can write the equation for any line except a vertical line (see Figure1.19). The collection of all linear functions \(f (x) = mx + b\) is called a two-parameter family of functions.
